전 시간에 배운 평행선 사이의 선분의 길이의 비는 중학교 기하에서 가장 중요한 비례 개념 중 하나입니다. 특히 사다리꼴과 평행한 직선이 포함된 문제에서 평행선과 선분의 길이의 비를 응용하면 복잡한 길이 계산도 간단하게 해결할 수 있습니다.
이 글에서는 평행선과 선분의 길이의 비를 활용하는 대표적인 응용 문제를 중심으로, 사다리꼴과 세 평행선에서의 선분의 길이비를 두 가지 풀이를 이용해 단계별로 정리했습니다.
평행선 사이의 선분의 길이의 비 응용
응용1 사다리꼴
먼저 사다리꼴에서 적용할 수 있는 평행한 직선과 선분의 길이 사이의 관계에 대하여 살펴보도록 합시다.
$\overline{AD}\pa\overline{BC}$인 사다리꼴 $\triangle ABCD$에서 $\overline{EF}\pa\overline{BC}$일 때, $\overline{EF}$의 길이를 구하는 두 가지 방법에 대해 정리해 보겠습니다.
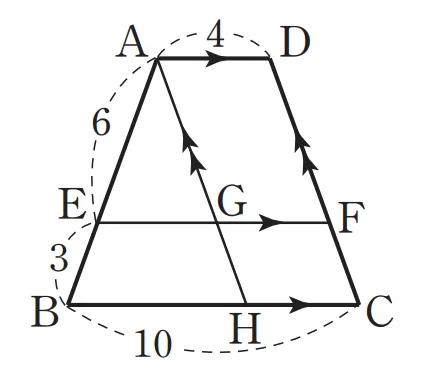
풀이
$\overline{GF}=\overline{HC}=4$이고 $\triangle{AEG} \sm \triangle ABH$ (AA 닮음)이므로 $\overline{AE}:\overline{AB}$$=\overline{EG}:\overline{BH}$
$6:9=\overline{EG}:6$
따라서 $\overline{EG}=4$이고, $\overline{EF}=8$이다.
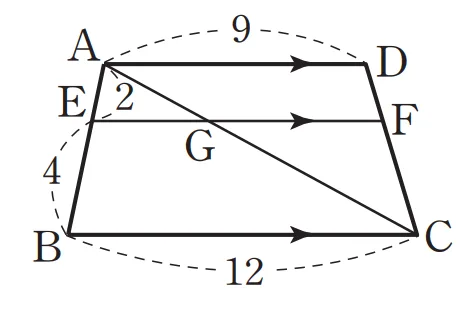
풀이
$\triangle{AEG} \sm \triangle ABH$ (AA 닮음)이므로
$\overline{AE}:\overline{AB}$$=\overline{EG}:\overline{BC}$
$2:6=\overline{EG}:12$이고, $\overline{EG}=4$이다.
$\triangle{CGF} \sm \triangle {CAD}$ (AA 닮음)이므로
$\overline{CF}:\overline{CD}$$(=\overline{BE}:\overline{BA})$$=\overline{GF}:\overline{AD}$
$4:6=\overline{FG}:9$, $\overline{FG}=6$이다.
따라서 $\overline{EF}= \overline{EG} +\overline{FG} =10$
위의 예시를 통해 평행선과 선분의 길이의 비에서 사다리꼴 응용에 대해 다음과 같이 일반화 시켜 정리할 수 있습니다.
$\overline{AD}\pa\overline{BC}$인 사다리꼴 $\triangle ABCD$에 $\overline{EF}\pa\overline{BC}$일 때, $\overline{EF}$의 길이를 구하는 두 가지 방법
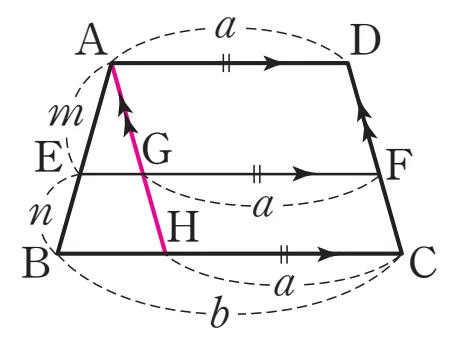
[방법 1] 평행선 이용
$\triangle ABH$에서 $\overline{EG} : \overline{BH} = m : (m+n)$이고 $\overline{EG}(m+n)=(b-a)m$이므로 $\overline{EG}=\dfrac{(b-a)m}{m+n}$
평행사변형 $AHCD$에서 $\overline{GF} = \overline{HC} = \overline{AD} = a$
$\therefore \overline{EF} = \overline{EG} + \overline{GF}$
$\overline{EF} = \dfrac{a n + b m}{m + n}$
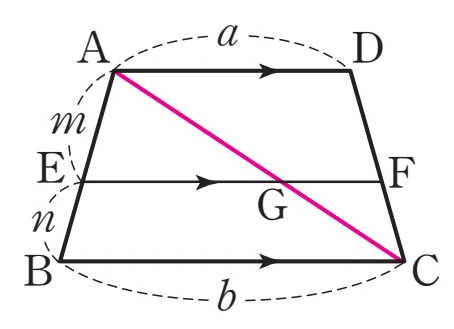
[방법 2] 대각선 이용
$\triangle ABC$에서 $\overline{EG} : \overline{BC} = m : (m+n)$이고 $\overline{EG}=\dfrac{bm}{m+n}$
$\triangle ACD$에서 $\overline{GF} : \overline{AD} = n : (m+n)$이고 $\overline{GF}=\dfrac{an}{m+n}$
$\therefore \overline{EF} = \overline{EG} + \overline{GF}$이고,
$\overline{EF} = \dfrac{a n + b m}{m + n}$이다.
응용2 평행한 세 직선
평행한 세 직선과 선분의 길이의 비에 대하여 살펴보도록 하겠습니다.
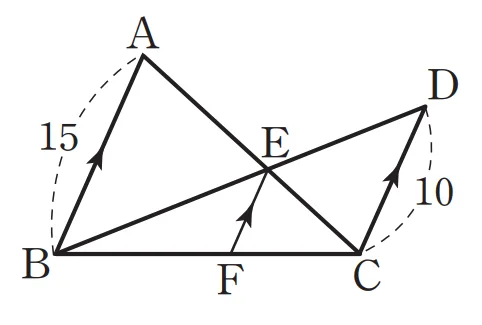
$\overline{AB}\pa\overline{EF}\pa\overline{DC}$일 때, $\overline{EF}$의 길이를 구하는 방법은 다음과 같습니다.
방법1
$\triangle EAB \sm \triangle ECD$ AA닮음, 닮음비 $15:10=3:2$
$\triangle ABC \bbox[#ffff00]{\sm} \triangle EFC$ AA닮음, 닮음비가 $2:5$이므로
$2:5=\overline{EF}:15$, $\overline{EF}=6$이다.
방법2
$\triangle EAB \sm \triangle ECD$ AA닮음, 닮음비 $15:10=3:2$
$\triangle DBC \bbox[#dcff8d]{\sm} \triangle EBF$ AA닮음, 닮음비가 $3:5$이므로
$3:5=\overline{EF}:10$, $\overline{EF}=6$이다.
평행한 세 직선과 선분의 길이의 비에 대한 두 가지 풀이를 일반화 시키면 아래와 같이 정리할 수 있습니다.
$\overline{AB}\pa\overline{EF}\pa\overline{DC}$일 때, $\overline{EF}$의 길이를 구하는 두 가지 방법
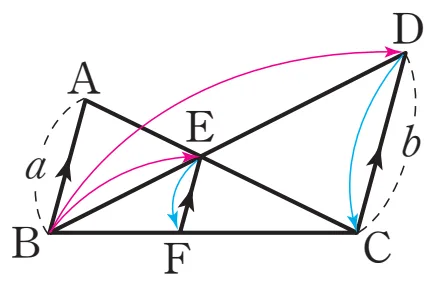
[방법 1]
$\triangle EAB \sm \triangle ECD$ 닮음비가 $a:b$인 AA닮음
$\overline{BE} : \overline{BD} = \overline{EF} : \overline{DC}$
$a : (a+b) = \overline{EF} : b$
$\therefore \overline{EF} = \dfrac{ab}{a+b}$
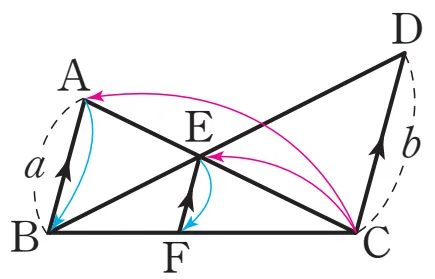
[방법 2]
$\triangle EAB \sm \triangle ECD$ 닮음비가 $a:b$인 AA닮음
$\overline{CE} : \overline{CA} = \overline{EF} : \overline{AB}$
$b : (b+a) = \overline{EF} : a$
$\therefore \overline{EF} = \dfrac{ab}{a+b}$
[출처: 개념원리]
