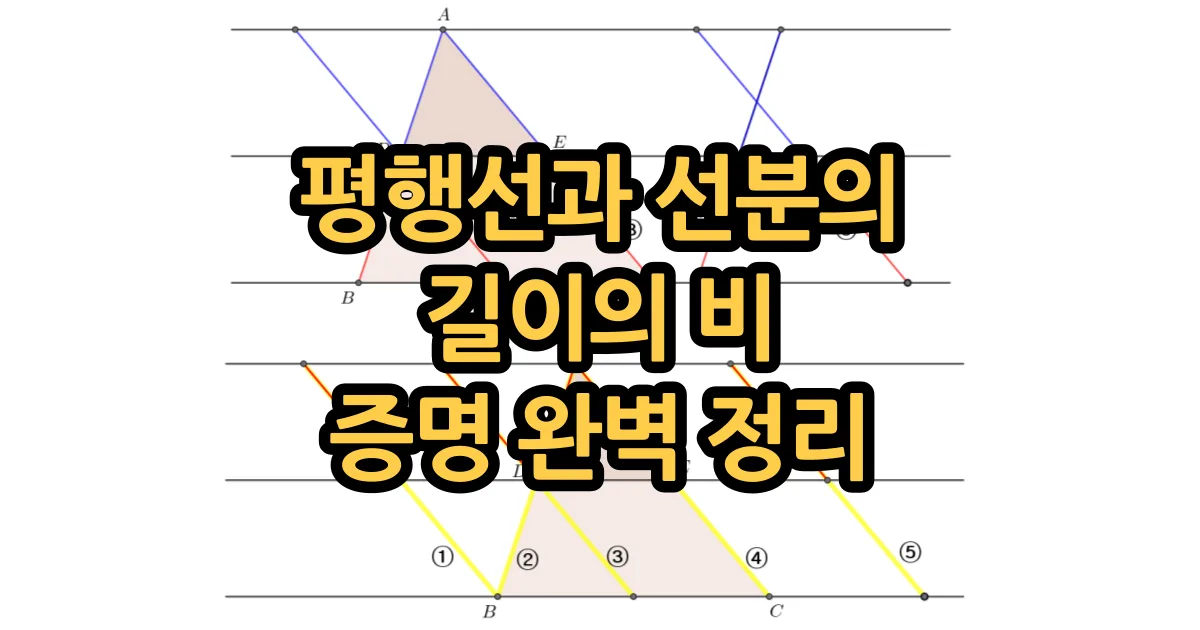
평행선과 선분의 길이비는 중학교 도형 단원에서 닮음과 비례의 핵심 개념을 이해하기 위한 중요한 내용입니다. 두 직선이 평행할 때 성립하는 성질뿐 아니라, 일정한 길이비가 주어졌을 때 두 직선이 평행임을 판정할 수 있는 조건으로도 활용됩니다. 이 글에서는 $\triangle ABC$에서 평행선의 성질과 조건을 증명과 함께 단계별로 정리하고, 이를 확장하여 다양한 형태의 평행선과 선분의 길이의 비를 탐구해 보겠습니다.
목차
평행선과 선분의 길이비1
평행선과 선분의 길이의 비에 대한 내용은 평행할 때 성립하는 성질임과 동시에 두 직선에 의해 잘린 비율이 일정하면 두 직선이 평행하다고 결정할 수 있는 조건이 되기도 합니다. 따라서 다음과 같이 각각 성질과 조건으로 정리하는 것이 좋습니다.
$\triangle ABC$에서 두 변 $AB$, $AC$ 또는 그 연장선 위에 각각 점 $D$, $E$가 있을 때
- 평행선의 성질
$\overline{BC}⫽\overline{DE}$ $\Rightarrow$ $\overline{AB} : \overline{AD} = \overline{AC} : \overline{AE} = \overline{BC} : \overline{DE}$ - 평행선의 조건
$\overline{AB} : \overline{AD} = \overline{AC} : \overline{AE} = \overline{BC} : \overline{DE}$ $\Rightarrow$ $\overline{BC}⫽\overline{DE}$
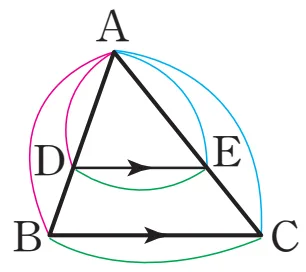
[성질 증명]
$\overline{BC}⫽\overline{DE}$이면 $\triangle ABC$와 $\triangle ADE$에서
$\angle ABC = \angle ADE$ (동위각), $\angle A$는 공통
따라서 $\triangle ABC \sim \triangle ADE$ (AA 닮음)
$\therefore \overline{AB} : \overline{AD} = \overline{AC} : \overline{AE} = \overline{BC} : \overline{DE}$
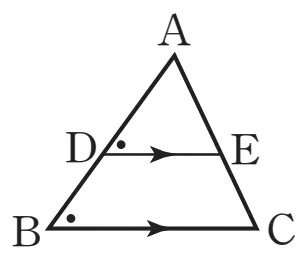
[조건증명]
$\overline{AB} : \overline{AD} = \overline{AC} : \overline{AE}$, $\angle A$는 공통
따라서 $\triangle ABC \sim \triangle ADE$ (SAS 닮음)
$\therefore \angle ABC = \angle ADE$에서 동위각의 크기가 같으므로 $\overline{BC}⫽\overline{DE}$
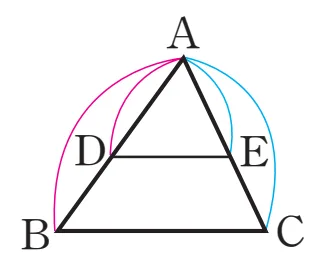
확장
위의 성질에서 변의 길이비가 같은 부분을 같은 색으로 나타내고, 평행선 사이의 선분 $\overline{AC}$를 평행하게 이동하면 선분의 길이비를 더 다양하게 생각해 볼 수 있습니다.
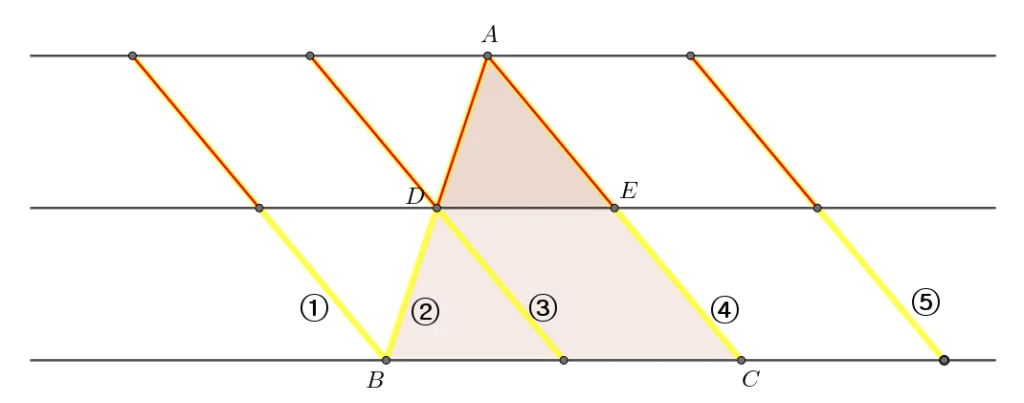
$\overline{AC}$의 위치에 따라서 평행선 사이의 선분의 길이비를 정리하면 아래와 같습니다.
[1+2]
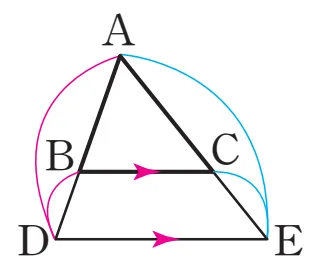
$\overline{DB}:\overline{DA}$$=\overline{EC}:\overline{EA}$
[2+3]
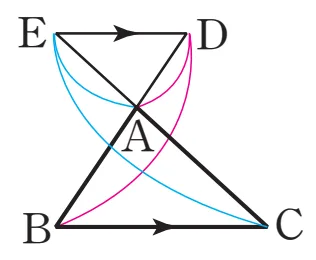
$\overline{DA}:\overline{DB}$$=\overline{EA}:\overline{EC}$
[2+5]
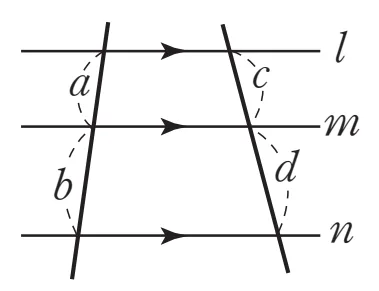
$a:a+b$$=c:c+d$
평행선과 선분의 길이비2
이번에는 다른 관점에서 평행한 두 직선 사이의 선분의 길이비를 평행선의 성질과 조건으로 나누어 정리해 보겠습니다.
- 평행선의 성질: $\overline{BC}⫽\overline{DE}$이면 $\overline{AD} : \overline{DB} = \overline{AE} : \overline{EC}$
- 평행선의 조건: $\overline{AD} : \overline{DB} = \overline{AE} : \overline{EC}$이면 $\overline{BC}⫽\overline{DE}$
- 오개념 주의
$\overline{AD} : \overline{DB} \neq \overline{DE} : \overline{BC}$
위의 성질과 조건에 대한 증명은 아래와 같습니다.
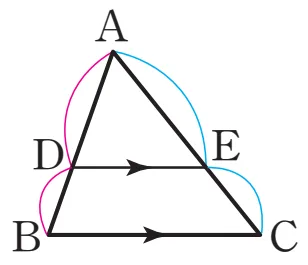
[성질 증명]
$\overline{AB}⫽\overline{EF}$가 되도록 $\overline{BC}$ 위에 점 $F$를 잡으면, $\triangle ADE$와 $\triangle EFC$에서
$\angle DAE = \angle FEC$ (동위각), $\angle AED = \angle ECF$ (동위각)
따라서 $\triangle ADE \sim \triangle EFC$ (AA 닮음)
$\overline{AD} : \overline{EF} = \overline{AE} : \overline{EC}$이고 $\overline{DB} = \overline{EF}$이므로
$\overline{AD} : \overline{DB} = \overline{AE} : \overline{EC}$
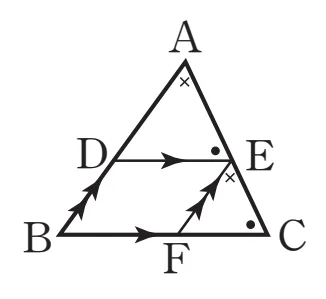
[조건 증명]
$\overline{AD} : \overline{DB} = \overline{AE} : \overline{EC}$일 때 $\overline{BD}$와 평행하고 $E$를 지나는 직선과 $\overline{BC}$가 만나는 점 $F$에 대하여 $\triangle ADE \sim \triangle EFC$입니다.
- $\overline{AD} : \overline{DB} = \overline{AE} : \overline{EC}$
- $\angle{DAE}=\angle{FEC}$ 동위각
두 닮은 도형의 대응각으로 $\angle{AED}=\angle{ECF}$이고 따라서 $\overline{DE} ⫽ \overline{BC}$ 입니다.
확장
$\overline{AB}$와 $\overline{AC}$를 평행하게 이동하면 평행선 사이의 선분의 길이비를 더 다양하게 생각해 볼 수 있습니다.
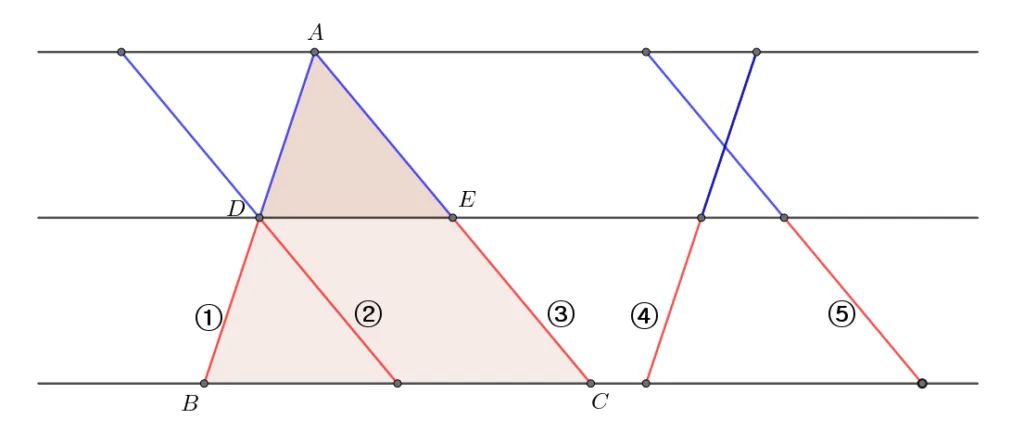
$\overline{AB}$와 $\overline{AC}$의 위치에 따라서 평행선 사이의 선분의 길이비를 정리하면 아래와 같습니다.
[1+2]
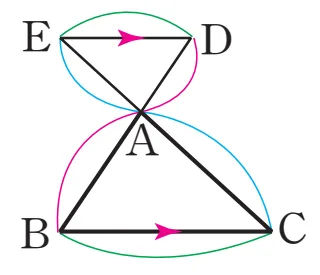
$\overline{AD}:\overline{AB}$$=\overline{AE}:\overline{AC}$
[1+5]
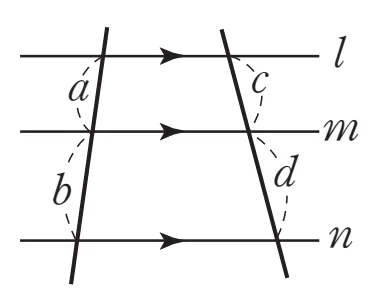
$a:b$$=c:d$
[4+5]
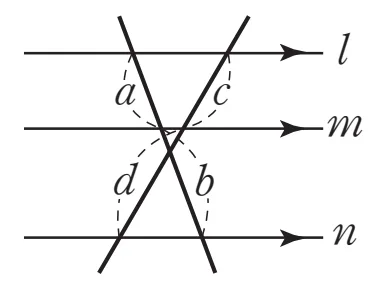
$a:b$$=c:d$
출처: 개념원리