직선 반직선 선분에 대해 정확히 이해하는 것은 기하학을 학습하는데 필수적입니다. 이 글에서는 직선, 반직선, 선분의 정의와 기호에 대해 학습하고, 이들 사이의 차이점에 대해 정리하였습니다. 또한 직선을 결정하는 조건, 두 점 사이의 거리, 선분의 중점에 대해 중학교 수학 수준에서 쉽게 이해할 수 있도록 설명하였습니다.
목차
직선 반직선 선분
직선과 선분은 일상에서 비슷한 의미로 사용하지만 수학에서는 서로 다른 의미로 다음과 같이 엄밀하게 정의하여 사용한다.
직선 반직선 선분은 다음과 같이 직관적으로 표현하고 의미는 아래와 같다.
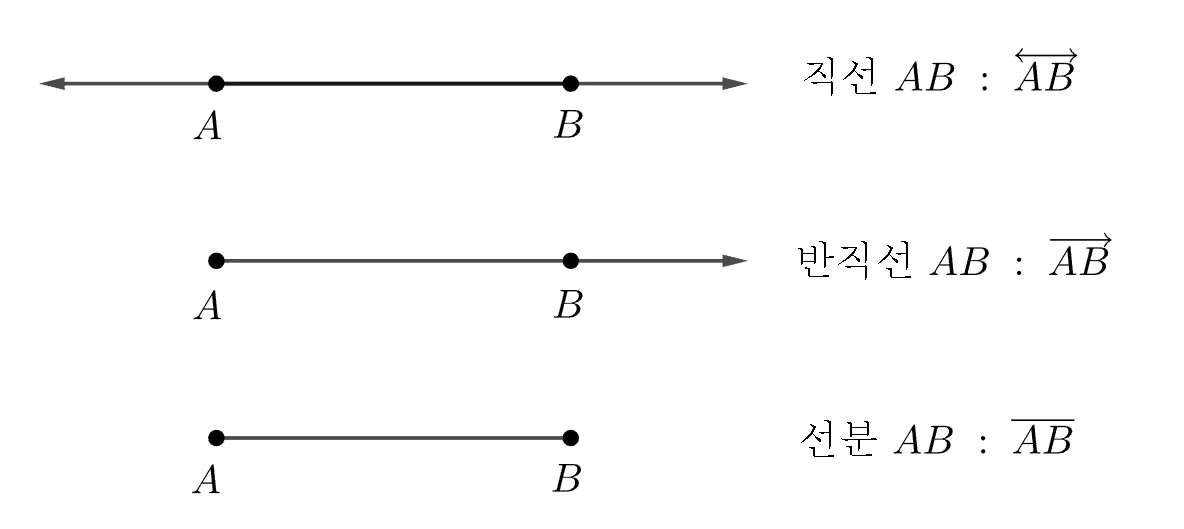
- 직선 AB
- 서로 다른 두 점 A, B를 지나 양쪽으로 무한히 길게 뻗은 선
- 기호: $\overleftrightarrow{AB}$
- 반직선 AB
- 점 A에서 시작하여 점 B방향으로 무한히 길게 뻗은 직선의 일부
- 기호: $\overrightarrow{AB}$
- 선분 AB
- 두 점 A, B와 그 사이를 연결하는 직선의 일부
- 기호: $\overline{AB}$
기호 사용시 주의 사항
직선과 선분은 양쪽 점에서 선의 모양이 대칭이므로 문자를 바꾸어 적는 것이 가능하다.
- $\overleftrightarrow{AB}=\overleftrightarrow{BA}$
- $\overline{AB}=\overline{BA}$
반면에 반직선의 경우 두 점에서 선의 구조가 대칭이 아니기 때문에 다음과 같이 표현할 수 없다.
- $\overrightarrow{AB}\neq\overrightarrow{BA}$
위의 기호가 각각 의미하는 반직선은 아래와 같고 따라서 둘은 서로 다르다.
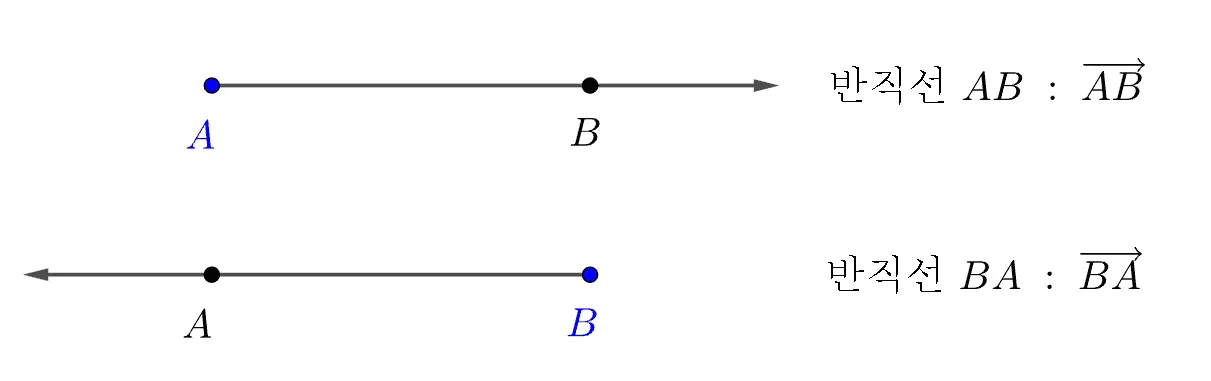
그리고 위의 그림에서 반직선 BA를 왼쪽 화살표를 이용해 다음과 같은 기호로 표현하지 않음에 주의하자.
- $\overleftarrow{AB} \;\;\times $ : 왼쪽 화살표는 사용하지 않음
직선의 결정조건
이제 직선이 하나로 결정될 조건에 대해 생각해 보자. 먼저 한 점을 지나는 직선의 개수는 몇 개나 있지 생각해 보고 직선의 결정조건에 대해 정리해 보자.
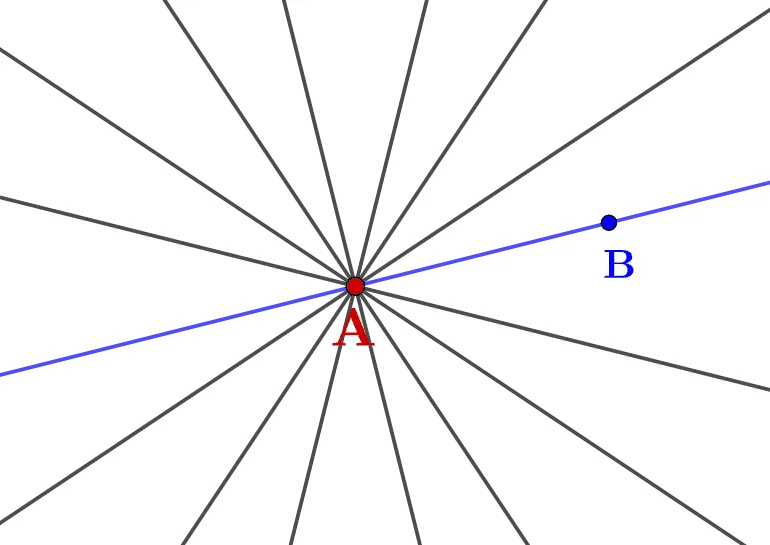
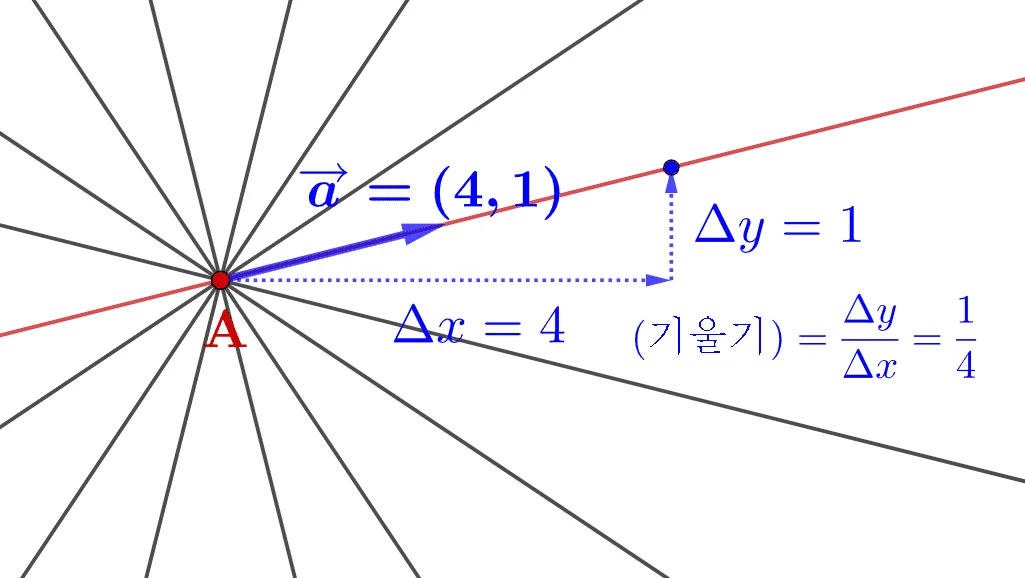
위의 그림을 통해 알 수 있듯이 한 점A를 지나는 직선은 무수히 많다. 따라서 점A를 지나는 직선 중 파란색 직선으로 결정하기 위해서는 다음과 같은 조건이 필요하다.
- 점 $\color{#dc143c}{A}$와 $\color{#0000ff}{B}$를 지나는 직선(중1)
또 다른 방법으로는 한 점과 직선의 방향을 표현하는 수학적 요소를 이용하는 방법이 있다. 직선의 방향은 평행한 직선(중1), 기울기(중2), 벡터(고등)로 주어질 수 있다.
직선의 결정조건을 간단히 정리해 보면 다음과 같다.
- 다음이 주어지면 직선은 하나로 결정된다.
- 서로 다른 두 점
- 한 점과 직선의 방향(평행한 직선, 기울기, 벡터)
거리
직선과 반직선은 끊임없이 뻗어 나가는 선이므로 길이나 거리를 논할 수 없다. 하지만 선분의 경우 양끝점을 지나서 계속 뻗어나가지 않으므로 길이를 잴 수 있다. 두 점 사이의 거리에 대한 수학적 개념을 이해하고 선분의 개념과 연결지어 보자.
두 점 사이의 거리
일상에서 거리는 대부분 이동거리를 의미한다. 하지만 수학에서 거리는$\bbox[#ffc5fd]{\text{최단거리}}$를 의미한다. 아래의 그림을 통해$\bbox[#ffff00]{\text{두 점사이의 거리}}$에 대해 학습해 보자.
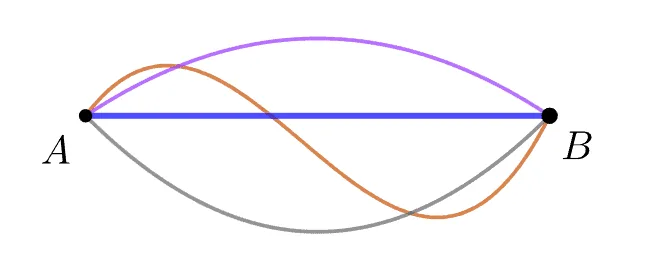
두 점 $A,\;B$사이의 거리
- $\overline{AB}$의 길이
- 기호 : $\overline{AB}$
참고로 선분 AB자체를 표기하는 기호와 선분 AB의 길이를 표기하는 기호는 $\overline{AB}$로 동일하다.
중점
$\bbox[#ffff00]{\text{선분 AB의 중점}}$을 $\bbox[#ffff00]{\text{두 점 A, B의 중점}}$ 이라고도 하고 다음과 같이 정의한다.
- 선분 AB의 한 가운데 있는 점
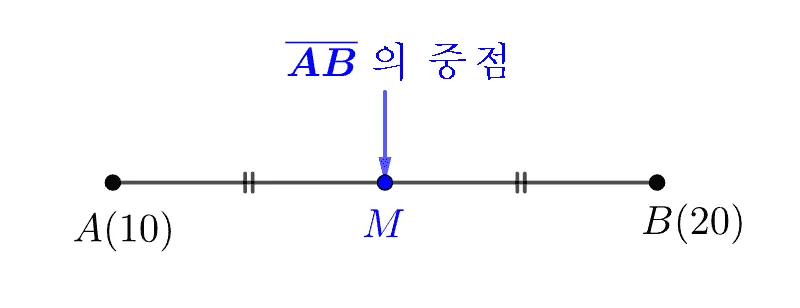
중점은 $M$(Mid point)으로 표기하고 정의에 의해 $\overline{AM}=\overline{BM}$이고 각 각은 $\overline{AB}$길이의 절반이므로 다음과 같이 정리할 수 있다.
- $\dfrac{1}{2}\overline{AB}=\overline{AM}=\overline{BM}$
위의 그림에서 처럼 중점의 좌표가 $A(10)$, $B(20)$으로 주어지면 중점 $M(x)$의 좌표는 다음과 같이 구할 수 있다.
$\begin{align}x&=(\text{A좌표})+\dfrac{\overline{AB}}{2}\\[1em]
&=10+\dfrac{20-10}{2}\\[1em]
&=10+5\\[1em]
&=15\end{align}$
이를 일반화 하여 정리하면 다음과 같다.
중점의 좌표
먼저 결과부터 정리하고 증명에 대해 정리해 보도록 하자.
- 두 점 $A(a),\; B(b)$의 중점 $M$의 좌표는 다음과 같다.
- $M\left( \dfrac{a+b}{2} \right)$
여기서는 $a<b$에 대해서만 증명하고 $b<a$의 경우는 학생들에게 맡기도록 하겠다.
$a<b$이면 $\overline{AB}=b-a$이고 중점은 $A(a)$보다 오른쪽으로 $\dfrac{\overline{AB}}{2}$만큼 떨어진 곳에 있다. 따라서 중점$M(x)$의 좌표는 다음과 같다.
$\begin{align}x&=a+\dfrac{\overline{AB}}{2}\\[1em]
&=a+\dfrac{b-a}{2}\\[1em]
&=\dfrac{2a+b-a}{2}\\[1em]
&=\dfrac{a+b}{2}\end{align}$
남은 $b<a$에 대한 증명은 스스로 해보길 바란다.
중점의 좌표와 평균
정의에 따르면 중점의 좌표는 두 좌표의 중간값이 되어야 하고 이는 $a,\;b$의 평균을 구하면 중점의 좌표가 됨을 의미한다.
이렇게 사고하는것은 공식을 증명하는 것 보다 훨씬 수월하다고 생각할 수 있지만, 직관으로만 수학을 다루면 정확한 수식과 논리에 약해질 수 밖에 없다. 따라서 수식으로 엄밀하게 보이는 것과 직관적인 이해를 병행하길 바란다.
정리
직선 반직선 선분의 정의와 기호
- 직선 AB
- 서로 다른 두 점 A, B를 지나 양쪽으로 무한히 길게 뻗은 선
- 기호: $\overleftrightarrow{AB}$
- 반직선 AB
- 점 A에서 시작하여 점 B방향으로 무한히 길게 뻗은 직선의 일부
- 기호: $\overrightarrow{AB}$
- 선분 AB
- 두 점 A, B와 그 사이를 연결하는 직선의 일부
- 기호: $\overline{AB}$
직선의 결정조건
- 서로 다른 두 점
- 한 점과 직선의 방향(평행한 직선, 기울기, 벡터)
두 점 $A,\;B$사이의 거리
- $\overline{AB}$의 길이
- 기호 : $\overline{AB}$
선분 AB의 중점 (두 점 $A(a),\;B(b)$의 중점) $M$ 의 정의와 성질
- 선분 AB의 한 가운데 있는 점
- $\dfrac{1}{2}\overline{AB}=\overline{AM}=\overline{BM}$
- 중점($M$)의 좌표 $\dfrac{a+b}{2}$
이상으로 직선 반직선 선분, 직선의 결정조건, 두 점 사이의 거리, 중점에 대한 정리를 마무리 하도록 하겠다.
