직선 반직선 선분 중점 맞꼭지각 문제 정리

직선 반직선 선분 중점 맞꼭지각 문제 정리

by

이번시간에는 기본 도형과 관련된 문제를 풀어보기로 하자. 기본도형과 직선 반직선 선분 개념을 적용하여 해결할 수 있는 문제를 먼저 다루고 중점과 맞꼭지각 문제를 다루었습니다. 문제를 해결하면서 자신감을 키우길 바랍니다.

학습지 다운로드

기본도형 문제

  1. 선과 선이 만나면 교선이 생긴다.
  2. 면과 면이 만나서 생기는 교선은 직선이다.
  3. 서로 다른 두 점을 지나는 직선은 유일하다.
  4. 서로 다른 세 점을 지나는 평면은 유일하다.

[정답]

  1. F
    • 선과 선이 만나면 교점이 생긴다.
  2. F
    • 원뿔을 평면으로 자르면 교선은 곡선이다.
  3. T
  4. F
    • 일직선 상의 서로다른 세 점을 지나는 평면은 무수히 많다.

직선 반직선 선분

직선 반직선 선분 정의 문제

한 직선 위 의 네 점 $A,\;B,\;C,\;D$ 에 대하여 다음 중 옳지 않은 것을 찾고 이유를 서술하여라.

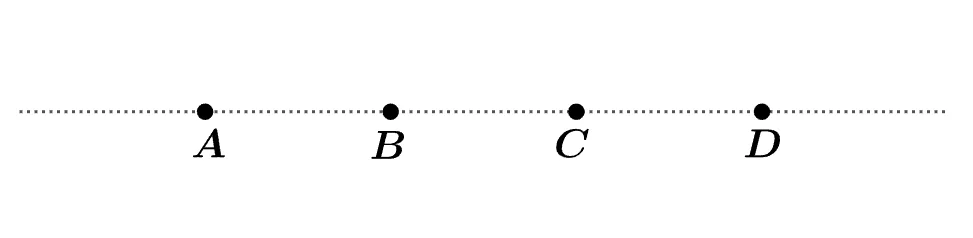
직선 반직선 선분 정의 문제
직선 반직선 선분 정의 문제
  1. $\overleftrightarrow{AB}=\overleftrightarrow{DC}$
  2. $\overrightarrow{AD}=\overrightarrow{DA}$
  3. $\overrightarrow{BC}=\overrightarrow{BD}$
  4. $\overrightarrow{AD}$와 $\overrightarrow{CB}$의 공통 부분은 $\overline{BC}$이다.
  5. $\overline{AC}$와 $\overline{CD}$의 공통부분은 없다.

[정답]

  1. T
  2. F
    • $\overrightarrow{AD}$는 오른쪽 $\overrightarrow{DA}$는 왼쪽으로 무한이 뻗어가는 반직선
  3. T
    • 시작점($B$)이 일치하고 방향이 같음.
  4. F
    • 반직선을 그리면 겹치는 부분은 $\overline{AC}$이다.
  5. F
    • 선분은 양 끝점을 포함하고 있으므로 겹치는 부분은 점$C$이다.

직선과 반직선의 개수 문제

문제1

반원 위의 6개의 점에 대하여 두 점을 이어 만들 수 있는 서로 다른 직선의 개수를 $x$, 반직선의 개수를 $y$라고 할 때 $x+y$값을 구하여라.

직선과 반직선의 개수 문제

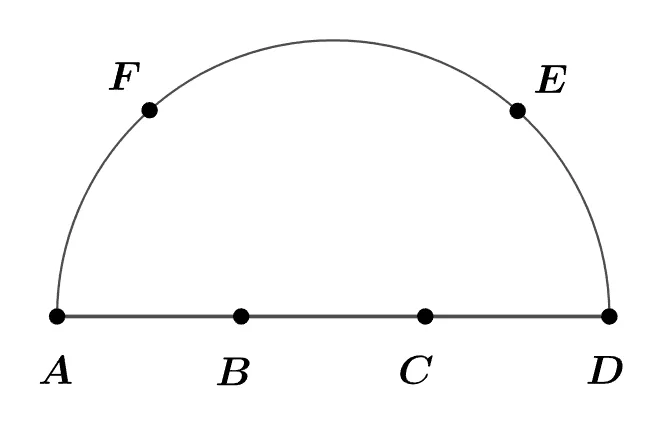
[풀이]

직선의 개수($x$)

네 점을 지나는 직선

A,B,C,D를 지나는 직선: $\bbox[#ffff00]{1}$개

두 점을 지나는 직선

$\begin{cases}
A\text{를 지나는 직선}:\;\overleftrightarrow{AE},\;\overleftrightarrow{AF}\cdots\bbox[#dcff8c]{2} \\[1em]
B\text{를 지나는 직선}:\;\overleftrightarrow{BE},\;\overleftrightarrow{BF}\cdots\bbox[#dcff8c]{2}\\[1em]
C\text{를 지나는 직선}:\;\overleftrightarrow{CE},\;\overleftrightarrow{CF}\cdots\bbox[#dcff8c]{2}\\[1em]
D\text{를 지나는 직선}:\;\overleftrightarrow{DE},\;\overleftrightarrow{DF}\cdots\bbox[#dcff8c]{2}\\[1em]
E\text{를 지나는 직선}:\;\overleftrightarrow{EF}\cdots\bbox[#dcff8c]{1}\\[1em]
\end{cases}$

따라서 $x=\bbox[#ffff00]{1}+\bbox[#dcff8c]{2\times 4+1}=10$이다.

반직선의 개수($y$)

네 점 $A,B,C,D$를 지나는 직선의 일부인 반직선의 개수는 다음과 같이 구할 수 있다.

시작점$\begin{cases} A\;:\overrightarrow{AB}=\overrightarrow{AC}=\overrightarrow{AD}\cdots\bbox[#ffff00]{1}\\[1em]
B\;:\overrightarrow{BA},\;\overrightarrow{BC}=\overrightarrow{BD}\cdots \bbox[#ffff00]{2}\\[1em]
C\;:\overrightarrow{CA}=\overrightarrow{CB},\;\overrightarrow{CD}\cdots\bbox[#ffff00]{2}\\[1em]
D\;:\overrightarrow{DA}=\overrightarrow{DB}=\overrightarrow{DC}\cdots\bbox[#ffff00]{1}\\[1em]
\end{cases}$

  • $\bbox[#ffff00]{1+2+2+1}=6$

두 점을 지나는 직선 $\bbox[#dcff8c]{9}$개에 대한 반직선은 각각 2개씩 존재한다.

  • $\bbox[#dcff8c]{9\times2}=18$

따라서 $y=\bbox[#ffff00]{6}+\bbox[#dcff8c]{18}=24$이다.

$\therefore\; x+y=10+24=34$

문제2

그림과 같이 곡선과 직선으로 둘러 싸인 도형 위의 6개의 점에 대하여 두 점을 이어 만들 수 있는 서로 다른 직선의 개수를 $x$, 반직선의 개수를 $y$라고 할 때 $x+y$값을 구하여라.

직선과 반직선의 개수 문제2

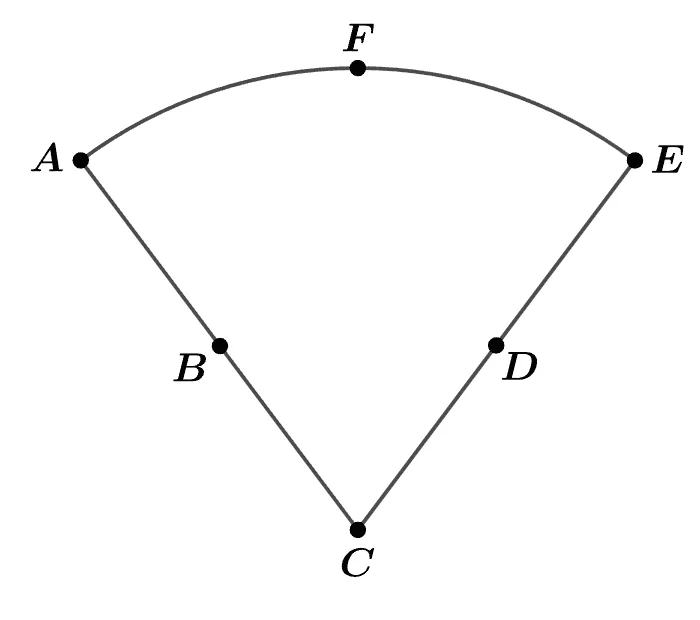
[풀이]요약

직선의 개수($x$)

세 점을 지나는 직선

$\begin{cases} \text{A,B,C를 지나는 직선}\cdots \bbox[#ffff00]{1}\\[1em]
\text{C,D,E를 지나는 직선}\cdots \bbox[#ffff00]{1}\\[1em]
\end{cases}$

두 점만 지나는 직선

$\begin{cases} A\text{와} D, E, F \text{를 지나는 직선} \cdots \bbox[#dcff8c]{3}\\[1em]
B\text{와} D, E, F \text{를 지나는 직선} \cdots \bbox[#dcff8c]{3}\\[1em]
C\text{와} F \text{를 지나는 직선} \cdots \bbox[#dcff8c]{1}\\[1em]
D\text{와} F \text{를 지나는 직선} \cdots \bbox[#dcff8c]{1}\\[1em]
E\text{와} F \text{를 지나는 직선} \cdots \bbox[#dcff8c]{1}\\[1em]
\end{cases}$

  • $x=\bbox[#ffff00]{2}+\bbox[#dcff8c]{9}=11$

반직선의 개수

세 점 A,B,C를 지나는 직선의 일부인 반직선의 개수는 다음과 같이$\bbox[#ffff00]{4}$개이다.

시작점$\begin{cases} A\;:\overrightarrow{AB}=\overrightarrow{AC} \cdots\bbox[#ffff00]{1}\\[1em]
B\;:\overrightarrow{BA},\;\overrightarrow{BC}\cdots \bbox[#ffff00]{2}\\[1em]
C\;:\overrightarrow{CB}=\overrightarrow{CA}\cdots \bbox[#ffff00]{1}\\[1em]
\end{cases}$

세 점 C,D,E를 지나는 직선의 일부인 반직선의 개수도 $\bbox[#ffff00]{4}$개이다.

두 점을 지나는 직선 $\bbox[#dcff8c]{9}$개는 반직선을 2개를 가지고 있다.

따라서 $y=\bbox[#ffff00]{4\times2}+\bbox[#dcff8c]{9\times2}=26$

$\therefore\; x+y=11+26=37$

맞꼭지각 문제(개수)

서로 다른 5개 직선이 한 점에서 만날 때 생기는 맞꼭지각은 몇 쌍인지 구하여라.

맞꼭지각의 개수 문제

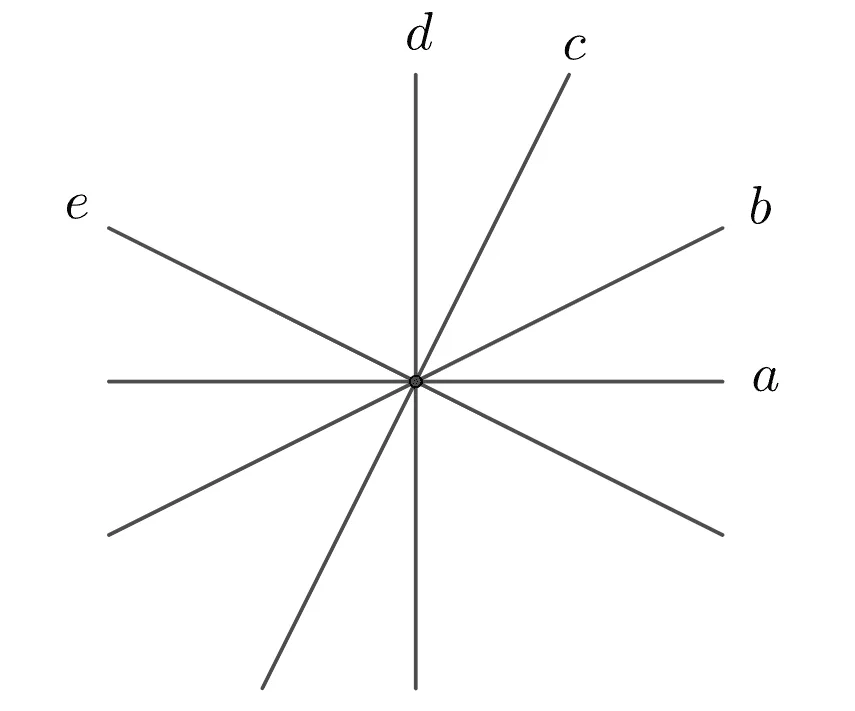
[풀이]

서로 다른 $\bbox[#ffff00]{\text{두 직선}}$이 한 점에서 만날 때 $\bbox[#94feff]{\text{맞꼭지각은 두 쌍}}$ 만들어 진다.

  • $\bbox[#ffff00]{\text{두 직선을 선택할 수 있는 개수}}\times\bbox[#94feff]{2}$

먼저 5개 직선중 2개 직선을 선택하는 방법에 대해 정리해보면 다음과 같다.

(a,b), (a,c), (a,d), (a,e)
(b,c), (b,d), (b,e)
(c,d), (c,e)
(d,e)

$\bbox[#ffff00]{\text{10쌍}}$의 두 직선을 선택할 때마다 서로 다른 $\bbox[#94feff]{\text{두 쌍의 맞꼭지각}}$을 만들 수 있으므로

$\therefore\; \bbox[#ffff00]{10}\times\bbox[#94feff]{2}=20$쌍

중점과 비례 문제

다음 그림에서 세 점 $M, N, P$는 각각 $\overline{AB},\;\overline{MB},\;\overline{AN}$의 중점일 때 $\overline{AB}:\overline{PM}$를 구하여라.

중점과 비례식 문제1

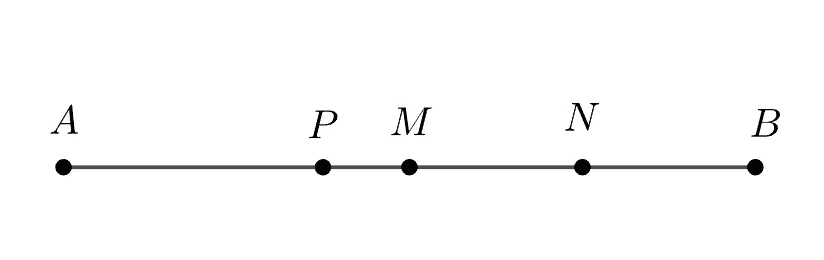
[풀이]

비례식을 편하게 다루기 위해서 짧은 변을 문자로 두는것이 좋다. 여기서는 $\overline{AM}$보다 $\overline{MN}$을 문자로 두는 것이 식을 다루기 편리하다.

  • $\overline{MN}=x$로 두면
    • $\overline{NB}=x,\;\overline{AM}=\overline{MB}=2x$이고
  • $\overline{AN}=3x,\; \bbox[#dcff8c]{\overline{PN}}=\dfrac{3}{2}x$이다.

따라서 $\overline{PM}=\bbox[#dcff8c]{\overline{PN}}-\overline{MN}=\dfrac{1}{2}x$ 이다.

$\therefore\; \overline{AB}:\overline{PM}=4x:\dfrac{1}{2}x=8:1$

맞꼭지각과 비례 문제

문제1

그림에서 다음이 성립할 때 $\angle{COE}$의 크기를 구하여라

  • $5\angle{BOC}=3\angle{BOD}$
  • $3\angle{DOE}=2\angle{EOF}$
맞꼭지각 문제1

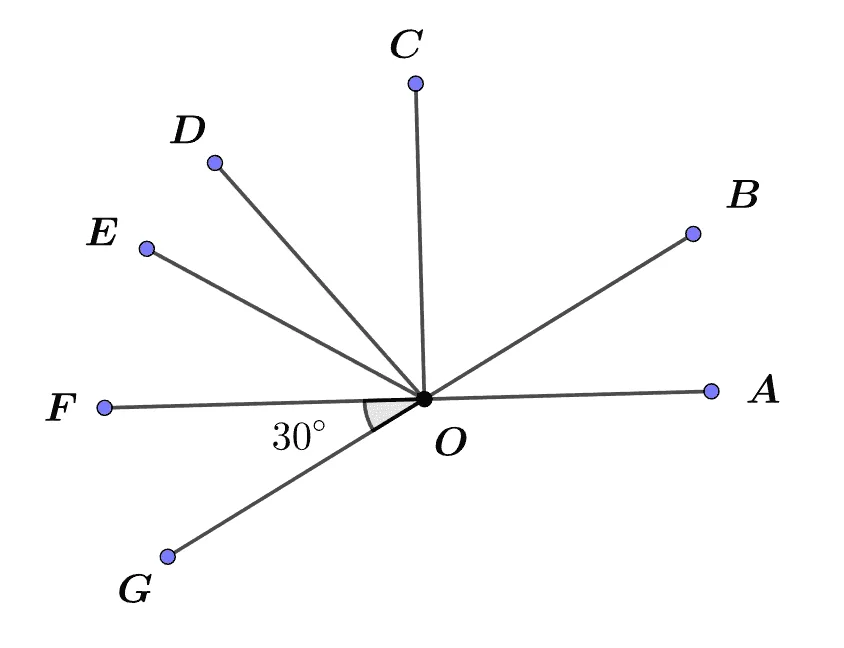
[풀이]

  1. $5\angle{BOC}=3\angle{BOD}$
    • $\angle{BOC}:\angle{BOD}=\dfrac{1}{5}:\dfrac{1}{3}=3:5$
  2. $3\angle{DOE}=2\angle{EOF}$
    • $\angle{DOE}:\angle{COD}=\dfrac{1}{3}:\dfrac{1}{2}=2:3$

자세한 설명은 아래의 비례식 변형식에 대한 설명을 참고하길 바란다.

맞꼭지각과 비례 문제 풀이
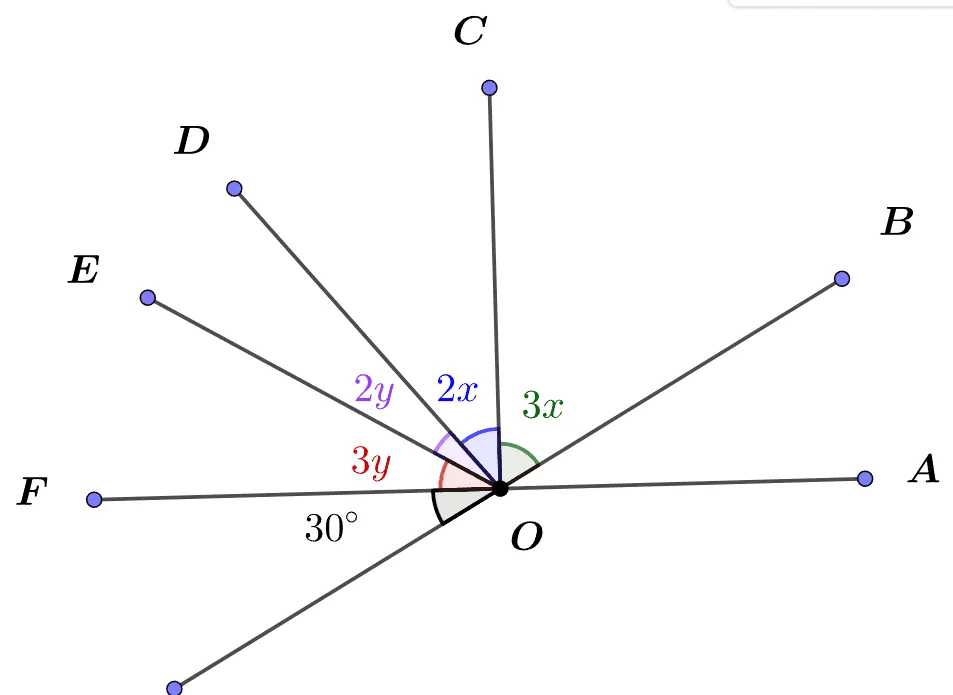
  • $\angle{COE}=2x+2y\;\cdots(1)$
  • $\angle{BOC}+\angle{EOF}=3x+3y\;\cdots(2)$

1.비례배분을 이용한 마무리

$(1)+(2):\;\angle{BOF}=150^\circ$이고 (1), (2)의 비는 2:3이다. 비례배분을 이용하면

$\therefore\; \angle{COE}=150^\circ\times\dfrac{2}{5}=60^\circ$

2.식변형을 이용한 마무리

$\angle{BOF}=5x+5y=5(x+y)=150^\circ$
$\rightarrow x+y=30^\circ$

$\therefore \; \angle{COE}=2x+2y=2(x+y)=60^\circ$

문제2

그림과 같이 한 점에서 만나는 $\overline{AB},\;\overline{CD},\;\overline{EF}$와 $\angle{a},\; \angle{b},\;\angle{c}$에 대하여 다음이 성립할 때 $\angle{AOD}$의 크기를 구하여라.

  • $6\angle{a}=3\angle{b}=2\angle{c}$
각과 비례 문제2

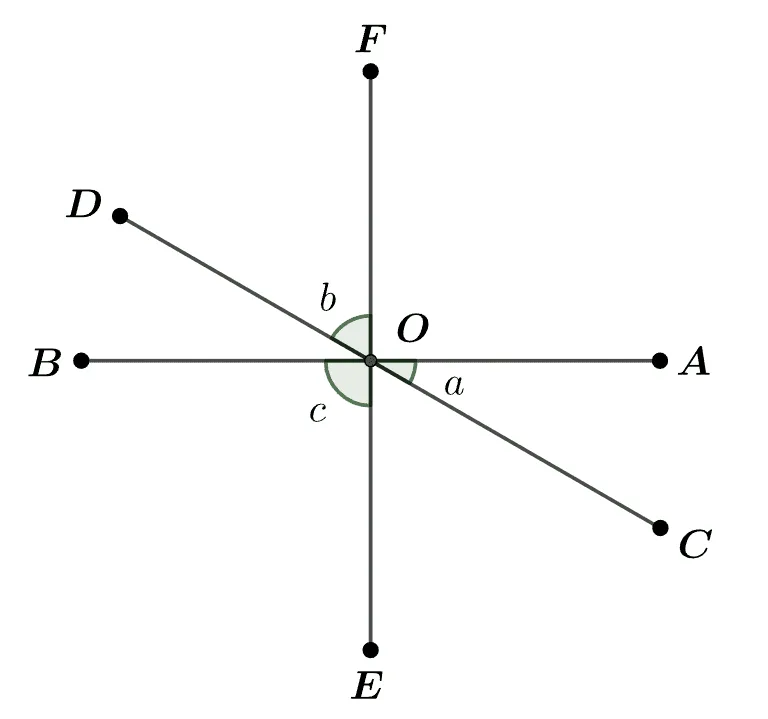
[풀이]

$6\angle{a}=3\angle{b}=2\angle{c}=x$에 대하여

$\angle{a}:\angle{b}:\angle{c}=\dfrac{1}{6}:\dfrac{1}{3}:\dfrac{1}{2}=1:2:3$

$a+b+c=180^\circ,\; a:b:c=1:2:3$이고 비례배분을 이용하면

  • $a=180^\circ\times \dfrac{1}{1+2+3}=30^\circ\\[1em]$
  • $b=180^\circ\times \dfrac{2}{1+2+3}=60^\circ\\[1em]$
  • $c=180^\circ\times \dfrac{3}{1+2+3}=90^\circ\\[1em]$

$\therefore\;\angle{AOD}=b+c=150^\circ$

보충이론 비례식

비례배분 (초등)

  • 비례배분 : 전체의 양을 주어진 비로 배분하는 것

예시) 사탕 40개를 두 명에게 3:5로 배분하여라.

  • 나누어 주는 량 : $3x, 5x$
  • 나누기 전 전체량 : $\bbox[#ffff00]{8x}$
  • 배분 비율 : $\dfrac{3x}{\bbox[#ffff00]{8x}}=\dfrac{3}{\bbox[#ffff00]{8}},\;\dfrac{5x}{\bbox[#ffff00]{8x}}=\dfrac{5}{\bbox[#ffff00]{8}}$
  • 배분 개수 : $\text{사탕개수}\times\text{배분 비율}$
    • $40\times\dfrac{3}{\bbox[#ffff00]{8}}=15$
    • $40\times\dfrac{5}{\bbox[#ffff00]{8}}=25$

예시) 사탕 48개를 세 명에게 2:3:7로 배분하여라.

2:3:7의 비로 배분할 때 전체량은 $2+3+7=12$의 비를 갖고 비율을 이용해 다음과 같이 계산할 수 있다.

  • $48\times\dfrac{2}{\bbox[#dcff8c]{12}}=8$
  • $48\times\dfrac{3}{\bbox[#dcff8c]{12}}=12$
  • $48\times\dfrac{7}{\bbox[#dcff8c]{12}}=28$

비례식의 변형식

[1] $2a=3b$일 때 a:b는 2,3의 역수의 비와 같다.

[설명]

$2a=3b=x$로 두면 $a:b=\dfrac{x}{2}:\dfrac{x}{3}=\dfrac{1}{2}:\dfrac{1}{3}$이다.

[2] $2a=3b=6c$일 때 a:b:c는 2,3,6의 역수의 비와 같다.

[설명]

$2a=3b=6c=x$로 두면 $a:b:c=\dfrac{x}{2}:\dfrac{x}{3}:\dfrac{x}{6}=\dfrac{1}{2}:\dfrac{1}{3}:\dfrac{1}{6}$이다.

맺음말

문제를 통해 직선 반직선 선분 맞꼭지각 중점에 대한 개념을 더 정확히 이해할 수 있었길 바랍니다.

중학교 1학년 목차

전체 목차 (홈페이지)