삼각형의 닮음은 도형의 크기는 다르지만 모양이 같은 관계를 의미합니다. 수학에서 닮음 개념은 비례식, 합동, 그리고 삼각비와도 깊은 관련이 있으며, 중학교 도형 단원에서 매우 중요한 핵심 개념 중 하나입니다. 이 글에서는 삼각형의 닮음 조건(SSS, SAS, AA)과 직각삼각형 닮음 공식 응용까지 단계별로 정리해 보았습니다.
삼각형의 닮음 조건
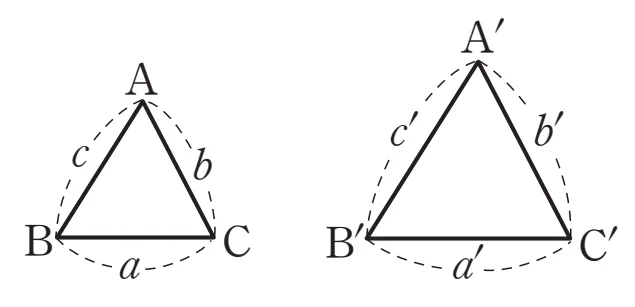
두 삼각형이 다음 세 조건 중 어느 하나를 만족시키면 서로 닮음이 됩니다.
조건1. SSS 닮음
세 쌍의 대응변의 길이의 비가 같다.
$a:a’=b:b’=c:c’$
조건2. SAS 닮음
두 쌍의 대응변의 길이의 비가 같고, 그 끼인각의 크기가 같다.
$a:a’=c:c’$이고 $\angle B=\angle B’$
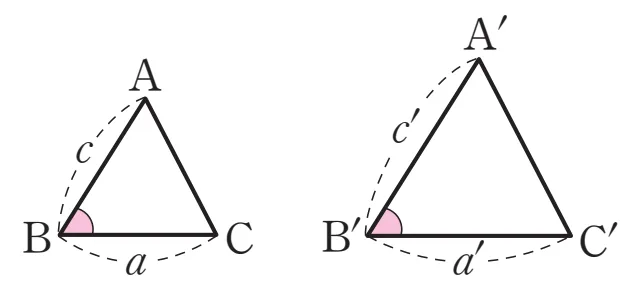
조건3. AA 닮음
두 쌍의 대응각의 크기가 각각 같다.
$\angle B=\angle B’,\ \angle C=\angle C’$
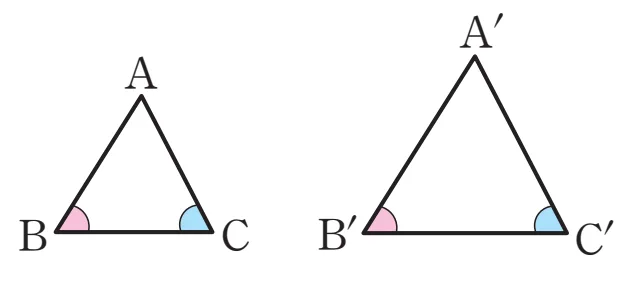
닮음 조건에서 닮음비가 $1:1$ $\Rightarrow$ 합동조건
- SSS 닮음 $\Rightarrow$ 세 쌍의 대응변의 길이가 각각 같다. (SSS 합동)
- SAS 닮음 $\Rightarrow$ 두 쌍의 대응변의 길이가 각각 같고, 그 끼인각의 크기가 같다. (SAS 합동)
- AA 닮음 $\Rightarrow$ 한 쌍의 대응변의 길이가 같고, 그 양 끝 각의 크기가 각각 같다. (ASA 합동)
닮음 조건 적용 예제
간단한 예시를 통해 닮음 조건을 적용하는 방법에 대해 살펴봅시다.
예제1.
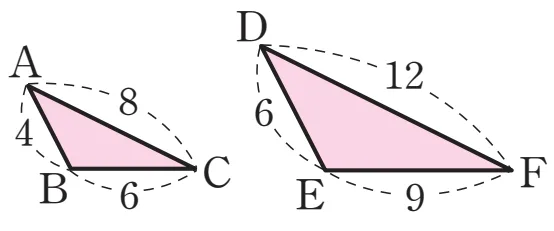
닮음 설명
$\overline{AB}:\overline{DE}=4:6=2:3$
$\overline{BC}:\overline{EF}=6:9=2:3$
$\overline{AC}:\overline{DF}=8:12=2:3$
따라서 세 쌍의 대응변의 길이의 비가 같으므로 $\triangle ABC \sm \triangle DEF$ (SSS 닮음)
예제2.
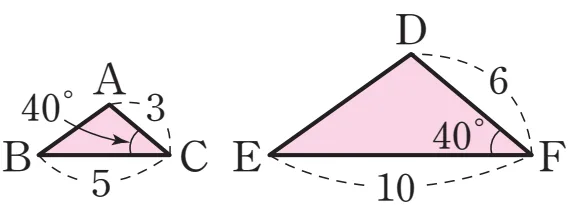
닮음 설명
$\overline{BC}:\overline{EF}=5:10=1:2$
$\overline{AC}:\overline{DF}=3:6=1:2$
$\angle C=\angle F=40^\circ$
두 쌍의 대응변의 길이의 비가 같고 끼인각의 크기가 같으므로 $\triangle ABC \sm \triangle DEF$ (SAS 닮음)
예제3.
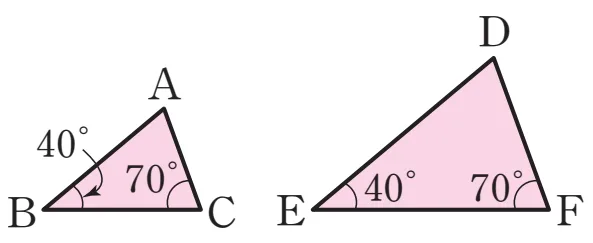
닮음 설명
$\angle B=\angle E=40^\circ$
$\angle C=\angle F=70^\circ$
두 쌍의 대응각의 크기가 각각 같으므로 $\triangle ABC \sm \triangle DEF$ (AA 닮음)
삼각형의 닮음 응용
SAS 닮음의 응용
공통인 각을 끼인각으로 하는 두 쌍의 대응변의 길이의 비가 같은 두 삼각형을 찾는 유형으로 예를 들면 아래와 같습니다.
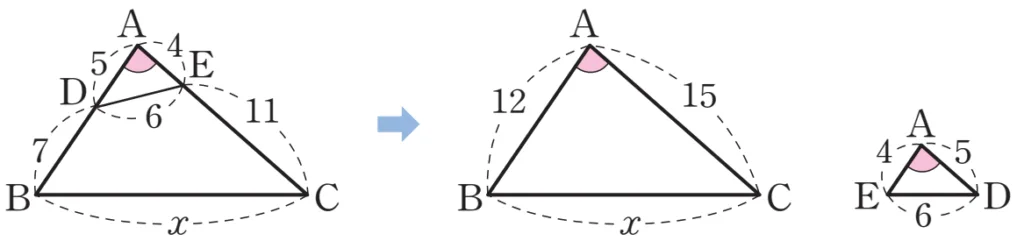
풀이
$\triangle ABC$와 $\triangle AED$에서
$\angle A$는 공통, $\overline{AD}:\overline{AC}=\overline{AE}:\overline{AB}=3:1$ 이므로
$\triangle ABC \sm \triangle AED$ (SAS 닮음)
따라서 $\overline{DE}:\overline{BC}=6:x=1:3\ \Rightarrow\ x=18$
AA 닮음의 응용
두 삼각형의 한 각이 공통일 떄 AA 닮음은 크게는 두 유형으로 나눌 수 있습니다.
- 나머지 대응점이 동일한 위치에 있는 경우 (유형1)
- 나머지 대응점이 반대 위치에 있는 경우 (유형2, 3)
각 유형에서 닮음비와 세 변사이의 비례식이 성립합니다.

- 유형1
- 닮음비 $\bbox[#ffff00]{\text{작은삼각형}} : \bbox[#dcff8d]{\text{큰삼각형}}$
$\bbox[#ffff00]{\overline{AD}}:\bbox[#dcff8d]{\overline{AB}}=\bbox[#ffff00]{\overline{AE}}:\bbox[#dcff8d]{\overline{AC}}=\bbox[#ffff00]{\overline{DE}}:\bbox[#dcff8d]{\overline{BC}}$ - $\triangle ADE ,\ \triangle ABC$ 세 변 사이의 비
$\bbox[#ffff00]{\overline{AD}:\overline{AE}:\overline{DE}}=\bbox[#dcff8d]{\overline{AB}:\overline{AC}:\overline{BC}}$
- 닮음비 $\bbox[#ffff00]{\text{작은삼각형}} : \bbox[#dcff8d]{\text{큰삼각형}}$
- 유형2
- 닮음비 $\bbox[#ffff00]{\text{작은삼각형}} : \bbox[#dcff8d]{\text{큰삼각형}}$
$\bbox[#ffff00]{\overline{AD}}:\bbox[#dcff8d]{\overline{AC}}=\bbox[#ffff00]{\overline{AE}}:\bbox[#dcff8d]{\overline{AB}}=\bbox[#ffff00]{\overline{DE}}:\bbox[#dcff8d]{\overline{BC}}$ - $\triangle ADE ,\ \triangle ABC$ 세 변 사이의 비
$\bbox[#ffff00]{\overline{AD}:\overline{AE}:\overline{DE}}=\bbox[#dcff8d]{\overline{AC}:\overline{AB}:\overline{BC}}$
- 닮음비 $\bbox[#ffff00]{\text{작은삼각형}} : \bbox[#dcff8d]{\text{큰삼각형}}$
- 유형3
- 닮음비 $\bbox[#ffff00]{\text{작은삼각형}} : \bbox[#dcff8d]{\text{큰삼각형}}$
$\bbox[#ffff00]{\overline{AB}}:\bbox[#dcff8d]{\overline{AC}}=\bbox[#ffff00]{\overline{AE}}:\bbox[#dcff8d]{\overline{AB}}=\bbox[#ffff00]{\overline{BE}}:\bbox[#dcff8d]{\overline{BC}}$ - $\triangle ADE ,\ \triangle ABC$ 세 변 사이의 비
$\bbox[#ffff00]{\overline{AB}:\overline{AE}:\overline{BE}}=\bbox[#dcff8d]{\overline{AC}:\overline{AB}:\overline{BC}}$
- 닮음비 $\bbox[#ffff00]{\text{작은삼각형}} : \bbox[#dcff8d]{\text{큰삼각형}}$
유형1과 같이 대응점이 나란히 있으면 닮음비를 생각하기 쉽습니다. 하지만 대응점이 반대에 있는 경우 닮음비를 생각할 때 반대쪽에서 대응변을 찾아 비례식을 만들어야 합니다.
닮음인 경우 닮음비 이외에도 세 변 사이의 비율이 같기 때문에 세 변 사이의 비례식을 이용 할 수 도 있습니다.
유형3에 대한 예제를 살펴보고 다음으로 넘어가도록 하겠습니다.
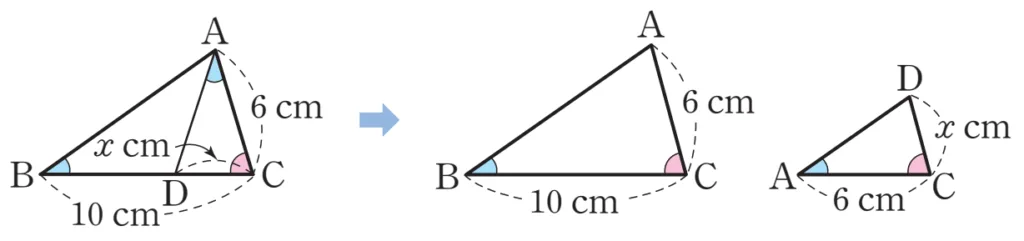
풀이
$\triangle ABC$와 $\triangle DAC$에서 $\angle C$는 공통, $\angle ABC=\angle DAC$ 이므로
$\triangle DAC \sm \triangle ABC$ (AA 닮음)
$\triangle{DAC}$에서 $\overline{CA}:\overline{CD}$를 이용할 때
$\triangle{ABC}$에서는 이 두 변의 위치와 반대되는 순서로
$\overline{CB}:\overline{CA}$를 비례식으로 세우면 됩니다.
따라서 $\overline{CA}:\overline{CD}=\overline{CB}:\overline{CA}$ 이므로 $6:x=10:6\ \Rightarrow\ x=\dfrac{36}{10}=\dfrac{18}{5}$
직각삼각형 닮음 공식
$\angle A=90^\circ$인 직각삼각형 $ABC$에서 꼭짓점 $A$에서 빗변 $BC$에 내린 수선의 발을 $H$라 할 때, 다음이 성립합니다.
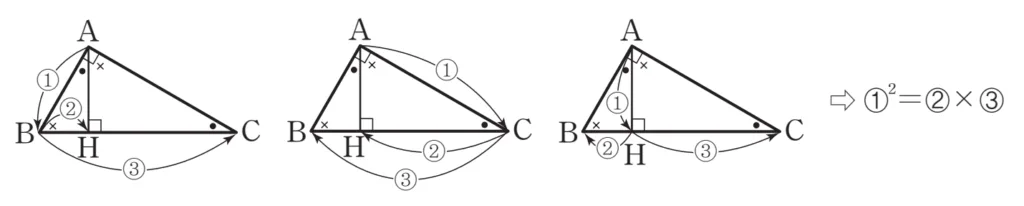
직각삼각형 닮음 공식으로 알려진 위의 사실은 아래와 같이 증명할 수 있습니다.
닮음 관계식1
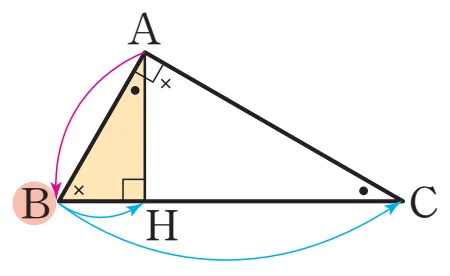
설명
$\triangle ABC \sm \triangle HBA$ (AA 닮음)
$\overline{AB}:\overline{BC}=\overline{BH}:\overline{AB}\ \Rightarrow\ \overline{AB}^{2}=\overline{BH}\cdot\overline{BC}$
닮음 관계식2
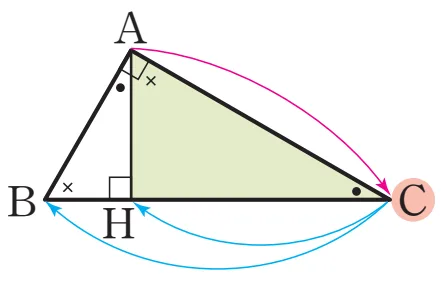
설명
$\triangle ABC \sm \triangle HAC$ (AA 닮음)
$\overline{AC}:\overline{BC}=\overline{HC}:\overline{AC}\ \Rightarrow\ \overline{AC}^{2}=\overline{CH}\cdot\overline{CB}$
닮음 관계식3
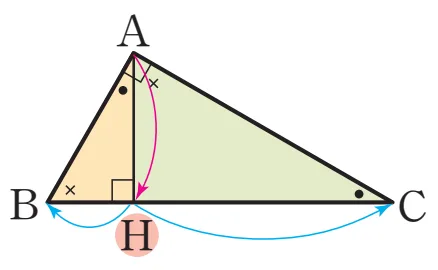
설명
$\triangle HBA \sm \triangle HAC$ (AA 닮음)
$\overline{HA}:\overline{HC}=\overline{HB}:\overline{HA}\ \Rightarrow\ \overline{HA}^{2}=\overline{HB}\cdot\overline{HC}$
넓이 관계식
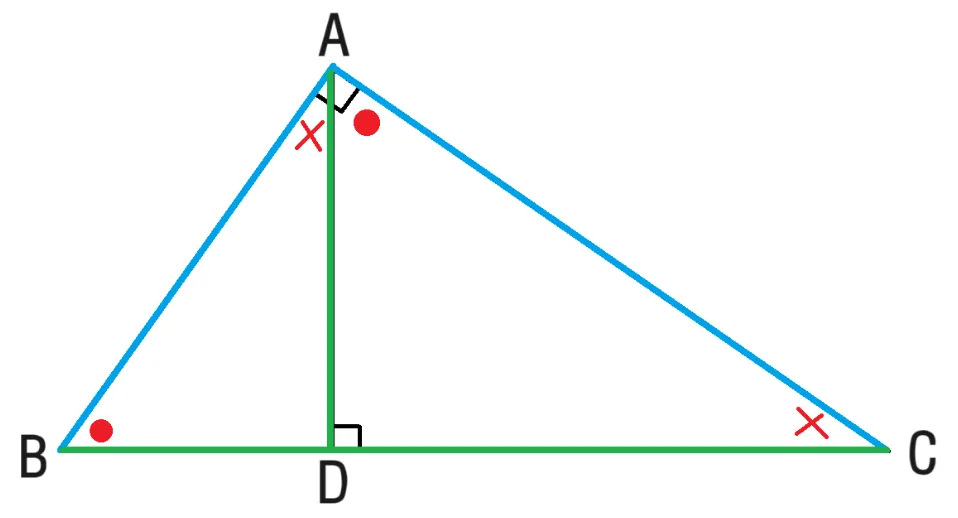
설명
$\triangle{ABC}$의 넓이에 대하여,
$\dfrac{1}{2}\overline{BC}\times \overline{AD}=\dfrac{1}{2}\overline{AB}\times\overline{AC}$ 이므로
$\overline{BC} \times\overline{AD}=\overline{AB}\times\overline{AC}$ 가 성립한다.
[출처: 개념원리]
