줄기와 잎 그림 특징 제한점

이번 시간에는 수량으로 주어진 자료(변량)를 정리하는 방법으로 줄기와 잎 그림에 대해 정리해 보려고 합니다.

줄기와 잎 그림

• 줄기와 잎 그림 : 줄기와 잎을 이용해 자료(변량)를 나타낸 것
• 표기 : $\bbox[#ffff00]{\text{줄기}} | \bbox[#dcff8c]{\text{잎}}$
  $12\;\rightarrow\;\bbox[#ffff00]{1}|\bbox[#dcff8c]{2}$
  $126\;\rightarrow\;\bbox[#ffff00]{12}|\bbox[#dcff8c]{6}$
  • 줄기 : 왼쪽 표기, 일의 자리를 제외한 수
  • 잎 : 오른쪽 표기, 일의 자리 수

그리는 방법 (순서)

줄기와 잎 그림을 그리는 방법은 다음과 같다.

1. 변량을 보고 $\bbox[#ffff00]{\text{줄기}} | \bbox[#dcff8c]{\text{잎}}$을 설명
2. 세로 선을 긋는다.
   • 왼쪽 : 줄기, 작은 값 부터 세로로 적는다.
     • 한 자리수 : $3 \rightarrow \; \bbox[#ffff00]{0}|\bbox[#dcff8c]{3}$
   • 오른쪽 : 잎, 작은 값부터 가로로 적는다.
     • 중복 변량 : 중복 횟수 만큼 적는다.
     • 세로 줄 맞춰서 적는다.

예시

A반과 B반의 수학 단원 평가 성적을 줄기와 잎 그림으로 정리해 보자.

[A 반 단원평가 점수]

[A반 단원평가 점수] ($\bbox[#ffff00]{1} | \bbox[#dcff8c]{2}=12$)

[B 반 성적]

[B반 단원평가 점수] ($\bbox[#ffff00]{1} | \bbox[#dcff8c]{2}=12$)

줄기와 잎 그림 : 두 집단 비교

두 집단을 비교할 때 줄기와 잎 그림을 다음과 같이 응용할 수 있다.

[A, B반 단원평가 점수]

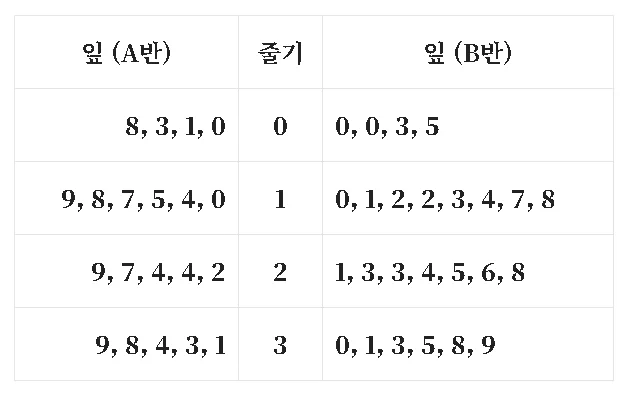
특징과 제한점

특징

• 자료의 분포를 한 눈에 파악
• 원자료의 값을 유지
• 자료를 크기순 으로 나열
  • 특정 위치의 값 찾기 편리

제한 사항

• 변량의 수가 많으면 정리 어려움
• 변량이 밀집되어 있을 때
• 변량이 넓게 분산되어 있을 때

이러한 제한 사항은 도수분포표를 이용하면 해결할 수 있다.

• 도수분포표 포스팅

중고등학교 통계 프로그램 사이트

중고등학교 통계수업에 활용할 수 있는 프로그램을 제공하는 사이트 입니다.

• 통계교육원(통그라미)