이번시간에는 좌표와 좌표평면에 대한 기본적인 용어와 개념을 정리해 보도록 하자.
목차
좌표와 좌표평면
좌표는 한 점에 대응하는 수를 의미하고 일반적으로 ‘점 $P$에 대응하는 좌표’ 로 사용한다. 간단히 좌표의 정의를 정리하고 수직선과 좌표평면위의 점에서 좌표를 표기하는 방법에 대해 알아보기로 하자.
- 점$P$의 좌표 : 점 $P$에 대응하는 수 또는 순서쌍
수직선 위의 점P의 좌표
주어진 직선에서 한 점의 위치를 표현하기 위해 ‘0’을 기준으로 수직선을 그려 점의 위치를 수로 나타낸다. 다음의 예를 통해 살펴보자.
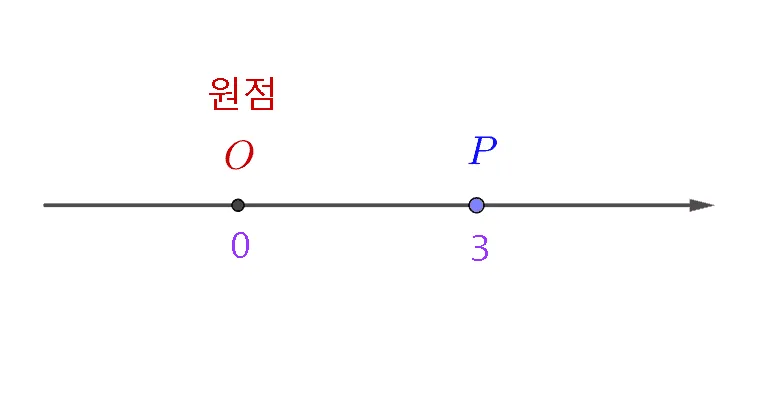
점은 일반적으로 대문자로 나타내고, 대문자 $O$의 경우는 $0$에서만 사용한다. 용어와 표기법을 정리하면 다음과 같다.
- 점$P$의 좌표는 3이다 $\xrightarrow[]{\text{표기}}\; P(3)$
- 점 $O$ : 원점 $\xrightarrow[]{\text{표기}}\; O(0)$
좌표평면 위의 점P의 좌표
평면상의 한 점의 위치를 표현하려면 좌, 우 방향의 수직선과 상, 하 방향의 수직선이 필요하다. 이 두 수직선을 원점에서 수직으로 겹치면 다음과 같고 이를 좌표평면이라고 한다. 먼저 좌표평면의 용어를 정리하고 평면상의 점 $P$를 표기하는 방법에 대하여 정리해 보자.
좌표평면 용어정리
다음을 통해 좌표평면의 기본적인 용어를 정리해 보도록 하자.
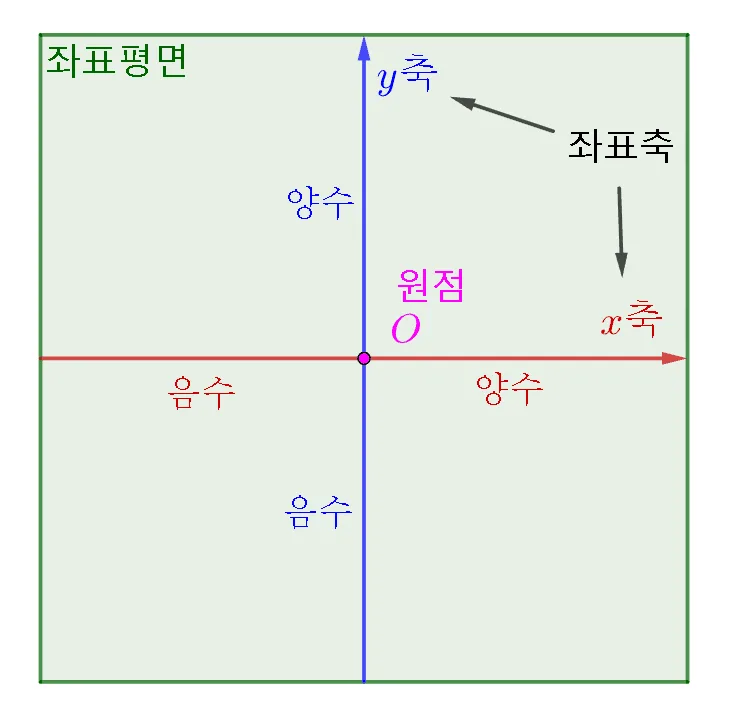
- $\text{좌표축} \begin{cases} x \; \text{축: 가로 수직선}\\ y\; \text{축: 세로 수직선} \end{cases}$
- 원점 $O$ : 좌표축의 교점
- 좌표평면 : 좌표축이 정해져서 점의 위치를 나타낼 수 있는 평면
평면에서 점의 좌표
평면에서 점의 위치를 나타내는 방법에 대해 다음의 그림을 보며 정리해 보자.
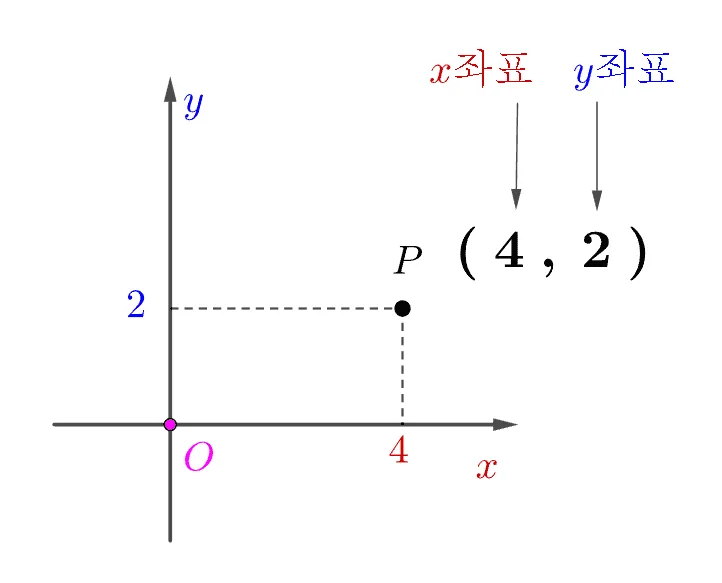
평면은 두 개의 수직선으로 위치를 표현할 수 있고, 점의 좌표는 각 수직선에 대응되는 값을 이용해 표현 할 수 있다. 이 때 두 수직선의 좌표를 각 각 $x$좌표 $y$좌표라 하고 둘의 순서를 약속하여 점의 좌표를 다음과 같이 나타낸다.
- 순서쌍 : 순서를 생각하여 수를 짝지은 것 $(a,\;b)$
- 점 $P$의 좌표 : $(4,2)$ $\xrightarrow[]{\text{표기}}\; P\;(4,\;2)\\[1em]$
- $P\;(a,\;b)\;\begin{cases} a\;:\; \text{점 P의 x좌표}\\[1em]b\;:\; \text{점 P의 y좌표}\end{cases}$
좌표축 위의 점
좌표축 위에 있는 점의 좌표에 대해 다음을 보며 정리해 보자.
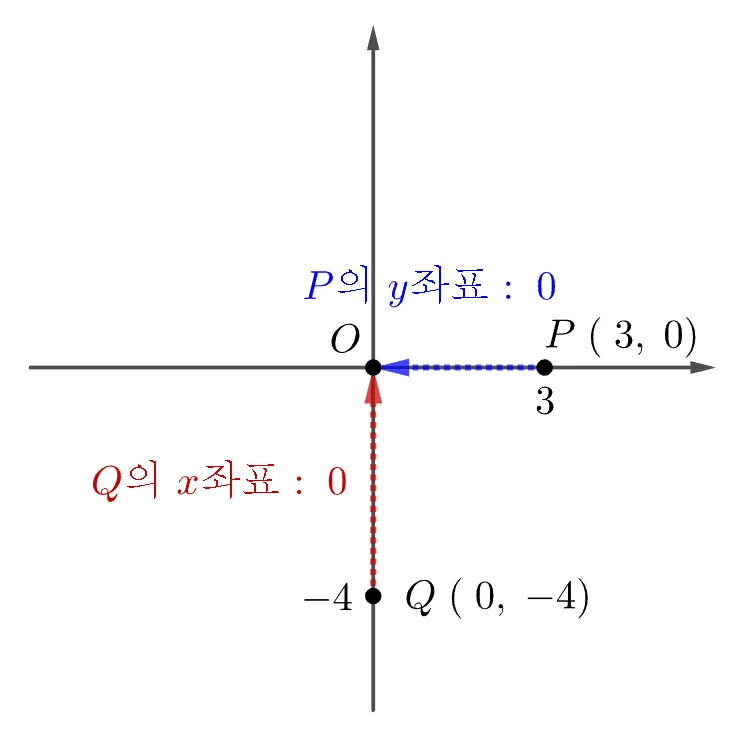
그림을 통해 살펴보면 좌표축 위의 점의 좌표를 정리하면 다음과 같다.
- $x$축 위의 점 : $y$좌표값이 0 이다.
- $y$축 위의 점 : $x$좌표값이 0 이다.
이를 문자로 다음과 같이 간단히 표현 할 수 있다.
$\text{좌표축 위의 점}\begin{cases} x\text{축 위의 점}:\; (a,0)\\[1em]
y\text{축 위의 점}:\; (0,b)\end{cases}$
사분면
좌표평면은 두 좌표축에 의해 데 부분으로 나누어 지는데 이를 사분면이라고 한다. 각 사분면의 이름과 사분면 위의 점의 좌표에서 부호는 아래와 같이 결정된다.
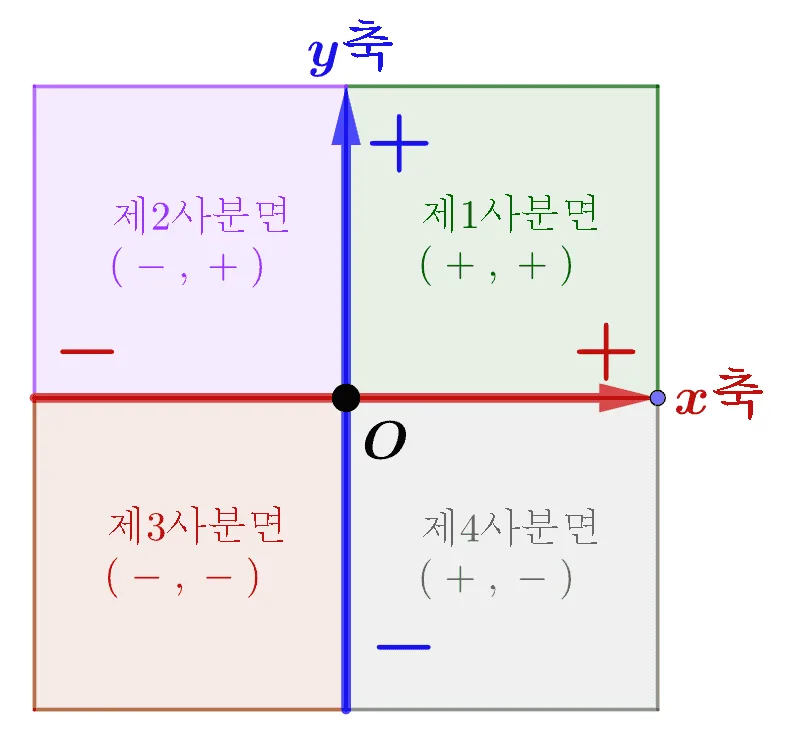
주의할 사항은 원점과 좌표축($x$축, $y$축)은 어느 사분면에도 포함되지 않는다는 사실이다. 이를 정리하면 다음과 같다.
$\text{좌표평면}\begin{cases}
\text{좌표축}\begin{Bmatrix} x\;\text{축}\\[1em] y\;\text{축}\end{Bmatrix}\xrightarrow[]{\text{교점}}\text{원점}\;O\\[1em]
\text{사분면: 제1,2,3,4 사분면}\end{cases}$
점의 이동
수학에서 점을 이동시키는 대표적인 방법은 대칭이동과 평행이동이다. 좌표평면위의 점을 이동하는 방법에 대해 정리해 보기로 하자.
점의 대칭이동
먼저 축과 원점에 대한 대칭이동을 다음 그림을 통해 정리해 보자.
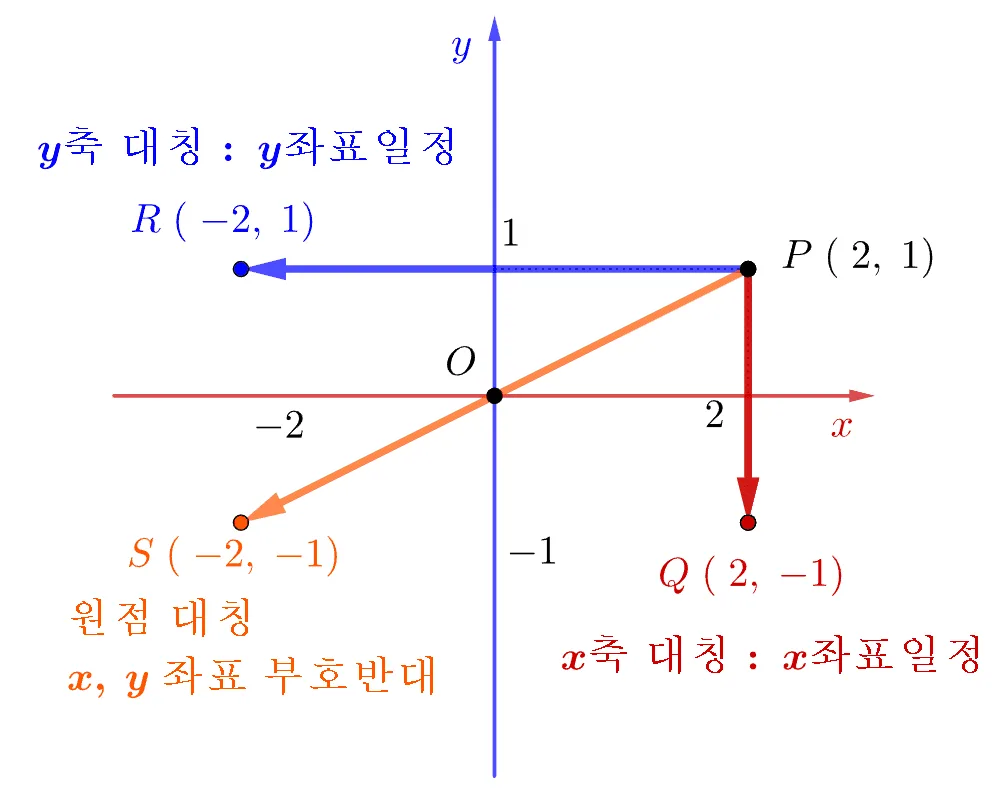
$P \rightarrow Q$에 대해 생각해 보면 $x$축 대칭이동에서 $x$좌표는 그대로 유지되고 $y$좌표의 부호는 반대로 바뀐다. 비슷한 과정에 의해 $P \rightarrow R$ 를 통해 $y$축 대칭이동은 $y$좌표가 그대로 유지되고 $x$좌표의 부호가 반대임을 알 수 있다. 반면에 원점에 대한 대칭은 $x$좌표 $y$좌표의 부호가 모두 반대임을 알 수있다. 이를 문자를 이용해 정리하면 다음과 같다.
$P(a,b) \text{대칭이동} \begin{cases} \text{좌표축}\begin{cases} x\text{축 대칭: }(a,-b)\\[1em] y\text{축 대칭: }(-a,b)\end{cases}\\[1em]
\text{원점 대칭: }(-a,-b)\end{cases}$
점의 평행이동
점의 평행이동에 대하여 다음의 그림을 이용해 정리해 보자.
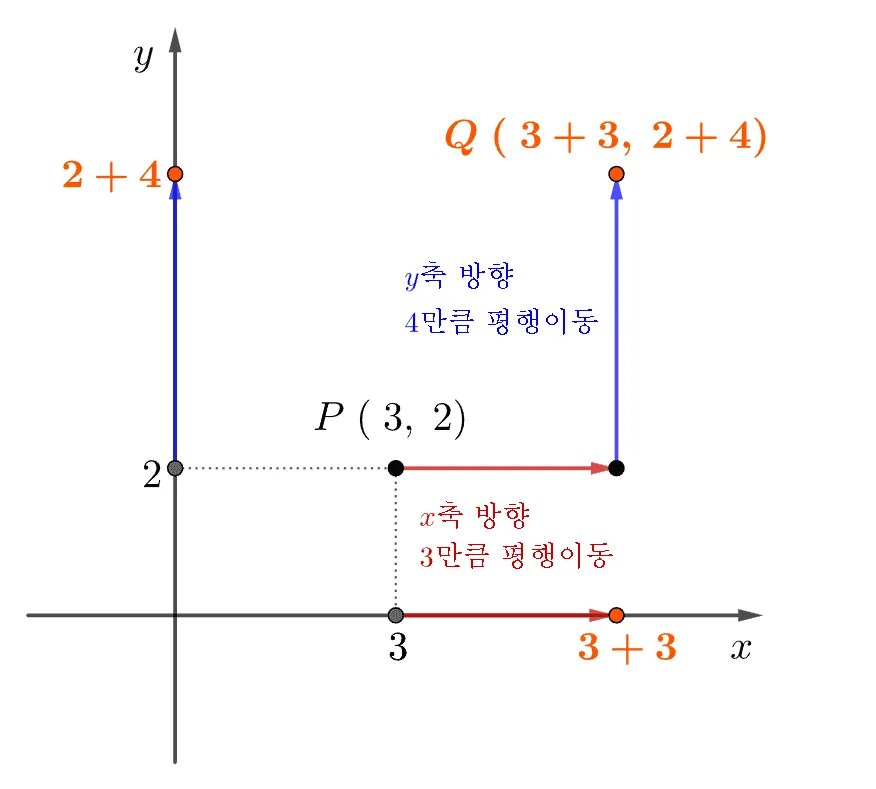
점$P(3,2)$를 $x$축 방향으로 $\bbox[#ffff00]{3}$만큼 $y$축 방향으로 $\bbox[#dcff8c]{4}$만큼 평행이동 한 점Q의 좌표는 위와 같은 이유로 $Q(3+\bbox[#ffff00]{3},\;2+\bbox[#dcff8c]{4})$이다. 위의 사실을 문자를 이용해 정리해 보면 다음과 같다.
점 $P(a,b)$를 $x$축으로 $\bbox[#ffff00]{p}$만큼, $y$축으로 $\bbox[#dcff8c]{q}$만큼 평행이동한 점 $Q$의 좌표는 다음과 같다.
- $Q(a+\bbox[#ffff00]{p},\;b+\bbox[#dcff8c]{q})$
이상으로 좌표와 좌표평면에 대한 기본적인 개념에 대한 정리를 마무리 하도록 하겠다.
