정다면체 5개인 이유 증명, 꼭짓점 모서리 개수 표 정리

이번 시간에는 정다면체의 정의를 토대로 정다면체의 개수가 5개인 이유에 대해 증명하고, 꼭짓점 모서리 개수를 구하는 방법에 대해 학습하고, 학습한 내용을 표를 이용해 정리해 봅시다.

정다면체

다면체: 다각형 ($n$각형)으로만 둘러싸인 입체도형

• 정다면체: 아래 두 조건을 만족하는 $\colorbox{#ffff00}{다면체}$
  • 모든 면이 $\colorbox{#dcff8c}{합동}$인 $\colorbox{#dcff8c}{정다각형}$
  • $\colorbox{#94feff}{한 꼭짓점}$에 모인 $\colorbox{#94feff}{면의 개수}$ 일정
• 이름: 면의 개수에 따라 $\rightarrow$ 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체 (정다면체는 5개 뿐이다!)

보충설명

정의 적용

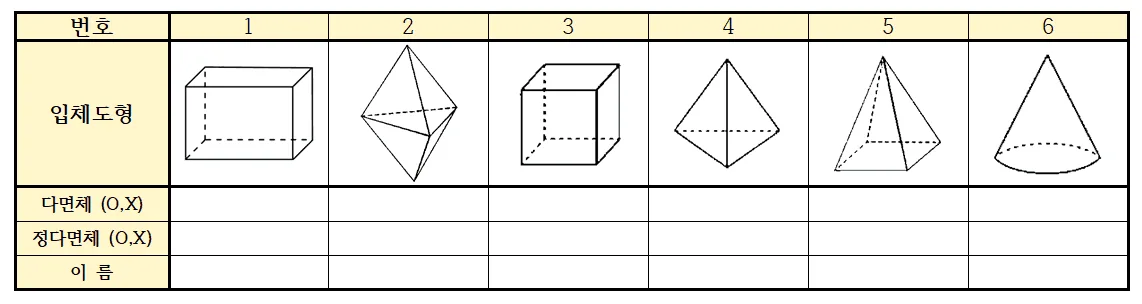
다면체에 대한 내용은 전시간에 정리 하였으므로 간단히 언급만 하고, 이번시간에는 정다면체를 집중적으로 다루도록 하겠다.

• 다면체를 모두 고르면? 1,2,3,4,5

[적용1] 2번, 5번 다면체가 정다면체인지 아닌지 이유를 들어 설명하여라.

• 2번 : 정다면체가 아니다.
  • 모든 면이 합동인 정삼각형이지만, 한 꼭짓점에 모인 면의 개수가 3개인 것과 4개인 것이 있다.
• 3번 : 정다면체가 아니다.
  • 정삼각형, 정사각형이 같이 있어 합동이 아니고, 한 꼭짓점에 모인 면의 개수도 다르다.

[적용2] 다면체의 이름을 적어라.

• 1: 육면체, 직육면체
• 2: 육면체
• 3: 육면체, 정육면체
• 4: 사면체, 정사면체
• 5: 오면체, 사각뿔
• 6: 원뿔 (회전체) 다음 학습 내용

정다면체 5개 뿐인 이유 증명

정다면체의 정의에 따라 두 가지 조건에 맞는 다면체를 체계적으로 정리해 보자.

• 조건1: 모든 면이 $\colorbox{#dcff8c}{합동}$인 $\colorbox{#dcff8c}{정다각형}$
• 조건2: $\colorbox{#94feff}{한 꼭짓점}$에 모인 $\colorbox{#94feff}{면의 개수}$ 일정

한 꼭짓점에 모인 면의 개수

위의 자료를 토대로 생각하면 입체도형을 만들기 위해 한 꼭짓점에 $\colorbox{#94feff}{최소 3개}$의 면이 모여야 함을 알 수 있다.

합동인 정다각형

정다각형에는 정삼각형, 정사각형, 정오각형 $\cdots$이 있고, 정삼각형 부터 차례로 $\colorbox{#94feff}{3개 이상}$ 모이는 경우를 생각해 보아야 한다. 전체 입체를 생각하기 전에 한 꼭짓점만 전개도로 펼쳐서 생각을 정리해 보자.

정삼각형

• 정삼각형의 한 내각의 크기 : $60^\circ$
• 한 꼭짓점에 모일 수 있는 정사각형 개수 : 3, 4, 5, 6개
  • 3, 4, 5개 $\rightarrow$ 정다면체 가능성 있음
  • 6개 $\rightarrow$ 다면체 구성 불가
    $\because\;60^\circ\times 6 = 360^\circ$
  • 7개 이상
    한 꼭짓점에 모인 각 $ >360^\circ$
    울퉁불퉁한 다면체가 만들어진다.

1의 가능성이 존재성을 보장하지 않기 때문에 직접 확인해 보아야 한다.

직접 만들어 보는것이 가장 좋은 방법이지만 여기서는 간단한 영상으로 존재함을 보이고 넘어가도록 하겠습니다.

따라서 한 꼭짓점에 정삼각형이 3, 4, 5개 모인 경우 다음과 같은 정다면체를 구성할 수 있다.

• 정삼각형 3개 : 정사면체
• 정삼각형 4개 : 정팔면체
• 정삼각형 5개 : 정이십면체

정사각형

정삼각형과 비슷한 방법으로 다음과 같이 생각할 수 있다.

• 정사각형의 한 내각의 크기 : $90^\circ$
• 한 꼭짓점에 모일 수 있는 정사각형 개수 : 3, 4개
  • 3개 $\rightarrow$ 정다면체 가능성 있음
    (정육면체)
  • 4개 $\rightarrow$ 다면체 구성 불가
    $\because\;90^\circ\times 4 = 360^\circ$

정오각형

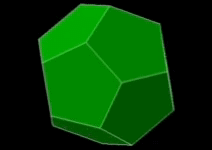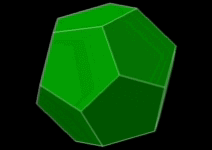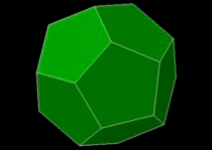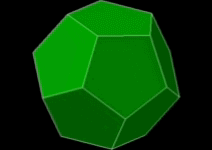
• 정오각형의 한 내각의 크기: $108^\circ$
• 한 꼭짓점에 모일 수 있는 정오각형의 개수: 3개
  • 3개 $\rightarrow$ 정다면체 가능성 있음
    (정십이면체)
  • 4개 $\rightarrow$ (볼록)다면체 구성 불가
    $\because\;108^\circ\times 4 >360^\circ$

정육각형, 정칠각형 $\cdots$

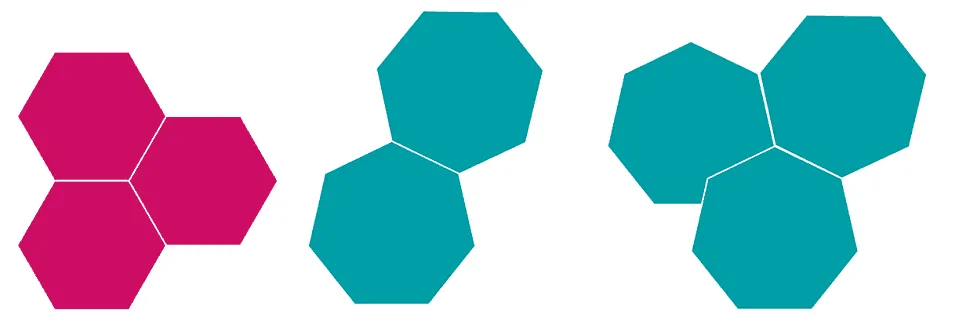
정육각형

• 정육각형의 한 내각의 크기: $120^\circ$
• 한 꼭짓점에 모일 수 있는 정육각형의 개수: 3개
  • 3개 $\rightarrow$ 구성불가
    $\because\;120^\circ \times 3=360^\circ$

정칠각형, 정팔각형$\cdots$에 대해서 생각해보자.

• 정$n$각형의 한 내각의 크기
  • $180^\circ-\dfrac{360}{n}$
  • 성질 : $n$이 커지면 한 내각의 크기가 점점 커진다.

정칠각형, 정팔각형 $\cdots$ 는 정육각형(한 내각 $120^\circ$)보다 한 내각의 크기가 더 크기 때문에 한 꼭짓점에 3개의 다면체가 모일 수 없다.

• 정다면체를 만들수 없다.

결론, 정리

위의 과정을 토대로 정다면체는 5개 뿐임을 알 수 있다.

정다면체의 꼭짓점, 모서리 개수

정사면체, 정팔면체, 정육면체의 경우는 꼭짓점과 모서리의 개수를 직접 셀 수 있다. 그렇다면 정십이면체와 정이십면체의 꼭짓점과 모서리의 개수는 어떻게 셀 수 있을까?

대칭적인 구조에서 개수를 세는 아이디어

• 규칙을 찾는다.
• 전체를 규칙적으로 센다.
• 중복을 고려한다.

꼭짓점 개수

정십이면체

• 규칙 : 한 면당 꼭짓점 $\colorbox{#ffff00}{5개}$
• 전체 : $\colorbox{#ffff00}{5개}\times \colorbox{#dcff8c}{12면}$
• 중복 : $\colorbox{#94feff}{3회}$ (한 꼭짓점에 모인 면의 개수)

$\therefore\; \dfrac{\colorbox{#ffff00}{5개}\times \colorbox{#dcff8c}{12면}}{\colorbox{#94feff}{3회}}=20\text{개}$

정이십면체

• 규칙 : 한 면당 꼭짓점 $\colorbox{#ffff00}{3개}$
• 전체 : $\colorbox{#ffff00}{3개}\times \colorbox{#dcff8c}{20면}$
• 중복 : $\colorbox{#94feff}{5회}$ (한 꼭짓점에 모인 면의 개수)

$\therefore\; \dfrac{\colorbox{#ffff00}{3개}\times \colorbox{#dcff8c}{20면}}{\colorbox{#94feff}{5회}}=12\text{개}$

모서리 개수

정십이면체

• 규칙 : 한 면당 모서리 $\colorbox{#ffff00}{5개}$
• 전체 : $\colorbox{#ffff00}{5개}\times \colorbox{#dcff8c}{12면}$
• 중복 : $\colorbox{#94feff}{2회}$ (한 모서리에 인접한 면의 개수)

$\therefore\; \dfrac{\colorbox{#ffff00}{5개}\times \colorbox{#dcff8c}{12면}}{\colorbox{#94feff}{2회}}=30\text{개}$

정이십면체

• 규칙 : 한 면당 모서리 $\colorbox{#ffff00}{3개}$
• 전체 : $\colorbox{#ffff00}{3개}\times \colorbox{#dcff8c}{20면}$
• 중복 : $\colorbox{#94feff}{2회}$ (한 모서리에 인접한 면의 개수)

$\therefore\; \dfrac{\colorbox{#ffff00}{3개}\times \colorbox{#dcff8c}{20면}}{\colorbox{#94feff}{2회}}=30\text{개}$

표 정리

오늘 학습한 내용을 표로 정리하고 마무리 하도록 하자.

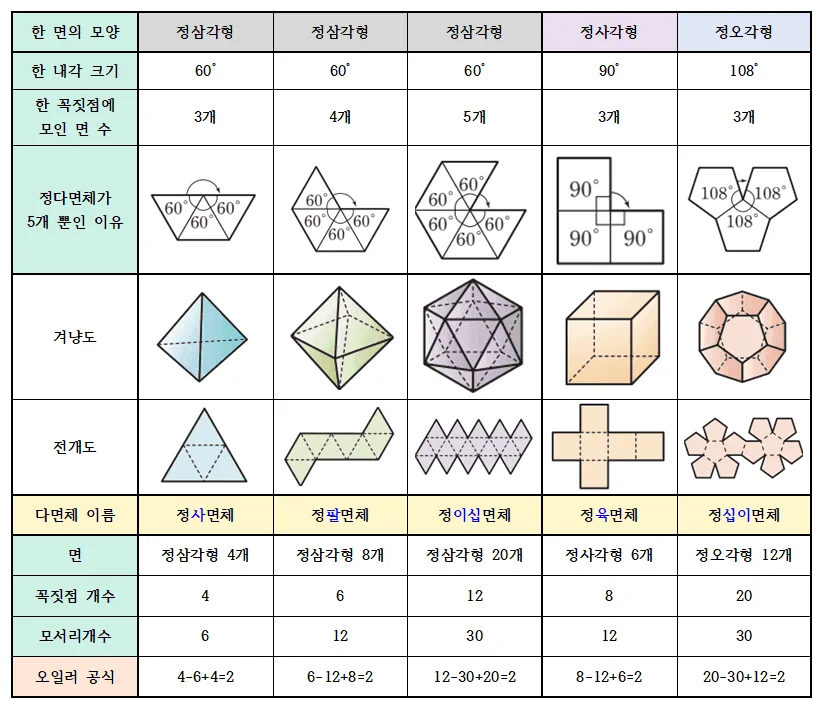
이상으로 정다면체의 종류가 5개 뿐인 이유와 정다면체의 꼭짓점과 모서리의 개수에 대한 학습을 마무리 하도록 하겠습니다.