수학에서 원과 직선이 이루는 각을 정확히 이해하면, 다양한 기하 문제를 한눈에 해결할 수 있습니다.
이번 시간에는 접선과 현이 이루는 각을 원주각을 이용해 정리하고, 이를 응용한 강력한 정리인 방멱정리(할선정리, 접선정리)에 대하여 알아보도록 하겠습니다.
이 내용은 중학교 기하 파트에서 반드시 이해하고 넘어가야 할 핵심 개념이며, 수능 기하 선택자나 수학 경시대회 준비자에게도 매우 유익한 내용이니 꼭 정리해 두길 바랍니다.
목차
학습목표
- 원주각을 이용하여 접선과 현이 이루는 각과 동일한 각을 찾을 수 있다.
- 방멱정리에 대해 설명할 수 있다.
복습
원주각과 중심각사이 관계 대한 내용을 학습하고 아래의 내용을 학습하길 바란다.
접선과 현이 이루는 각
원 $O$위의 서로 다른 두 점$A,B$와 점$A$를 지나는 접선 $l$에 대하여 $A,B$는 원을 두 호로 나누고, 접선 $l$은 현$\overline{AB}$와 만나 두 각 을 만든다. 접선과 현이 이루는 각 중 하나를 $a$라 할 때 다음이 성립한다.
- [$\angle{a}$ 내부의 호에 대한 원주각] $=a$
이는 접선과 현이 이루는 각에 따라 두 가지 경우로 나누어 보일 수 있다.
접선과 현이 이루는 각이 예각 일 때
접선 $l$과 현$\overline{AB}$와 이루는 예각 $\angle{BAC}=a$에 대하여 [$a$ 내부의 호에 대한 원주각] $=a$이다.
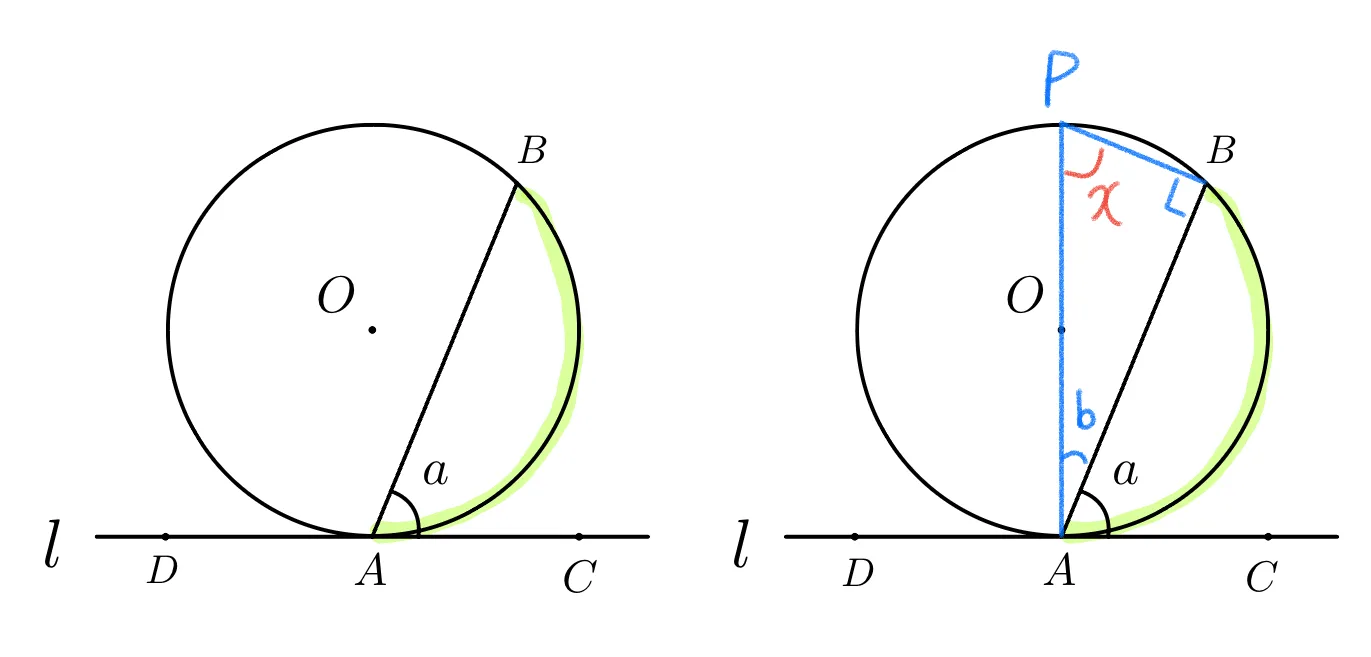
$\overparen{AB}$에 대한 원주각은 항상 일정하므로 $\overline{AP}$가 지름이 되는 점$P$에서 원주각($x$)이 $a$와 동일함을 보이면 충분하다.
- 지름 $\overline{AP}$에 대하여 $\angle{PAC}=a+b=90^{\circ}$,
- 반원에 대한 원주각 : $\angle{PBC}=90^{\circ}$ , $b+x=90^{\circ}$
- $\therefore x=a$
접선과 현이 이루는 각이 둔각 일 때
접선 $l$과 현$\overline{AB}$와 이루는 둔각 $\angle{BAD}=a$에 대하여 [$a$ 내부의 호에 대한 원주각] $=a$이다.
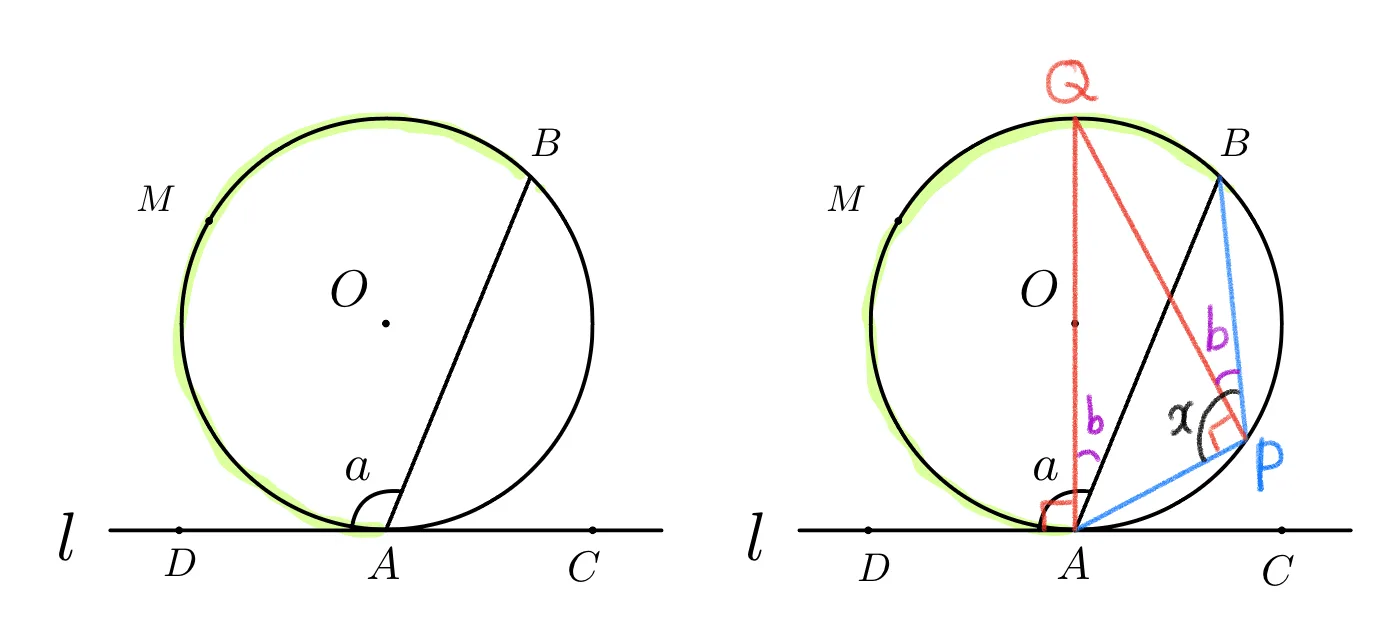
$\overparen{AMB}$에 대한 원주각은 항상 일정하므로 점$P$에서 원주각($x$)이 $a$와 동일함을 보이면 충분하다.
- $\angle{DAQ}=\angle{APQ}=90^{\circ}$
- $\overparen{QB}$의 원주각 : $\angle{QAB}=\angle{QPB}$
- $\therefore x=a$
방멱정리 (할선정리)
방멱 정리는 할선 정리 또는 접선 정리 라고한다. 먼저 방멱에 대하여 알아보고 방멱 정리를 학습해 보자. 할선정리를 증명하기 위해서는 중학교 2학년 닮음에 대한 학습이 필수적 입니다. 닮음에 대한 내용을 모른다면 아래 링크의 강의를 활용해 주세요.
방멱의 정의
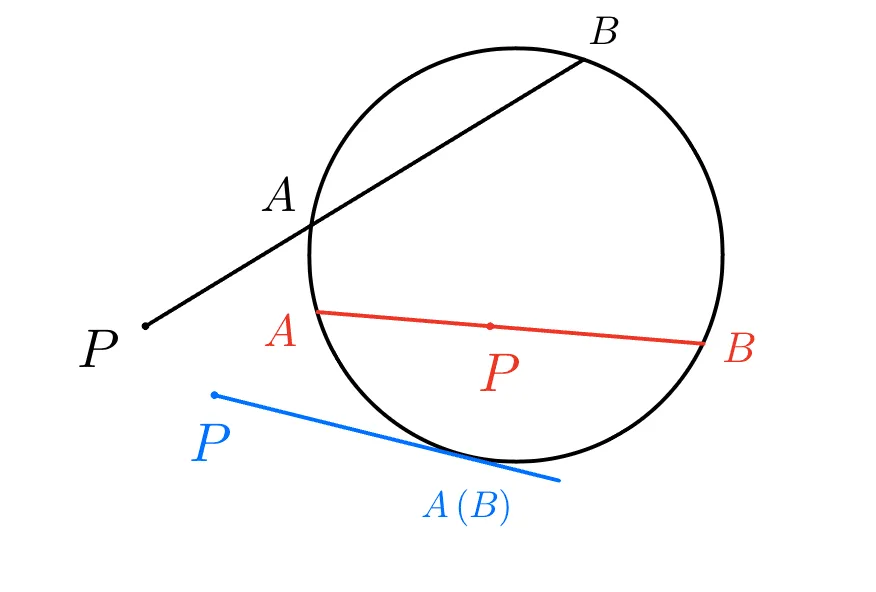
한 점 $P$를 지나는 직선이 원과 만나는 점을 $A,B$라고 할 때
- $\overline{PA}\times\overline{PB}$를 방멱이라고 한다.
- $A$에서 접하는 경우 방멱은 $\overline{PA}^2$이다.
두 현에 대한 방멱정리 증명1
원 내부에 한 점 $P$를 지나는 서로 다른 두 직선 $l,m$에 대하여 $l$ 과 $m$이 원과 만나는 두 점을 각각 $A,B$와 $C,D$라 하면 다음이 성립한다.
$\overline{PA}\times\overline{PB}=\overline{PC}\times\overline{PD}$
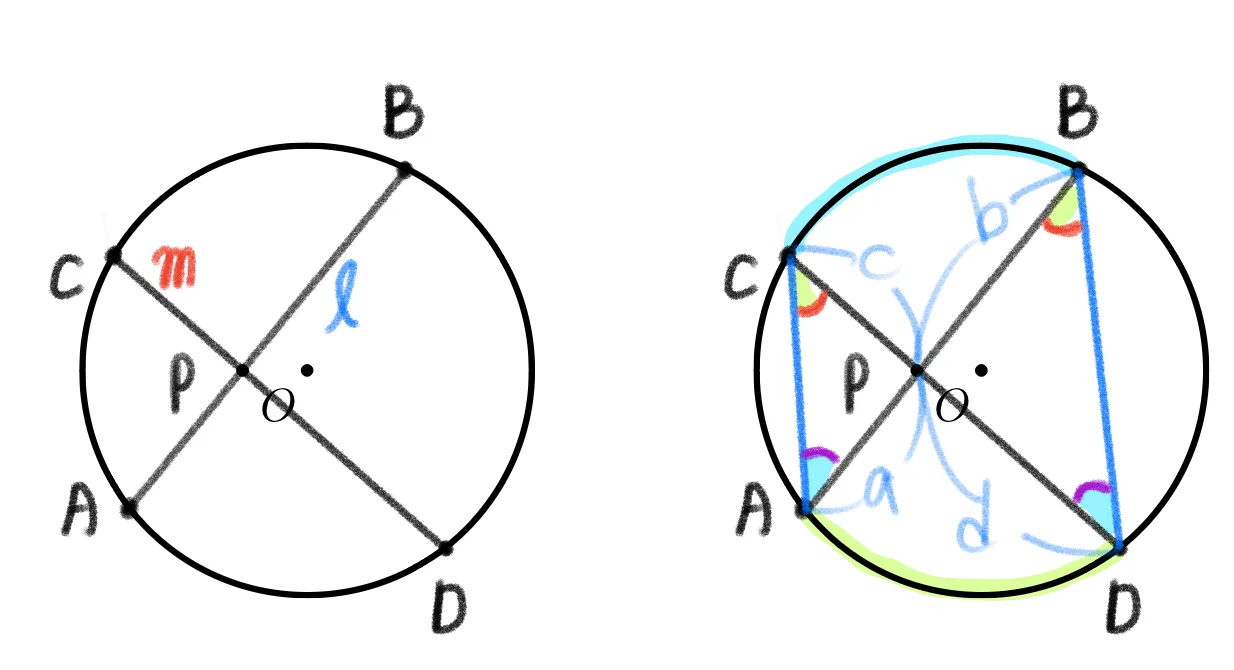
- $\overparen{AD}$의 원주각 : $\angle{ACD}=\angle{ABD}$
- $\overparen{CB}$의 원주각 : $\angle{CAB}=\angle{CDB}$
- $\triangle{PAC}\sm\triangle{PDB}$ 이고 닮음비에 의해 $ab=cd$
두 할선에 대한 방멱정리 증명2
원 밖의 한 점 $P$를 지나는 서로 다른 두 직선 $l,m$에 대하여 $l$ 과 $m$이 원과 만나는 두 점을 각각 $A,B$와 $C,D$라 하면 다음이 성립한다.
$\overline{PA}\times\overline{PB}=\overline{PC}\times\overline{PD}$
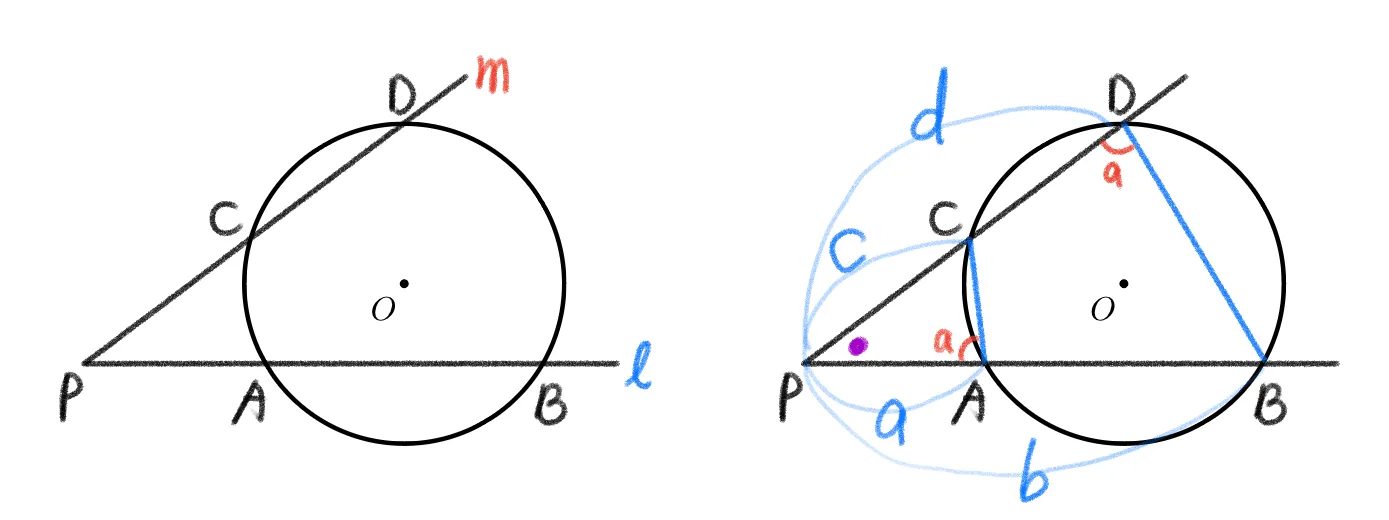
- $\square{ABDC}$는 원에 내접하므로 $\angle{PAC}=\angle{CDB}$
- $\triangle{PAC}\sm\triangle{PDB}$ 이고 닮음비에 의해 $ab=cd$
할선과 접선에 대한 방멱정리 증명3
원 밖의 한 점 $P$를 지나는 서로 다른 두 직선 $l,m$에 대하여 $l$이 원과 만나는 접점을 $A$, $m$이 원과 만나는 서로 다른 두 점을 $C,D$라 하면 다음이 성립한다.
- $\overline{PA}^2=\overline{PC}\times\overline{PD}$
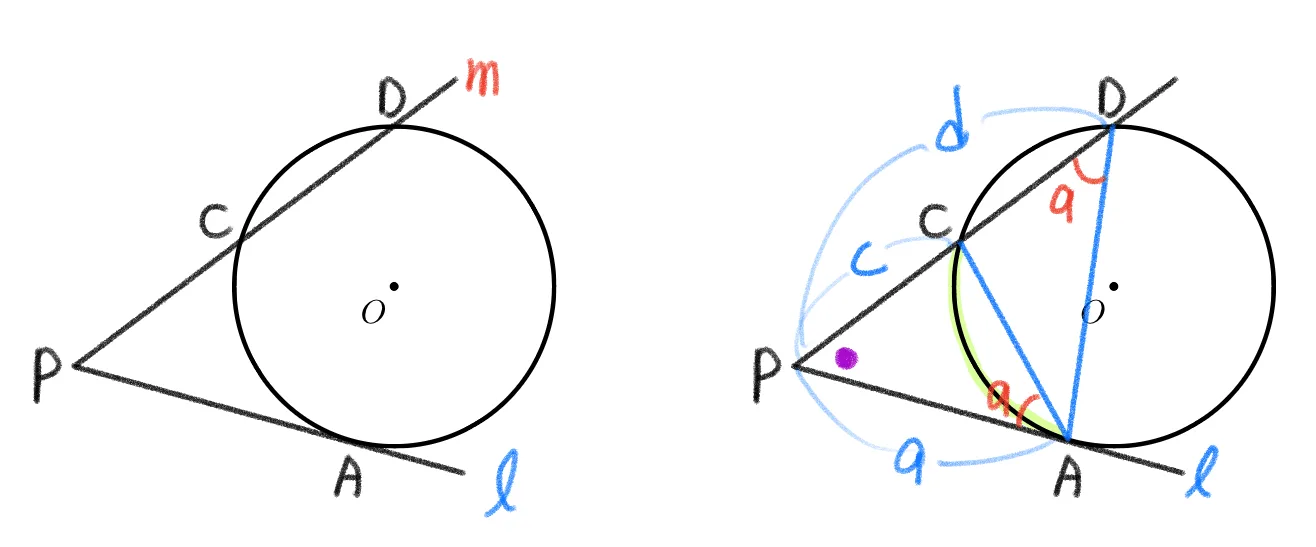
- 접선과 현이 이루는 각 : $\angle{CAP}=\angle{ADP}$
- $\triangle{PAC}\sm\triangle{PDA}$이고 닮음비에 따라 $a^2=cd$
마지막으로 이번 시간에 학습한 내용을 정리하고 마무리 하도록 하겠습니다.
정리
- [접선과 이 이루는 각]$=$[각 내부의 호에 대한 원주각}
- 원 내부의 한 점 $P$를 지나는 두 현에 대한 방멱의 값은 일치한다.
- 원 밖의 한 점 $P$를 지나는 두 할선에 대한 방멱의 값은 일치한다.
- 원 밖의 한 점 $P$를 지나는 접선과 할선에 대한 방멱의 값은 일치한다.
방멱의 정리를 할선정리라고 부르기도 한다.
