점 선 면의 위치관계는 공간도형을 이해하는데 중요한 개념이다. 이번 글에서는 도형의 위치관계를 체계적으로 정리하고 기하적 사고의 폭을 넓혀 보기로 하자.
목차
점 직선 평면의 위치관계 개요
점 선 면의 위치관계는 다음의 경우로 나누어 생각해 볼 수 있다.
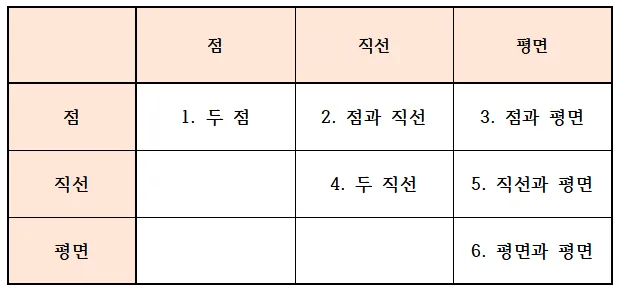
이제 부터 1~6까지 점 직선 평면 사이의 위치관계에 대해 하나씩 정리해 보기로 하자.
점과 기본도형의 위치관계
두 점 사이의 위치관계(1)
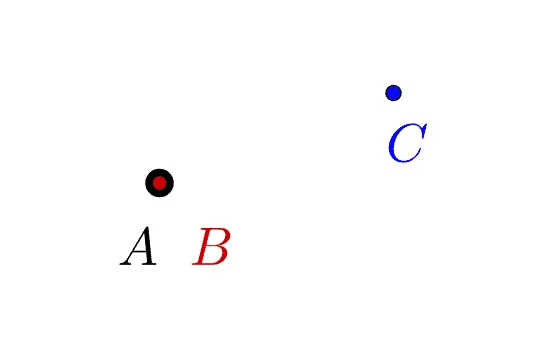
두 점 사이의 위치관계(1)는 서로 같거나 다른 두 경우 뿐이다.
- A, B : 서로 같은 두 점
- A, C : 서로 다른 두 점
점과 직선의 위치관계(2)
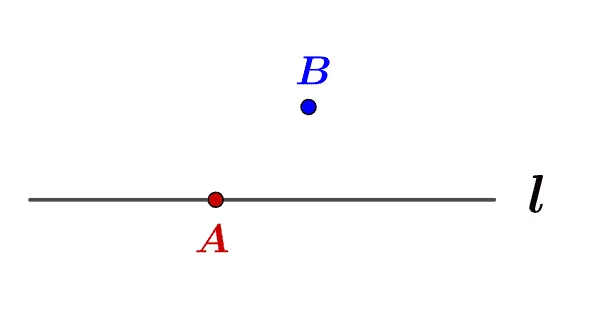
위의 그림을 통해 점과 직선의 위치관계를 정리하면 다음과 같다.
- 점 A는 직선 $l$위에 있다.
- 직선 $l$은 점A를 지난다.
- 점 B는 직선 $l$위에 있지 않다.
- 직선 $l$은 점B를 지나지 않는다.
수학에서 $\bbox[#ffff00]{\text{위에 있다}}$는 표현은 일상에서 사용하는 ‘위에있다’는 표현과 달리 주어진 도형에 포함되어 있음을 의미이다.
점과 평면의 위치관계(3)
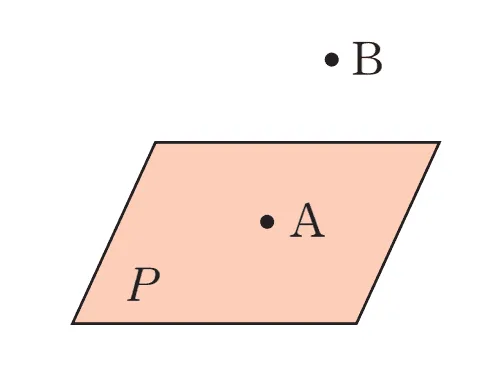
위의 그림을 통해 점과 평면의 위치관계는 다음과 같이 정리할 수 있다.
- 점A는 평면 P위에 있다.
- 점B는 평면 P위에 있지 않다.
두 직선의 위치관계(4)
두 직선의 위치관계를 평면과 공간에서 위치관계로 나누어 정리해 보자.
평면에서 두 직선의 위치관계
평면에서 두 직선은 만나거나 만나지 않는 경우로 나누어 생각하면 다음과 같이 정리할 수 있다.
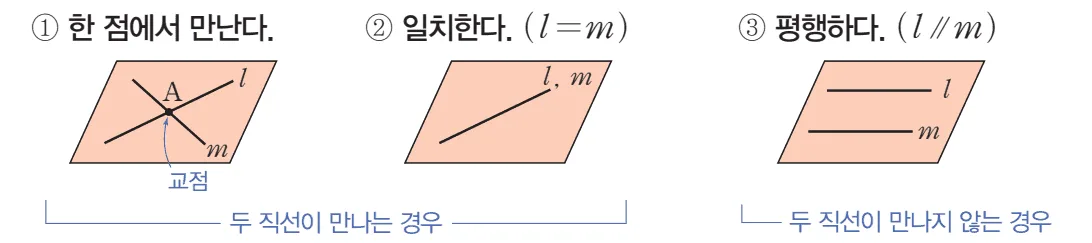
- 만나는 경우
- 한 점에서 만난다.
- 일치한다.
- 만나지 않는 경우
- 두 직선이 평행하다.
개념확인
평면에서 두 직선이 아래와 같이 주어질 때 두 직선의 위치관계에 대해 생각해 보자.
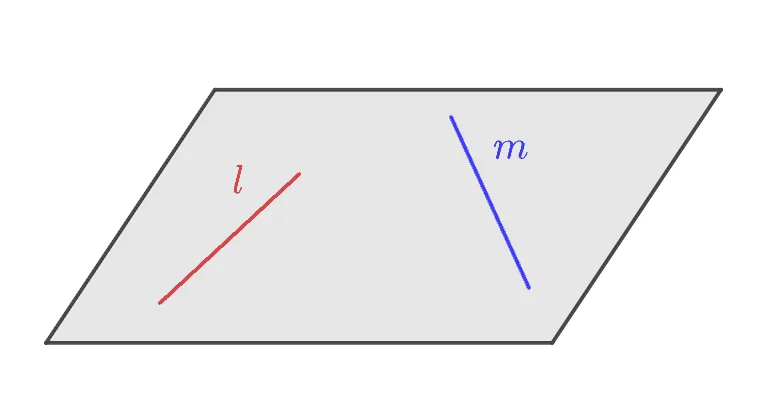
이 경우는 서로 만나지 않는 것처럼 보인다. 하지만 직선은 무한히 뻗어나가기 때문에 직선 $l,\; m$의 위치관계는 ‘한 점에서 만난다’ 이다.
공간에서 두 직선의 위치관계
공간은 평면을 3차원으로 확장한 개념이다. 따라서 평면에서 가능한 위치관계는 공간에서도 가능하다. 공간에서는 평면에서 존재 하지 않는 위치관계를 추가로 생각할 수 있다.
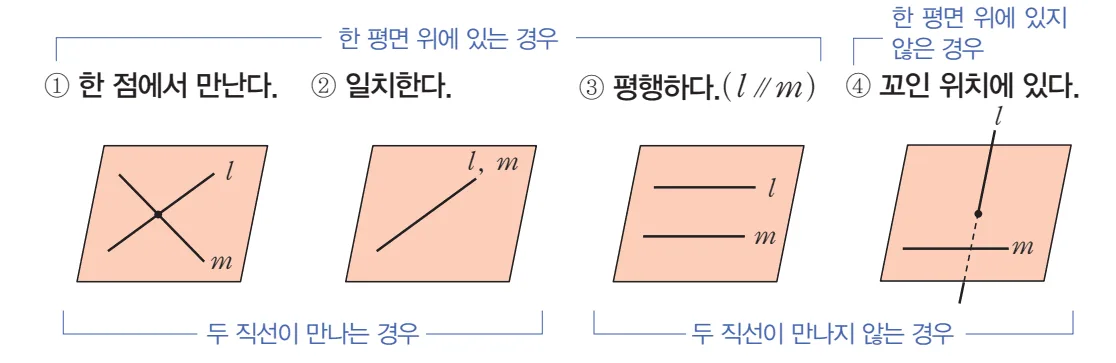
- 만나는 경우
- 한 점에서 만난다.
- 일치한다.
- 만나지 않는 경우
- 두 직선이 평행하다. (기호: $l\pam$)
- 꼬인위치
두 직선의 위치관계 정리
공간과 평면에서 위치관계를 하나의 표로 다음과 같이 정리할 수 있다.
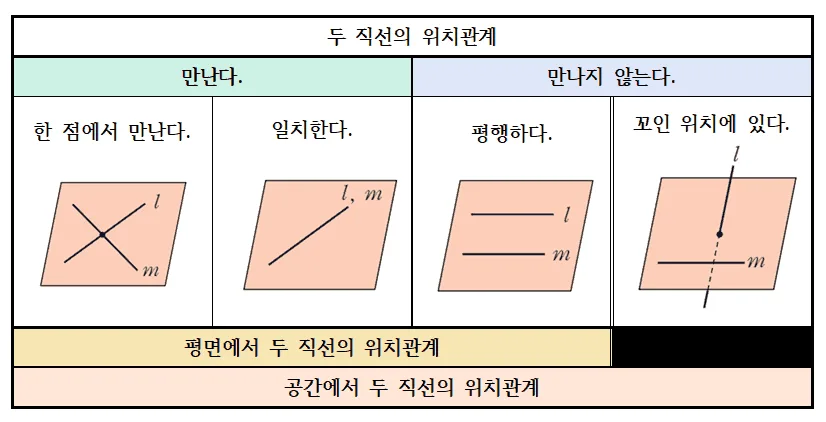
공간에서 직선과 평면의 위치관계(5)
이제 공간에서 직선과 평면의 위치관계를 그림으로 정리해 보기로 하자.
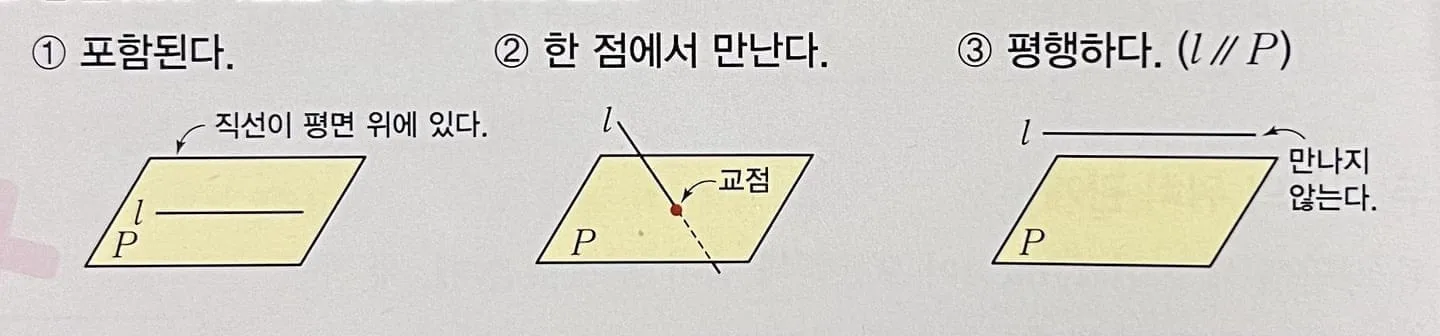
- 만나는 경우
- 직선이 평면에 포함된다. (직선이 평면 위에 있다.)
- 한 점에서 만난다.
- 만나지 않는 경우
- 평행하다. (기호: $l\paP$)
공간에서 두 평면의 위치관계(6)
마지막으로 공간에서 두 평면의 위치관계는 다음과 같이 정리할 수 있다.

- 만나는 경우
- 일치한다.
- 만난다.
- 만나지 않는 경우
- 평행하다. (기호: $P\paQ$)
평면의 결정조건(참고)
평면의 결정조건에 대해서도 정리해 보자.
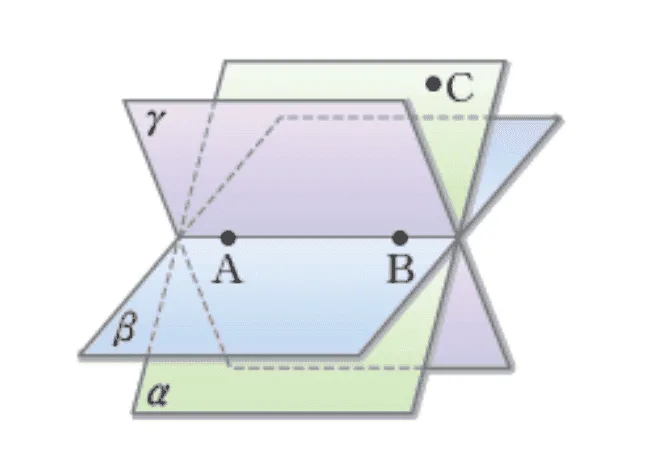
두 점 A, B를 지나는 평면은 무수히 많다. 따라서 평면을 하나로 결정 짓기 위한 조건은 다음과 같다.
- 한 직선 위에 있지 않은 세 점
$\overleftrightarrow{AB}$를 포함하는 평면도 무수히 많다. 따라서 평면을 하나로 결정 짓기 위한 조건은 다음과 같다.
- 한 직선과 그 직선 위에 있지 않은 한 점
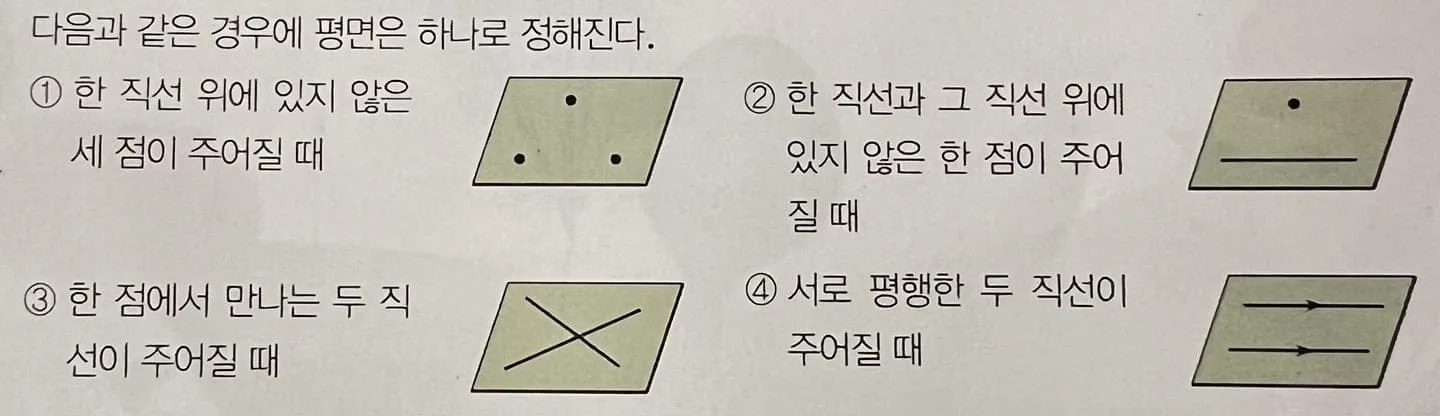
이 밖에도 평면의 결정 조건은 다양하게 생각할 수 있고 이를 정리하면 다음과 같다.
맺음말
이번 시간에는 점 선 면의 위치관계에 대해 학습하였습니다. 공식도 없고 간단해 보이지만 복잡한 문제를 풀어내는데 중요한 기초가 되므로 꼭 정확히 이해하고 설명할 수 있도록 학습하길 바랍니다.
