입체도형의 부피 공식, 증명, 카발리에리의 원리

이 글에서는 입체도형의 부피를 구하는 방법에 대해 정리하였습니다. 논리적인 설명을 위해 카발리에리의 원리를 사용하였고, 뿔의 부피가 기둥의 $\dfrac{1}{3}$임을 논리적으로 설명하였습니다.

카발리에리의 원리

카발리에리는 면은 무수히 많은 평행한 선분들로 구성되어 있고, 입체는 무수히 많은 평행한 면들로 구성된 것으로 간주하고 다음과 같은 사실을 발견하였다. (자료출처)

• 두 평면도형을 직선($l$) 위에 나란히 두고, $l$과 평행한 직선이 두 평면과 만나는 선분의 길이가 항상 같으면 두 평면도형의 넓이가 같다.
• 두 입체도형을 평면($P$)위에 올려두고, $P$와 평행한 평면이 두 입체도형과 만나는 단면의 넓이가 항상 같으면 두 입체도형의 넓이가 같다.

평면도형의 넓이

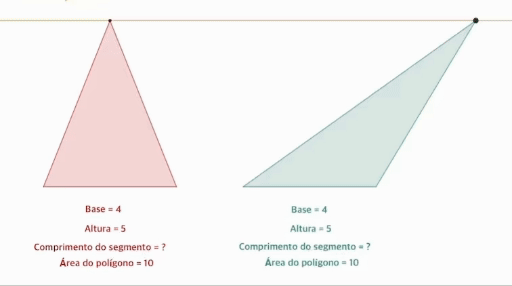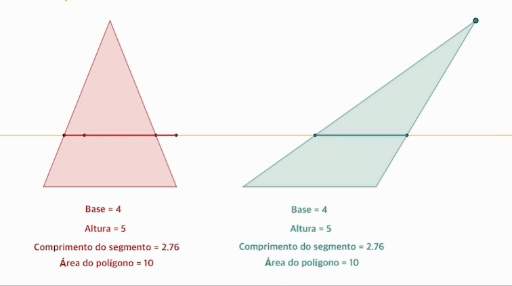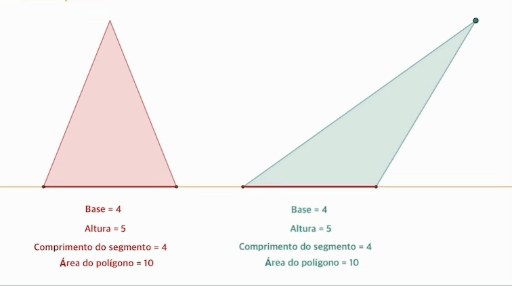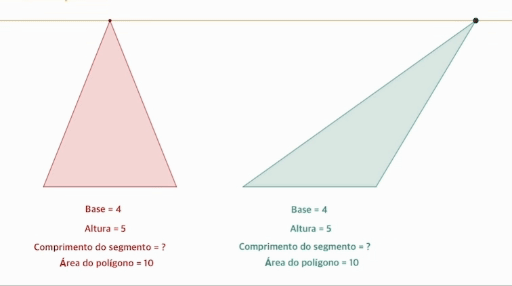
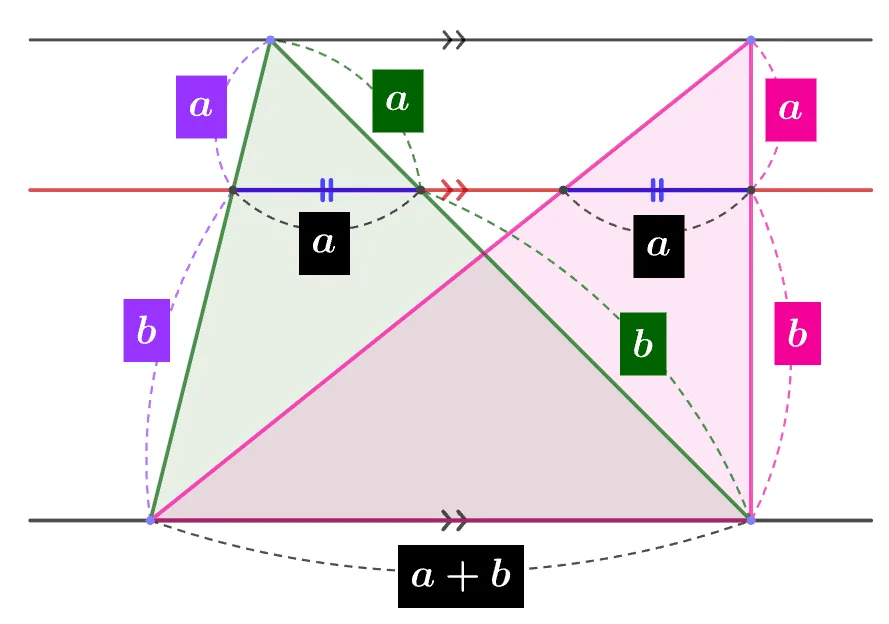
• 밑변의 길이가 같고 높이가 같은 두 삼각형은 넓이가 같다.
  • 직선 위의 두 삼각형에 대하여 평행한 직선을 그릴 때 두 선분의 길이는 항상 같기 때문.

입체도형의 부피

동전이 쌓인 원기둥에서 동전을 밀어도 부피는 바뀌지 않는다.

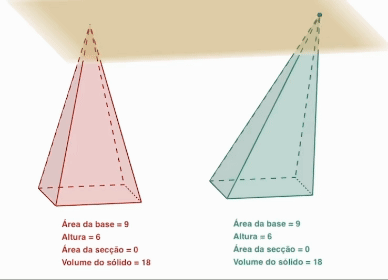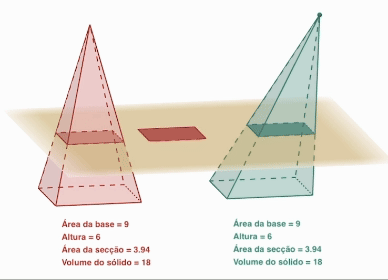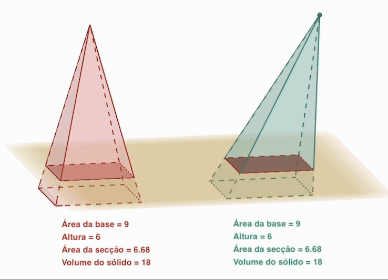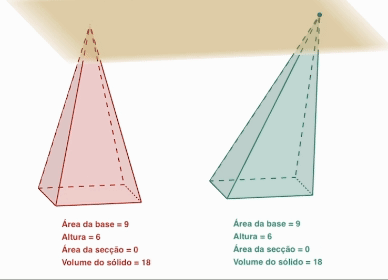
• 밑면이 합동이고 높이가 같은 각뿔과 빗각뿔의 부피는 같다.
  • 밑면이 합동이고 높이가 같은 뿔을 그림과 같이 평면으로 자르면 단면이 서로 합동이 된다.

입체도형의 부피 공식, 증명

부피는 가로, 세로, 높이가 1인 정육면체(cube)의 부피를 1이라 할 때, 입체도형의 상대적인 부피를 의미한다. 이를 이용하여 입체도형의 부피 공식을 정리해 보자.

기둥의 부피

$V_\text{기둥}=\bbox[#dcff8c]{\text{밑넓이}} \times \text{높이}$

각기둥의 부피

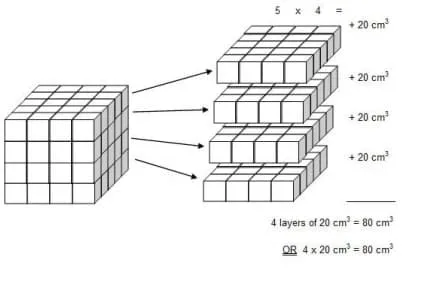
가로, 세로, 높이가 각각 $4,\;5,\;4$인 사각기둥의 부피를 구하는 과정은 다음과 같다.

• 기준 정육면체(cube) 부피: $1\times 1\times 1=\bbox[#ffc5fd]{1}$
• 사각기둥의 부피=$\bbox[#ffc5fd]{\text{cube}}$개수
  • $\bbox[#ffc5fd]{1}\times \bbox[#ffff00]{4\times5\times\times4}=80$

위 사실을 통해 사각기둥의 부피는 다음과 같이 정리할 수 있다.

\begin{align} V_\text{사각기둥}&=\bbox[#dcff8c]{\text{가로} \times \text{세로}} \times \text{높이}\\
&=\bbox[#dcff8c]{\text{밑넓이}} \times \text{높이}
\end{align}

사각기둥 뿐 아니라 n각기둥의 부피는 다음과 같이 구할 수 있다.

$V_\text{사각기둥}==\bbox[#dcff8c]{\text{밑넓이}} \times \text{높이}$

원기둥의 부피

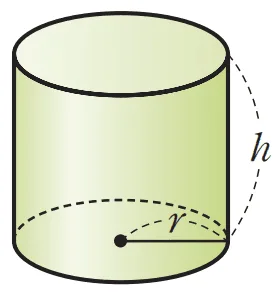
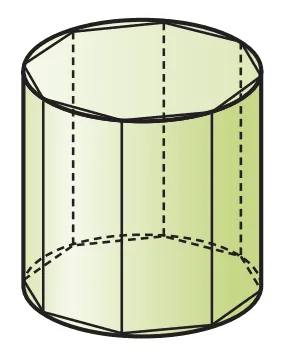
원기둥의 내부에 꼭 맞는 n각기둥을 생각하고 n을 늘려가면 각기둥은 원기둥에 가까워 진다. 따라서 직관적으로 다음과 같이 정리하자.

• $n$이 커질 수록 $V_\text{n각기둥} \approx V_\text{원기둥}$
  $\approx$ : ‘근사한다’는 표현
• 따라서 원기둥의 부피도 각기둥처럼 $\bbox[#dcff8c]{\text{밑면의 넓이}} \times \text{높이}$로 구할 수 있다.

밑면의 반지름이 $r$이고 높이가 $h$인 원기둥의 부피 공식은 다음과 같다.

\begin{align}V_\text{원기둥}&=\bbox[#dcff8c]{\text{밑넓이}}\times \text{높이}\\
&=\bbox[#dcff8c]{\pi r^2}\times h\end{align}

뿔의 부피

뿔의 부피는 밑면이 합동이고 높이가 같은 기둥의 부피의 $\dfrac{1}{3}$이다.

\begin{align}\bbox[#ffff00]{V_\text{뿔}}=\dfrac{1}{3}\times \bbox[#dcff8c]{V_\text{기둥}}\end{align}

각뿔의 부피

삼각기둥과 삼각뿔의 부피 관계

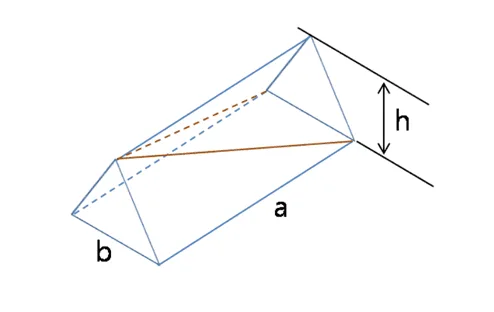
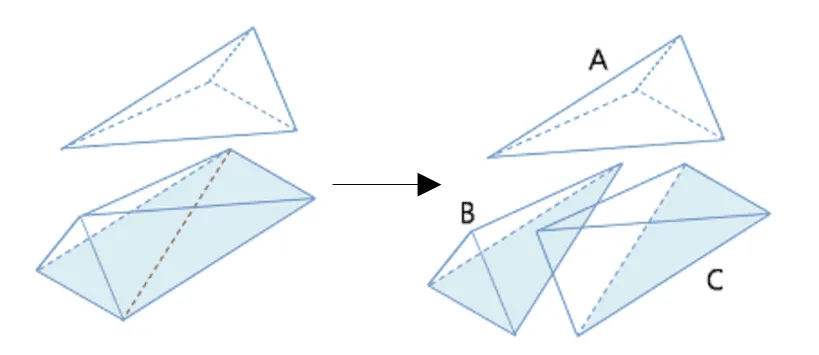
• (삼각기둥의 부피)$= V_A+V_B+V_C$
  • 밑면과 높이가 동일한 뿔에 카발리에리의 원리를 적용
    $V_A=V_B$, $V_B=V_C$
    $\therefore\; V_A=V_B=V_C$

따라서 삼각뿔 부피($\bbox[#ffff00]{V_\text{삼각뿔}}$)는 밑면이 합동이고 높이가 같은 삼각기둥의 부피($\bbox[#dcff8c]{V_\text{삼각기둥}}$)의 $\dfrac{1}{3}$이다.

\begin{align} \bbox[#ffff00]{V_\text{삼각뿔}}=\dfrac{1}{3}\times \bbox[#dcff8c]{V_\text{삼각기둥}}\end{align}

n각기둥과 n각뿔의 부피 관계

일반적인 각기둥과 각뿔의 부피도 비슷한 방법으로 보일 수 있기 때문에 오각기둥과 오각뿔에 대하여 보이기로 하자.

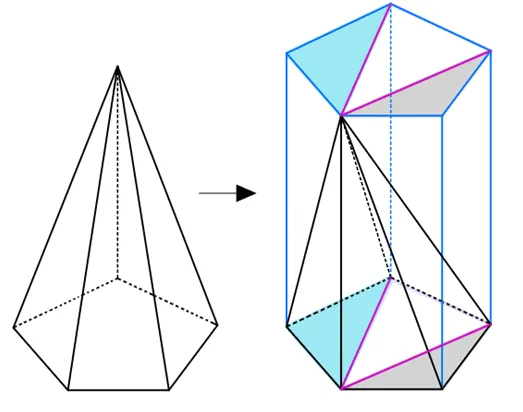
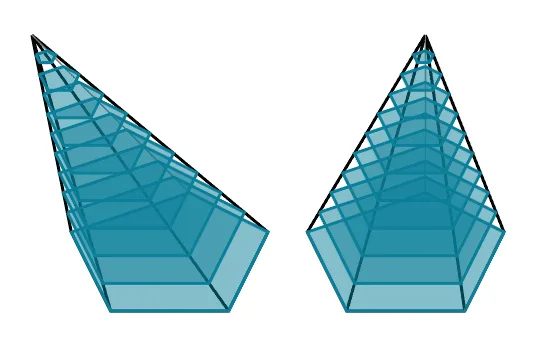
주어진 오각뿔의 부피는 기둥 속의 빗각뿔의 부피와 같다. 오각기둥을 삼각기둥 세 개로 자르면 빗각뿔은 삼각뿔 새 개로 잘린다. 따라서 다음과 같이 정리할 수 있다.

\begin{align} V_{\triangle \text{뿔1}}&=\dfrac{1}{3}\times V_{\triangle \text{기둥1}}\\
V_{\triangle \text{뿔2}}&=\dfrac{1}{3}\times V_{\triangle \text{기둥2}}\\
\bigoplus \quad V_{\triangle \text{뿔3}}&=\dfrac{1}{3}\times V_{\triangle \text{기둥3}}\\
\hline
V_{\text{오각빗각뿔}}&=\dfrac{1}{3}\times V_{\text{오각기둥}}
\end{align}

$\therefore \; V_\text{오각뿔}=V_\text{오각빗각뿔}=\dfrac{1}{3}\times V_{\text{오각기둥}}$

따라서 $n$각뿔의 부피($\bbox[#ffff00]{V_\text{n각뿔}}$)는 $n$각기둥의 부피($\bbox[#dcff8c]{V_\text{n각기둥}}$)의 $\dfrac{1}{3}$이다.

\begin{align} \bbox[#ffff00]{V_\text{n각뿔}}=\dfrac{1}{3}\times \bbox[#dcff8c]{V_\text{n각기둥}}\end{align}

원뿔의 부피

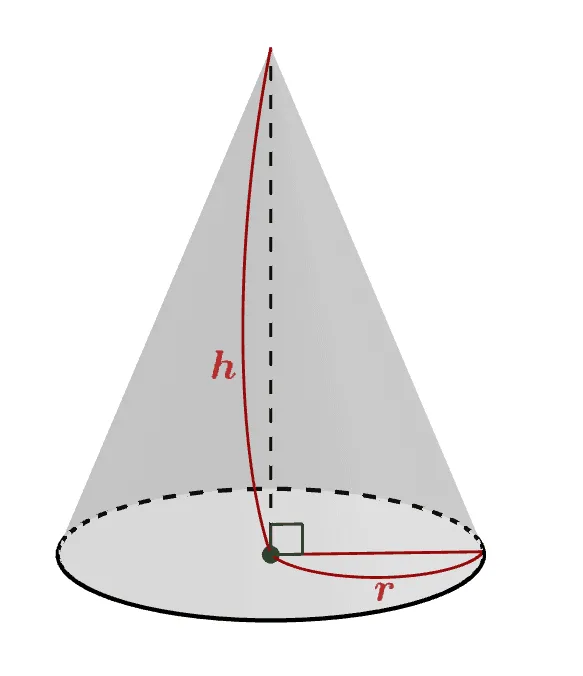
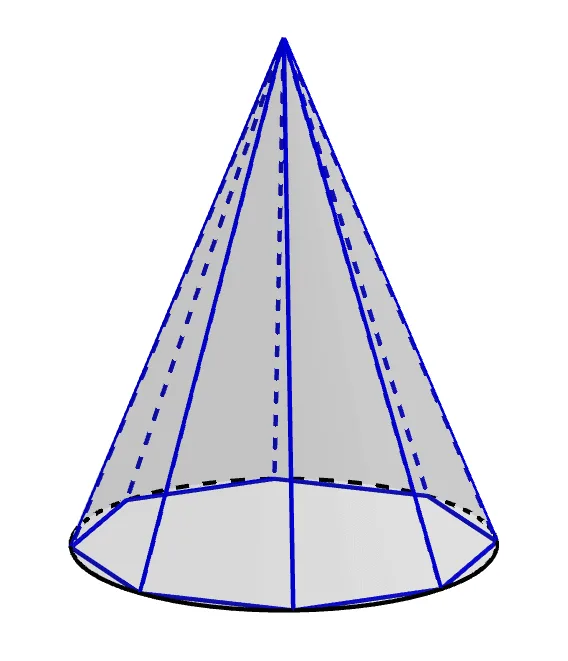
위와 같이 원뿔의 부피는 각뿔에 근사할 수 있다.

• $n$이 커질 수록 $V_\text{n각뿔} \approx V_\text{원뿔}$
  $\approx$ : ‘근사한다’는 표현
• 따라서 원뿔의 부피도 각뿔의 부피처럼 $\dfrac{1}{3}\times \bbox[#dcff8c]{V_\text{기둥}}$을 이용해 계산할 수 있다.

밑면의 반지름이 $r$이고 높이가 $h$인 원뿔의 부피는 다음과 같다.

\begin{align}\bbox[#ffff00]{V_\text{원뿔}}&=\dfrac{1}{3} \times \bbox[#dcff8c]{V_\text{원기둥}}\\
&=\dfrac{1}{3}\times \bbox[#dcff8c]{\pi r^2 h}\end{align}

뿔대의 부피

각뿔대, 원뿔대의 부피는 큰 뿔의 부피에서 잘려나간 뿔의 부피를 빼서 구할 수 있다.

\begin{align}V_\text{뿔대}=V_\text{큰뿔}-V_\text{작은뿔}\end{align}

뿔대의 부피 예제

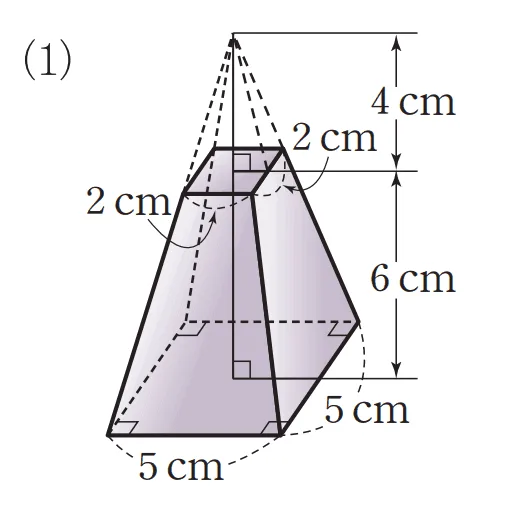
[1] 각뿔대의 부피

\begin{align} V_\text{뿔대}&=\bbox[#ffff00]{V_\text{큰뿔}}-\bbox[#dcff8c]{V_\text{작은뿔}}\\
&=\bbox[#ffff00]{\dfrac{1}{3}\times 5^2 \times 10}-\bbox[#dcff8c]{\dfrac{1}{3}\times 2^2 \times 4}\\
&=\dfrac{1}{3}\times 2 \{125-8\}\\
&=78(cm^3)\end{align}

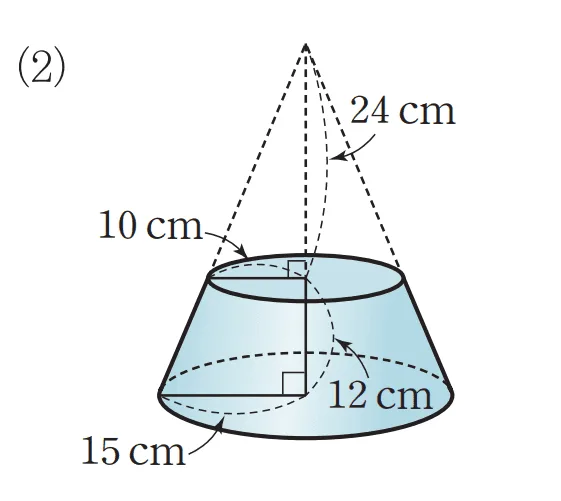
[2] 원뿔대의 부피

\begin{align} V_\text{뿔대}&=\bbox[#ffff00]{V_\text{큰뿔}}-\bbox[#dcff8c]{V_\text{작은뿔}}\\
&=\bbox[#ffff00]{\dfrac{1}{3}\times 15^2 \pi \times 36}-\bbox[#dcff8c]{\dfrac{1}{3}\times 10^2 \pi \times 24}\\
&=\dfrac{\pi}{3}\{15^2\times 36-10^2 \times 24 \}\\
&=\dfrac{1}{3}\times 5^2 \times 12 \times \pi \{27-8\}\\
&=1900\pi(cm^3)\end{align}

구의 부피

구의 표면에 서로 수직인 가로 세로 직선을 그리고 표면의 사각형과 중심을 연결한 도형에 대해 생각해보자.

• 구의 부피 공식 설명 자료 (영어, 유튜브)

구의 부피 공식 증명

조각이 작아질 수록 조각은 사각뿔에 근사한다. 따라서 다음과 같이 구의 부피를 구할 수 있다.

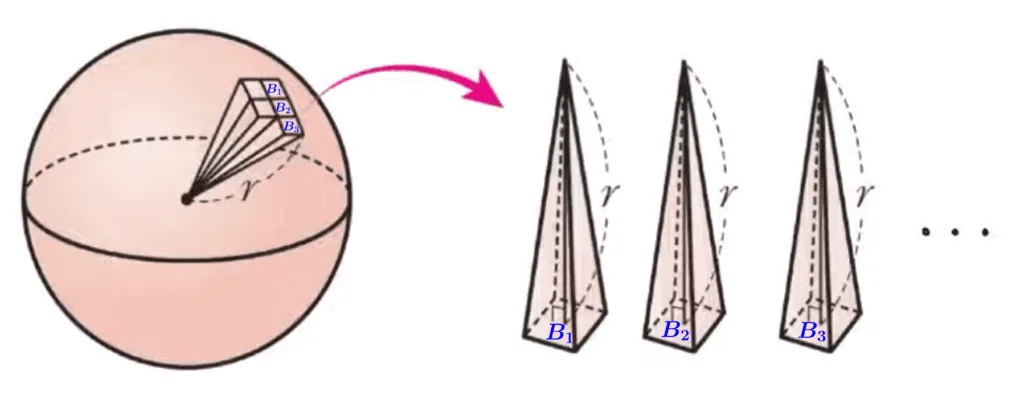
$V_\text{구의부피}=V_\text{뿔의부피 합}$

\begin{align} V&_\text{뿔의부피 합}\\[0.5em]
&=\dfrac{B_1r}{3}+\dfrac{B_2 r}{3}+\dfrac{B_3 r}{3}+\cdots+\dfrac{B_n r}{3}\\
&=\dfrac{r}{3}\{\bbox[#ffff00]{B_1+B_2+B_3+\cdots+B_n}\}\\
&=\dfrac{r}{3}\times \bbox[#ffff00]{S_\text{구}}\;(S_\text{구} : \text{구의 겉넓이})\\
&=\dfrac{r}{3}\times \bbox[#ffff00]{4 \pi r^2}\\
&=\dfrac{4}{3} \pi r^3\end{align}

이상으로 입체도형의 부피에 대한 정리를 마치도록 하겠습니다.