이번 포스팅에서는 입체도형의 겉넓이를 쉽게 이해할 수 있도록 기둥, 뿔, 구 등 다양한 도형의 겉넓이 공식을 체계적으로 설명하였습니다. 삼각형, 사다리꼴 등의 기본 도형부터 원기둥과 원뿔대까지 입체 도형의 겉넓이를 구하는 과정과 공식을 체계적으로 정리하는 시간이 되길 바랍니다.
목차
도형의 넓이 (기초이론)
가로 세로의 길이가 1인 정사각형(Square)의 넓이를 1이라 할 때 직사각형의 넓이는 다음과 같다.
- (가로)$\times $(세로)$=a\times b$
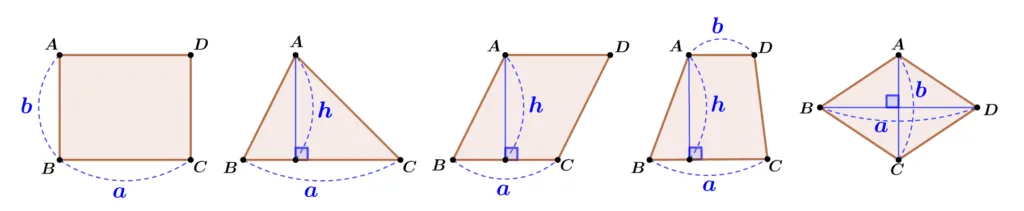
나머지 네 도형의 넓이를 직사각형의 넓이를 이용해 살펴보자.
도형의 넓이 증명
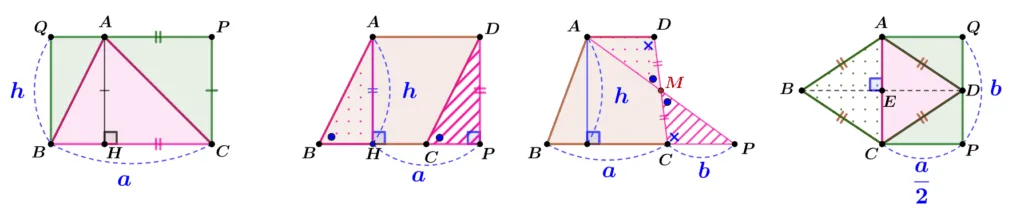
삼각형의 넓이
$\overline{BC}$를 한 변으로 하는 직사각형 $\square{QBCP}$에 대하여
$\triangle{AHC}\equiv \triangle{APC}$ (SAS합동)이고 비슷한 방법으로 $\triangle{ABH}\equiv \triangle{BAQ}$이다.
\begin{align}\therefore \; \triangle{ABC}=\dfrac{1}{2} \square{QBCP}=\dfrac{1}{2}ah\end{align}
평행사변형의 넓이
평행사변형의 점 $P$에서 $\overline{BC}$의 연장선 내린 수선의 발 $P$에 대하여 다음이 성립한다.
$\triangle{ABH}\equiv \triangle{DCP}$ (ASA 합동)
\begin{align}\therefore\;\square{ABCD}=\square{AHPD}=a h\end{align}
사다리꼴의 넓이
사다리꼴의 꼭짓점 $A$에서 변 $\overline {CD}$의 중점 $M$을 지나는 직선이 $\overline{BC}$의 연장선과 만나는 교점 $P$에 대하여 다음이 성립한다.
$\triangle{MDA}\equiv \triangle{MCP}$ (ASA 합동)
\begin{align}\therefore\; \square{ABCD}=\triangle{ABP}=\dfrac{1}{2}(a+b)h\end{align}
마름모의 넓이
[마름모의 성질]
$\overline{AC}$, $\overline{BD}$는 서로를 수직 이등분한다.
[step1] 마름모의 대변은 서로 평행하다.(평행사변형)
$\triangle{ABC}\equiv \triangle{ADC}$ (SSS 합동)
$\angle{BAC}=\angle{DCA}$ (엇각)
따라서 $\overline{AB}\pa\overline{CD}$ 이다.
[step2] 대각선이 서로를 이등분한다.(평행사변형의 성질)
$\triangle{ABE}\equiv \triangle{CDE}$ (ASA 합동)
$\overline{AE}=\overline{CE}$ (대응변)
[step3] 대각선이 서로 수직이다.
$\triangle{DAE}\equiv \triangle{DCE}$ (SSS 합동)
$\triangle{ABE}\equiv \triangle{BCE}\equiv \triangle{CDE}\equiv \triangle{DAE}$
$\therefore\; \overline{AC}\perp \overline{BD}$
[step1,2,3]에 의해 마름모의 대각선은 서로를 수직이등분한다.
따라서 마름모의 넓이 공식은 다음과 같다.
\begin{align}\square{ABCD}=\square{ACPQ}=\dfrac{1}{2} a b\end{align}
평면도형의 넓이 강의
평면도형의 넓이에 대한 내용이 정리되어 있지 않다면 아래의 링크를 이용해 초등학교 강의를 무료로 들을 수 있습니다.
입체도형의 겉넓이
기둥의 겉넓이
기둥은 합동인 두 밑면과 옆면으로 구성되어 있다 따라서 겉넓이는 다음과 같이 구할 수 있다.
- 겉넓이 : $(\bbox[#ffff00]{\text{밑넓이}})\times 2 +(\bbox[#ffc5fd]{\text{옆넓이}})$
- $(\bbox[#ffff00]{\text{밑넓이}})$ : 밑면의 넓이를 의미
- $(\bbox[#ffc5fd]{\text{옆넓이}})$ : (밑면의 둘레)$\times$(높이)
각기둥의 겉넓이
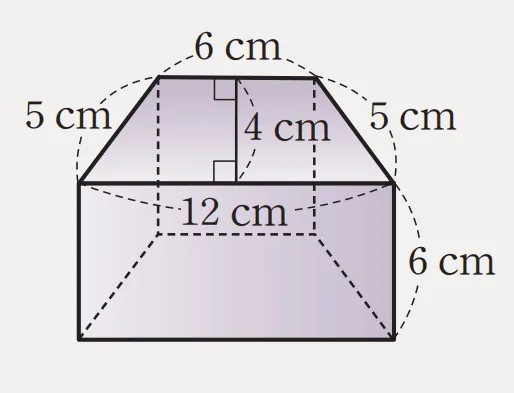
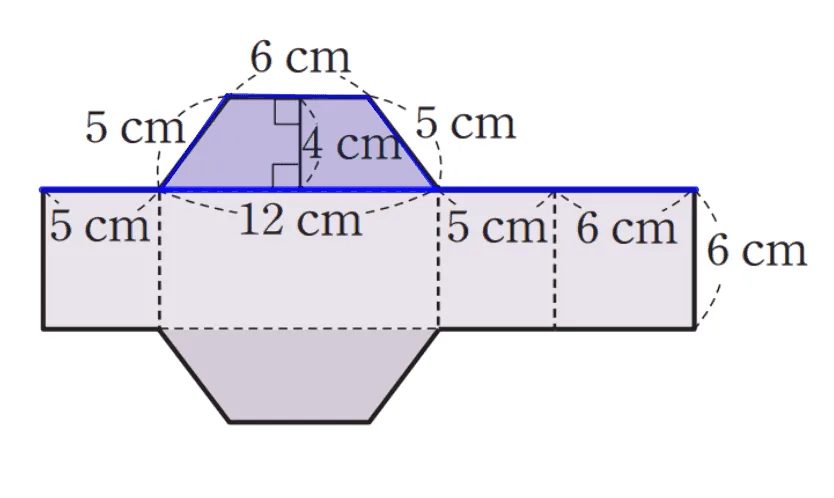
밑면이 사다리꼴인 각기둥의 겉넓이는 다음과 같이 구할 수 있다.
- 밑넓이: $\dfrac{1}{2}\times (6+12)\times 4=36cm^2$
- 옆넓이
\begin{flalign}&5\times 6+12 \times 6+5\times 6+6\times 6&\\[0.5em]
&=(\textcolor{blue}{5+12+5+6})\times 6&\\[0.5em]
&\quad \textcolor{blue}{\text{밑면의 둘레}}&\\[0.5em]
&=168cm^2&\end{flalign} - 겉넓이: $36\times 2+168=240cm^2$
원기둥의 겉넓이
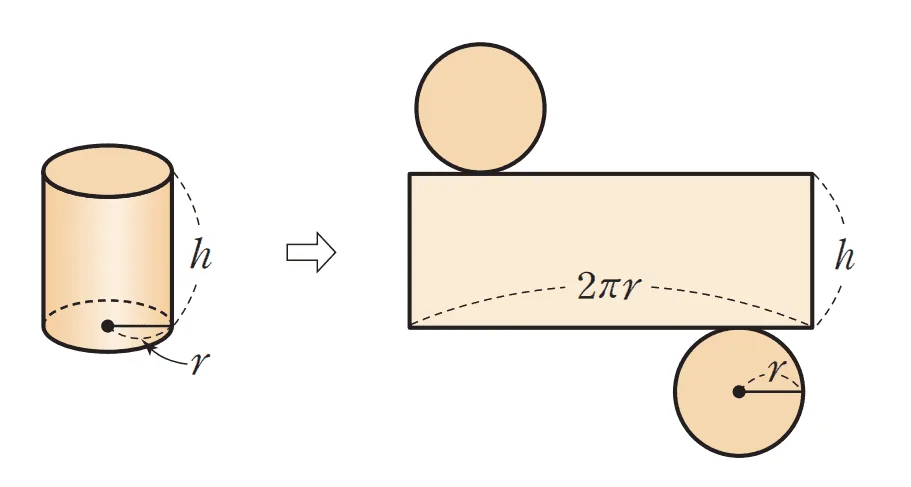
밑면의 반지름이 $r$이고 높이가 $h$인 원기둥에 대하여 다음이 성립한다.
- $(\bbox[#ffff00]{\text{밑넓이}})$: $\pi r^2$
- $(\bbox[#ffc5fd]{\text{옆넓이}})$: $\textcolor{blue}{2\pi r}h $ ($\textcolor{blue}{\text{밑면의 둘레}}$)
- 겉넓이: $\bbox[#ffff00]{\pi r^2} \times 2 + \bbox[#ffc5fd]{\textcolor{blue}{2\pi r} h}$
뿔의 겉넓이
뿔은 하나의 밑면과 옆면으로 구성되어 있으므로 다음과 같이 구할 수 있다.
- 겉넓이 : $(\bbox[#ffff00]{\text{밑넓이}})+(\bbox[#ffc5fd]{\text{옆넓이}})$
각뿔의 겉넓이
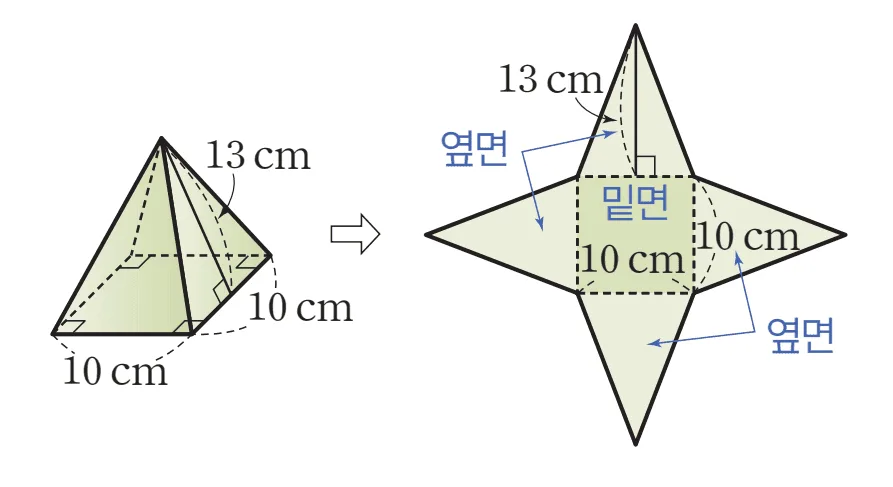
밑면은 한 변의 길이가 $10cm$인 정사각형이고, 옆면은 합동이고 높이가 $13cm$인 삼각형으로 구성된 사각뿔의 겉넓이는 다음과 같이 구할 수있다.
- $(\bbox[#ffff00]{\text{밑넓이}})=10 \times 10=100(cm^2)$
- $(\bbox[#ffc5fd]{\text{옆넓이}})=\dfrac{1}{2} \times 10\times 13\times 4$$=260(cm^2)$
- 겉넓이 : $\bbox[#ffff00]{100(cm^2)}+\bbox[#ffc5fd]{260(cm^2)}$
원뿔의 겉넓이
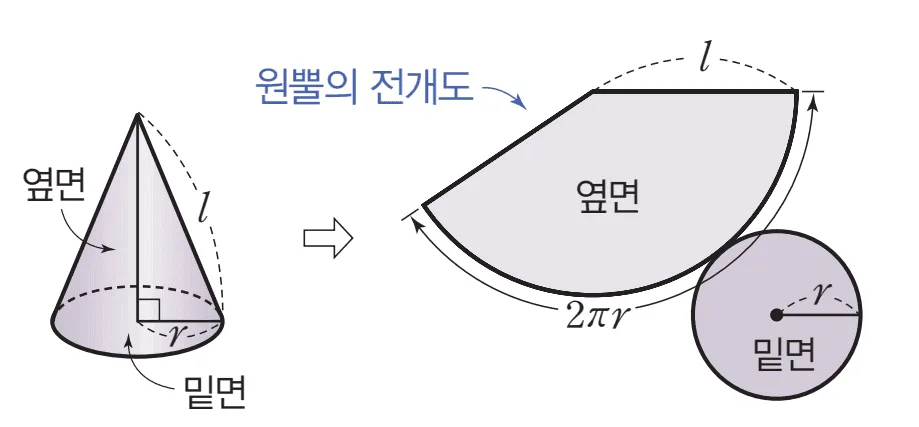
밑면의 반지름이 $r$이고, 모선의 길이가 $l$인 원뿔의 겉넓이는 다음과 같이 구할 수 있다.
- $(\bbox[#ffff00]{\text{밑넓이}})=\pi r^2$
- $(\bbox[#ffc5fd]{\text{옆넓이}})=\dfrac{2\pi r}{2}l$
- 겉넓이 : $\bbox[#ffff00]{\pi r^2}+\bbox[#ffc5fd]{\dfrac{2\pi r}{2}l}$
뿔대의 겉넓이
뿔대는 크기가 다른 두 밑면과 옆면으로 구성되므로 겉넓이는 다음과 같이 구할 수 있다.
- 겉넓이: $(\bbox[#ffff00]{\text{두 밑넓이 합}})+(\bbox[#ffc5fd]{\text{옆넓이}})$
각뿔대의 겉넓이
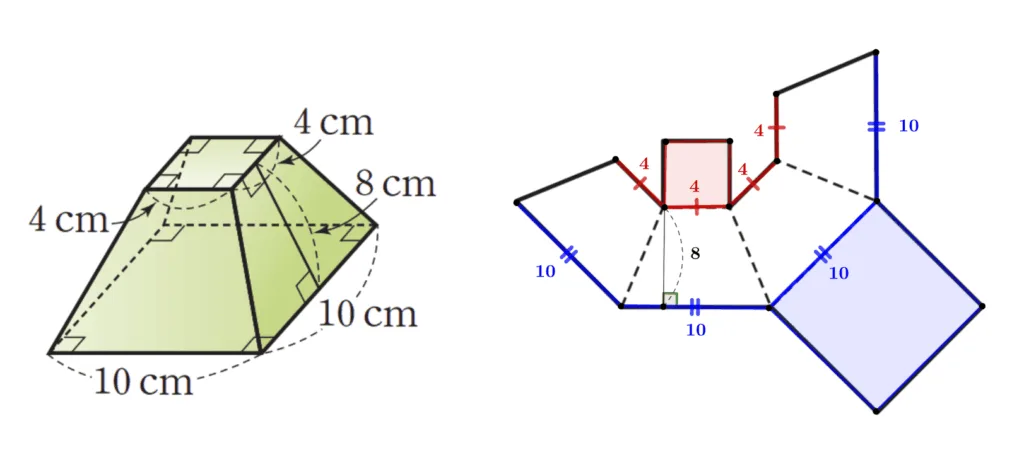
한 변이 길이가 $4cm,\; 10cm$인 정사각형을 밑면으로 하는 사각 뿔대의 겉넓이를 구해보자.
- $(\bbox[#ffff00]{\text{두 밑넓이 합}})=4^2 +10^2=116(cm^2)$
- $(\bbox[#ffc5fd]{\text{옆넓이}})$
- 사다리꼴: $\dfrac{1}{2}\times (4+10)\times 8=56(cm^2)$
- $(\bbox[#ffc5fd]{\text{옆넓이}})=56 \times \textcolor{blue}{4}=224(cm^2)$
- 겉넓이 : $\bbox[#ffff00]{116}+\bbox[#ffc5fd]{224}=3404(cm^2)$
원뿔대의 겉넓이
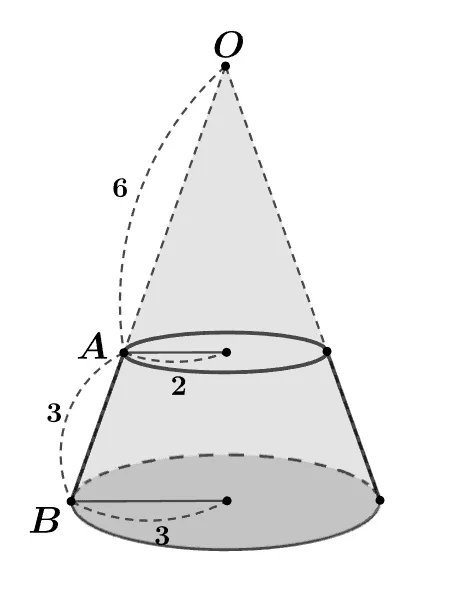
두 밑면의 반지름이 각각 $2, 3$이고 모선의 길이가 3인 원뿔대의 겉넓이를 구하는 방법을 정리해 보자.
- $(\bbox[#ffff00]{\text{두 밑넓이 합}})=4\pi +9\pi=13\pi$
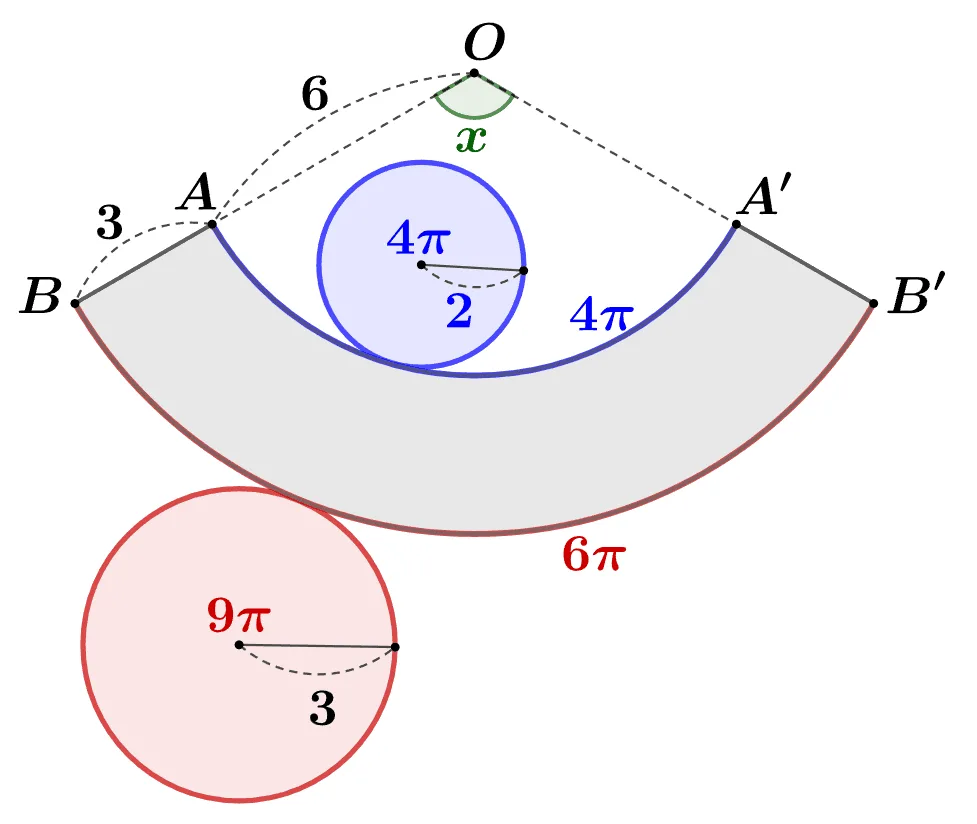
- $(\bbox[#ffc5fd]{\text{옆넓이}})$ 두 가지 방법
- 부채꼴의 넓이 차이
(큰 부채꼴)$-$(작은 부채꼴)
$=\dfrac{6\pi}{2}\times 9 -\dfrac{4\pi}{2}\times 6$
$=27\pi-12\pi=15\pi$ - [사다리꼴 변형] $\rightarrow$ 아래 링크 게시글 참고
$\dfrac{1}{2}\times(4\pi+6\pi)\times 3=15\pi$
- 부채꼴의 넓이 차이
- 겉넓이 : $\bbox[#ffff00]{13\pi}+\bbox[#ffc5fd]{15\pi}=28\pi$
$\bigstar$ 옆넓이 $\rightarrow$ 사다리꼴 변형 계산
원뿔대의 옆넓이 쉽게 구하는 방법
원뿔대의 옆넓이를 쉽게 구하는 방법은 부채꼴의 넓이에 대한 설명에 자세히 정리해 두었습니다. 학습을 원하시면 아래의 링크를 이용해 주세요.
구의 겉넓이
구의 겉넓이는 중학교 1학년 수준에서 다루기 어렵습니다. 따라서 실생활에 이용되는 사실을 통해 직관적으로 받아들이기로 합시다.
지도와 구의 겉넓이


지도를 만들 때 사용하는 원통 투사(Cylinerical Projection)를 이용해 구의 겉넓이를 정리해 보자.
그림과 같이 지구표면을 원통에 투사해 원통에 그림자를 만들면 $\bbox[#ffff00]{\text{면적이 유지}}$되는 성질이 있다. 따라서 다음이 성립한다.
- 구의 반지름이 $r$ 일 때
- 원기둥의 반지름 : $r$
- 원기둥의 높이 : $2r$
(구의 겉넓이)$=$(원기둥의 옆넓이)$=2\pi r \times 2r=4\pi r^2$
이상으로 입체도형의 겉넓이에 대한 정리를 마무리 하도록 하겠습니다. 구의 겉넓이에대한 중학교 수준의 증명은 아래의 링크에 자세히 다루었습니다.
