이번 시간과 다음 시간에는 $y=ax^2+bx+c$로 주어진 이차함수 그래프 그리기에 대해 알아보려고 한다. 이번 시간에는 $a,\; b,\; c$의 값이 구체적으로 주어진 이차함수의 그래프를 그리는 방법에 대하여 학습하고, $y=ax^2+bx+c$의 축과 꼭짓점을 바로 구할 수 있는 공식에 대해 알아보기로 하자.
목차
학습목표
- $y=ax^2+bx+c$의 그래프를 인수분해를 이용해 그릴 수 있다.
- $y=ax^2+bx+c$의 그래프를 $y=a(x-p)^2+q$꼴로 변형하여 그릴 수 있다.
- $y=ax^2+bx+c$의 축과 꼭짓점을 구하는 공식을 유도할 수 있다.
이차함수 그래프 그리기
$y=ax^2+bx+c\;\; (a\neq0)$ 의 그래프를 그리는 방법에는 두 가지가 있다.
- $a,\;b,\;c$ 값이 구체적으로 주어진 경우
- $a,\;b,\;c$의 부호만 주어진 경우
이번 시간에는 $a,\;b,\;c$ 값이 구체적으로 주어진 경우에 대해 살펴보자.
학습에 들어가기 전 이전 학년에서 배운 절편에 대한 정의를 정리하고 학습을 이어가도록 하자.
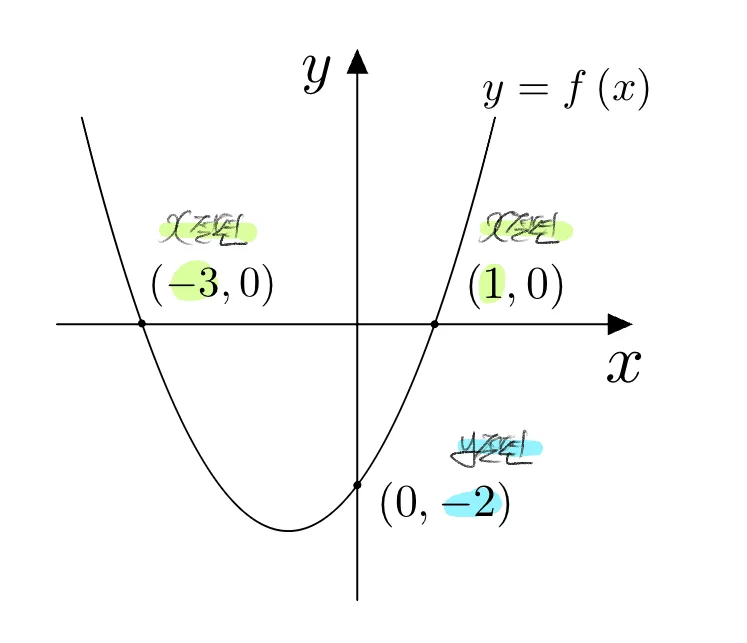
함수 $y=f(x)$의 $x$ 절편, $y$ 절편
- $x$절편 정의 : 함수의 그래프가 $x$축과 만나는 교점의 $x$좌표를 $x$절편 이라고 한다.
이 때 교점의 $y$좌표는 $0$이므로 다음과 같이 정리할 수 도 있다.
$\therefore$ $x$절편 : $y=0$일 때 $x$값 - $y$절편 정의 : 함수의 그래프가 $y$축과 만나는 교점의 $y$좌표를 $y$절편 이라고 한다.
이 때 교점의 $x$좌표는 $0$이므로 다음과 같이 정리할 수 있다.
$\therefore$ $y$절편 : $x=0$일 때 $y$값
a,b,c 값을 이용한 이차함수 그래프
$y=ax^2+bx+c$의 각 항의 계수가 주어진 경우에 다음 두 가지 방법으로 그래프를 그릴 수 있다.
- 인수분해를 이용
- 평행이동식을 이용
인수분해를 이용하는 방법
$y=ax^2+bx+c$로 표현된 이차함수의 이차식 부분인 $ax^2+bx+c$이 인수분해가 가능하면 $x$절편과 이차항계수의 부호를 이용해 쉽게 구할 수 있다. 또한 $x$절편의 값을 이용하면 구체적인 축과 꼭짓점도 구할 수 있다. 다음의 예를 통해 구체적으로 살펴 보기로 하자.
인수분해로 $y=4x^2-4x-3$ 그래프 그리기
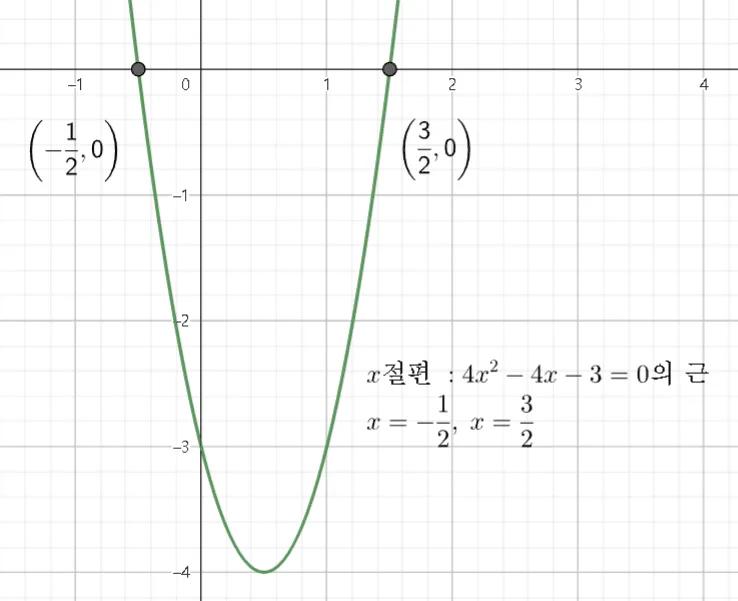
인수분해가 가능한 이차식이 주어진 경우 인수분해와 이차항 계수를 이용해 대략적인 그래프를 그릴 수 있다.
$y=4x^2-4x-3\; \rightarrow\; y=(2x+1)(2x-3)$
$x$절편
$y=0$일 때 $x=-\dfrac{1}{2}$ 또는 $x=\dfrac{3}{2}$ 이며
$x$축 과 교점 : $(-\dfrac{1}{2},0)$, $(\dfrac{3}{2},0)$ 이다.
$y=4x^2-4x-3$는 아래로 볼록이다.
($\because\; a=4$)
다음으로 절편을 이용하여 축과 꼭짓점을 구하는 방법에 대해 알아보자.
절편을 이용해 축과 꼭짓점 구하기
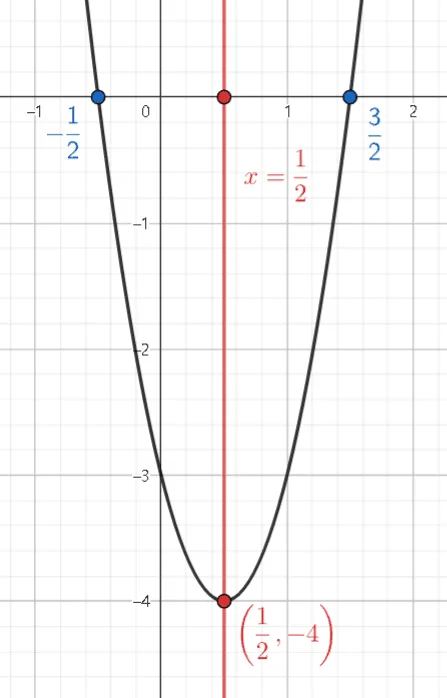
위의 과정을 통해 얻은 $x$절편의 값과 이차함수의 대칭성을 이용하면 축과 꼭짓점을 다음과 같이 구할 수 있다.
축 : $x$절편 사이의 중점을 지난다.
$x=\dfrac{-\dfrac{1}{2}+\dfrac{3}{2}}{2}=\dfrac{1}{2} $
꼭짓점 : $x=\dfrac{1}{2}$일 때 $y=-4$이고
따라서 꼭짓점의 좌표는 $(\dfrac{1}{2},-4)$ 이다.
평행이동으로 $y=4x^2-4x-3$의 그래프 그리기
값이 구체적으로 주어진 $y=ax^2+bx+c$의 그래프를 그리는 두 번째 방법은 함수식을 $y=a(x-p)^2+q$꼴로 변형하여 평행이동을 이용하는 것이다.
주어진 함수를 $y=a(x-p)^2+q$꼴로 변형하여 그래프를 그리는 과정을 다음 두 단계로 나누어 살펴보기로 하자.
- (완전제곱식) $+$ (상수) 꼴로 변형
- 그래프 그리기
- 평행이동을 이용한 그래프 그리기
- 축과 꼭짓점을 이용한 그래프 그리기
$4x^2-4x-3\; \rightarrow\;$ 완전제곱식, 상수
$4x^2-4x-3$는 다음과 같은 과정을 따르면 완전제곱식과 상수 꼴로 변형 할 수 있다. 이는 완전제곱식의 필요 충분조건에 대한 내용이 기초가 된다. 기억이 나지 않는 학생은 다음 링크를 통해 학습하길 바란다. (완전제곱식의 필요충분 조건)
$$\begin{align} &4x^2-4x-3
\\&=4(x^2-x)-3\tag{가}
\\&=4\{x^2-x+\left(-\dfrac{1}{2}\right)^2\}-3-4\times\left(-\dfrac{1}{2}\right)^2\tag{나}
\\&=4\left(x-\dfrac{1}{2}\right)^2-4 \tag{다}&&
\\&\end{align}$$
완전제곱식과 상수로 변형하는 위의 과정을 항등식 변형과정을 단계별로 살펴보자.
(가) 문자와 상수항을 분리, 최고차계수로 분배
(나) 항등식의 성질을 이용한 완전제곱식 구성
(다) 완전제곱식, 상수로 정리
그래프 그리기
$y=4\left(x-\dfrac{1}{2}\right)^2-4$을 이용해 그래프를 그리는 방법에 대해 정리해 보자.
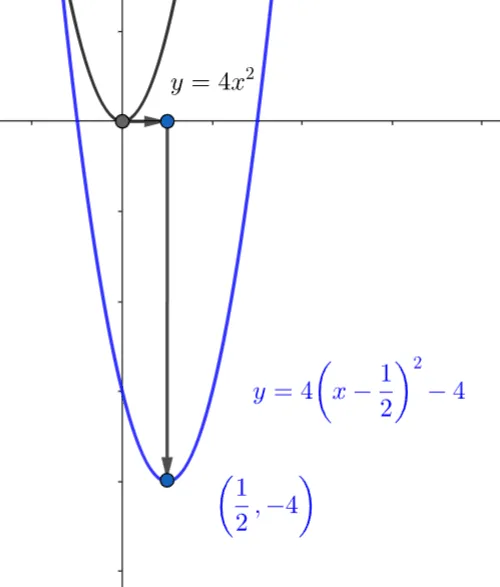
방법1 : 평행이동 이용
$y=4\left(x-\dfrac{1}{2}\right)^2-4$은
$y=4x^2$의 그래프를
$x$축 $\dfrac{1}{2}\;,\;y$축 $-4$만큼 평행이동한 그래프
방법2 : 축과 꼭짓점 이용
$y=4\left(x-\dfrac{1}{2}\right)^2-4$은
축의 방정식이 $x=\dfrac{1}{2}$이고,
꼭짓점의 좌표가 $\left(\dfrac{1}{2},-4\right)$ 인 그래프
평행이동을 이용한 그래프를 그리는 과정은 평행이동 전 그래프를 함께 고려해야 한다.
따라서 일반적으로 방법2의 축과 꼭짓점을 이용한 그래프 그리는 방법을 더 많이 사용한다.
이제부터 축과 꼭짓점을 이용해 더 정확한 그래프를 그리는 방법에 대해 알아보기로 하자.
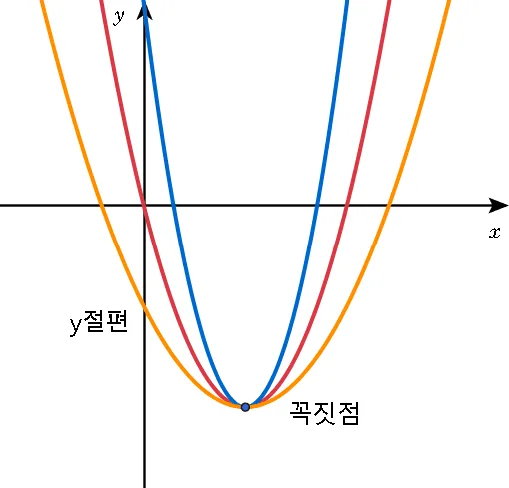
$y=4\left(x-\dfrac{1}{2}\right)^2-4$의 축의 방정식과 꼭짓점은 다음과 같다.
축의 방정식 : $x=\dfrac{1}{2}$
꼭짓점의 좌표 : $\left(\dfrac{1}{2},-4\right)$
이를 이용해 그릴 수 있는 그래프는 $y$ 절편의 부호에 따라 세 가지를 생각 할 수 있다. 다시 말해, $y$절편이 양수, 0 , 음수일 때 각 각 파란색, 빨간색, 노란색 그래프를 생각할 수 있다.
따라서 더 정확한 그래프를 그리기 위해 $y$절편을 구해 보자.
- $y$절편 : $x=0$일 때 함숫값
$y=4\left(x-\dfrac{1}{2}\right)^2-4$ 또는 $y=4x^2-4x-3$ 식을 이용 가능
두 식중 $y=4x^2-4x-3$을 이용하는 것이 편리하다. - $y$절편 : $y=4x^2-4x-3$의 상수항 $-3$
이를 종합하면 노란색 그래프가 $y=4x^2-4x-3$의 그래프 임을 알 수 있다.
마지막으로 $y=ax^2+bx+c$이 주어질 때 축과 꼭짓점의 좌표를구할 수 있는 공식에 대해 알아보고 마무리 하도록 하자.
$y=ax^2+bx+c$의 축, 꼭짓점 공식유도
$y=ax^2+bx+c$의 축과 꼭짓점을 구하는 식을 유도하는 과정도 완전제곱식과 상수로 표현하는 과정이 필요하다.
$y=ax^2+bx+c\;\rightarrow\;y=a(x-p)^2+q$
위의 문제를 통해 $y=ax^2+bx+c$로 주어진 이차함수를 평행이동 식을 $y=a(x-p)^2+q$으로 변형하면 축과 꼭짓점을 구할 수 있음을 알 수 있다.
$ax^2+bx+c\;\rightarrow\;$완전제곱식 + 상수 꼴로 정리
$$\begin{align}&ax^2+bx+c
\\&=a\left( x^2+\dfrac{b}{a}x\right)+c\tag{가}
\\&=a \left\{x^2+\dfrac{b}{a}x+\left( \dfrac{b}{2a}\right)^2\right\}+c-a\times\dfrac{b^2}{4a^2}\tag{나}
\\&=a \left(x+ \dfrac{b}{2a}\right)^2-\dfrac{b^2-4ac}{4a}\tag{다}
\\& \end{align}$$
$y=ax^2+bx+c$의 축과 꼭짓점
$y=ax^2+bx+c$의 축과 꼭짓점은 변형식 $y=a \left(x+ \dfrac{b}{2a}\right)^2-\dfrac{b^2-4ac}{4a}$의 축과 꼭짓점과 같다. 따라서 다음과 같이 정리 할 수 있다.
- 축의 방정식 : $x=-\dfrac{b}{2a}$
- 꼭짓점의 좌표 : $\left(-\dfrac{b}{2a}, -\dfrac{b^2-4ac}{4a}\right)$
정리
$y=ax^2+bx+c$ 그래프 그리는 방법
- 인수분해 가능할 때
x절편을 이용 - 인수분해 불가능할 때
$y=a(x-p)^2+q$꼴로 변형하여 평행이동/ 축, 꼭짓점 이용
$y=ax^2+bx+c$의 축과 꼭짓점
- 축의 방정식 : $x=-\dfrac{b}{2a}$
- 꼭짓점의 좌표 : $\left(-\dfrac{b}{2a}, -\dfrac{b^2-4ac}{4a}\right)$
