이번 시간에는 이차식 인수분해를 쉽게 하는 방법에 대해 학습해 보기로 하자. 이해를 돕기 위해 결론부터 이야기하고 원리에 대해 설명을 이어가도록 하겠다.
목차
이차식 인수분해
이차식은 간단히 인수분해 될 수도 있으나 간단한 일차식(정수계수 일차식)으로 인수분해가 어려운 경우도 있다. 먼저 이를 빠르게 파악하는 것이 인수분해를 잘하는 핵심이다.
만약 간단히 인수분해를 못한다면 근의 공식을 써야 하기 때문이다.
인수분해 가능성 빠르게 판단하기
이차항과 상수항의 부호는 같을 수도 있고 다를 수도 있다. 각 경우에 대한 인수분해 요령은 다음과 같다.
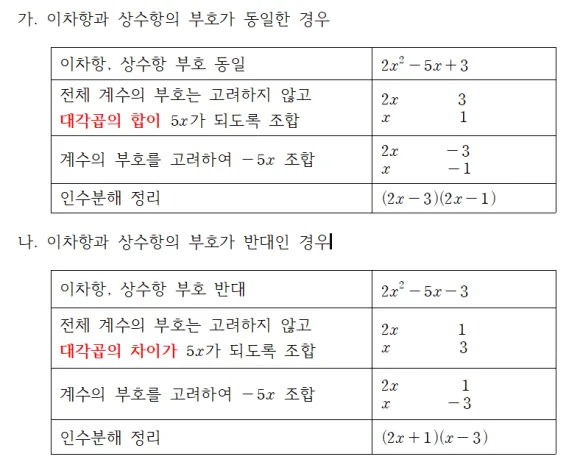
만약 이차항과 상수항의 부호가 같다면 (가)의 논리를 이용하고, 다르다면 (나)의 논리를 사용하면 쉽게 이차식을 인수분해 할 수 있다.
정리
이차항과 상수항의 부호를 비교하여
부호가 같으면
$\rightarrow$대각합으로 일차계수 절댓값 맞추기
$\rightarrow$ 일차항을 고려한 부호결정
부호가 다르면
$\rightarrow$대각차로 일차계수 절댓값 맞추기
$\rightarrow$ 일차항을 고려한 부호결정
이차식 인수분해 논리 적용
[문제1] $3x^2+11x+6$
[풀이]
이차항($3x^2$)과 상수항(6)의 부호가 같으므로 대각합으로 11x를 맞추면 다음과 같이 인수분해가 된다.
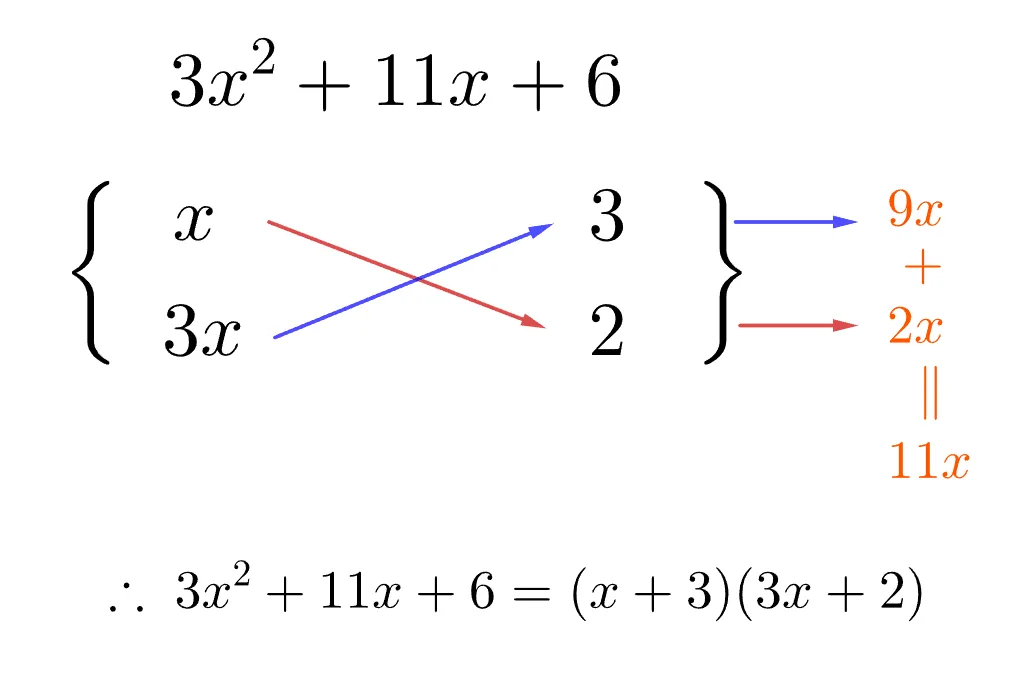
양쪽의 부호는 그대로 두고 일차항의 부호가 반대이면 어떻게 되는지 확인해 보자.
[문제2] $3x^2-11x+6$
[풀이]
이차항($3x^2$)과 상수항(6)의 부호가 같다. 따라서 부호는 생각하지 말고 대각합으로 11x를 먼저 맞추기로 하자.
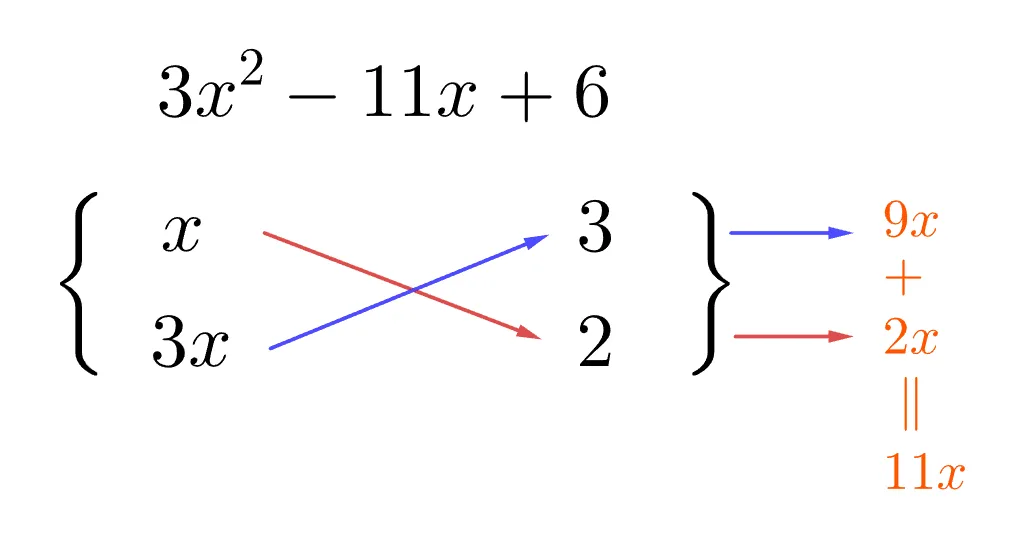
이제 일차항의 계수 $-11x$를 맞추기 위해 아래와 같이 부호를 결정하면 인수분해가 마무리 된다.
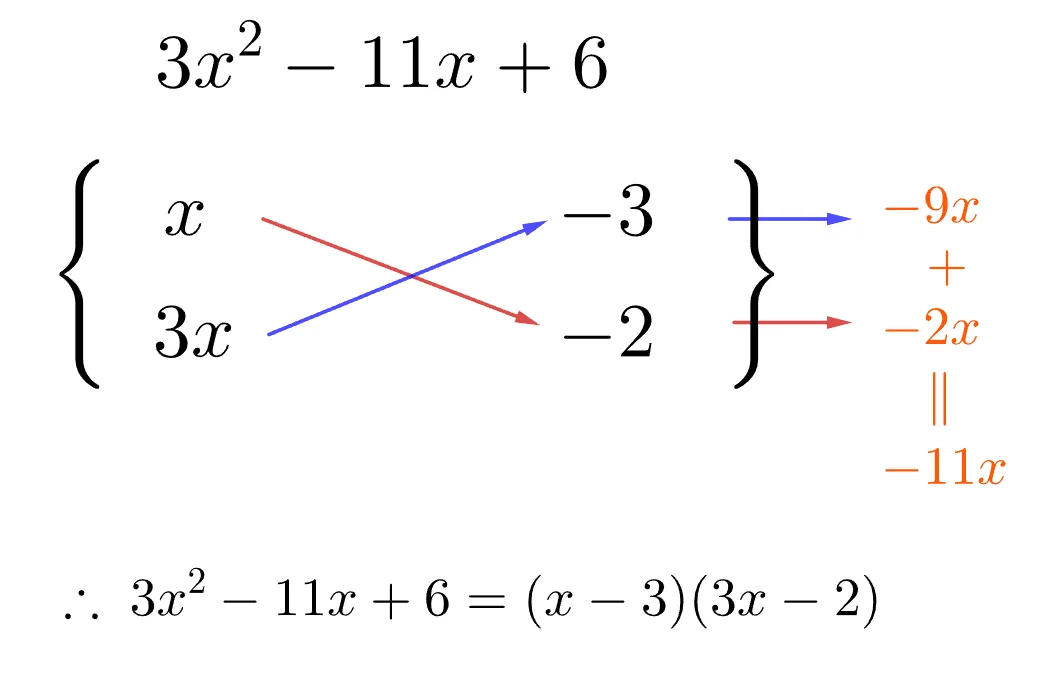
[문제3] $6x^2-xy-2y^2$
[풀이]
x에 대한 이차항 ($6x^2$) 과 상수항 (-2y^2)은 부호가 다르다. 따라서 대각곱의 차이를 xy로 만드는 값의 조합을 찾으면 다음과 같은 조합을 찾을 수 있다.
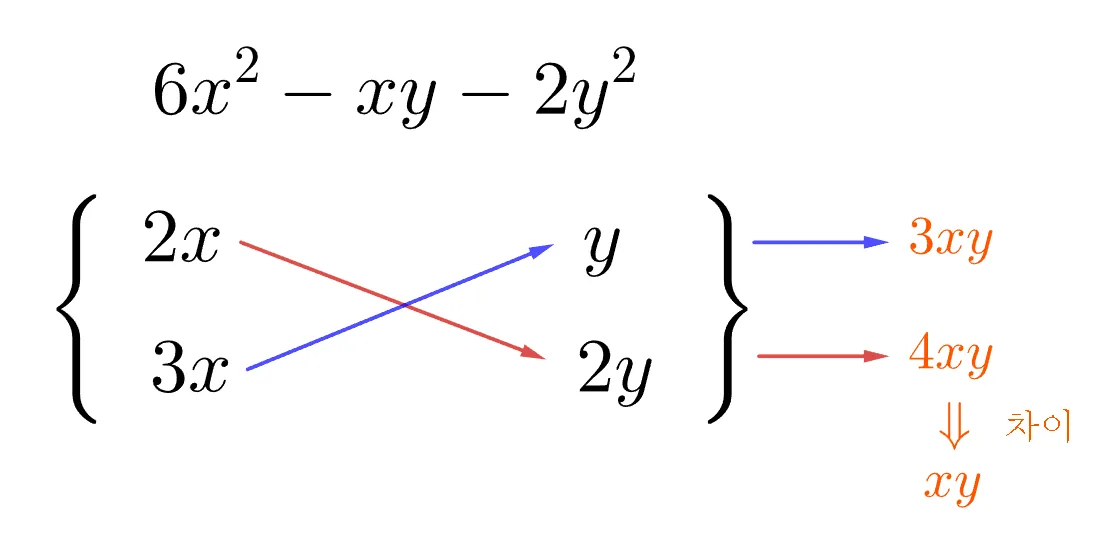
여기서 $3xy-4xy=-xy$ 를 만족할 수 있도록 부호를 결정하면 다음과 같이 인수분해가 됨을 알 수 있다.
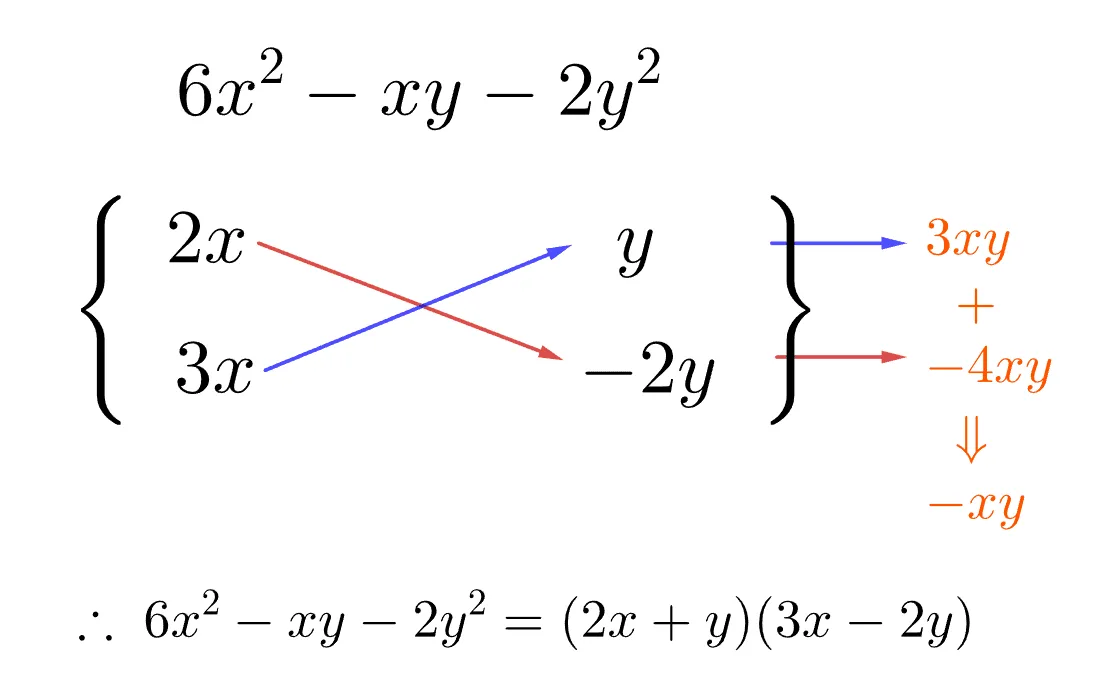
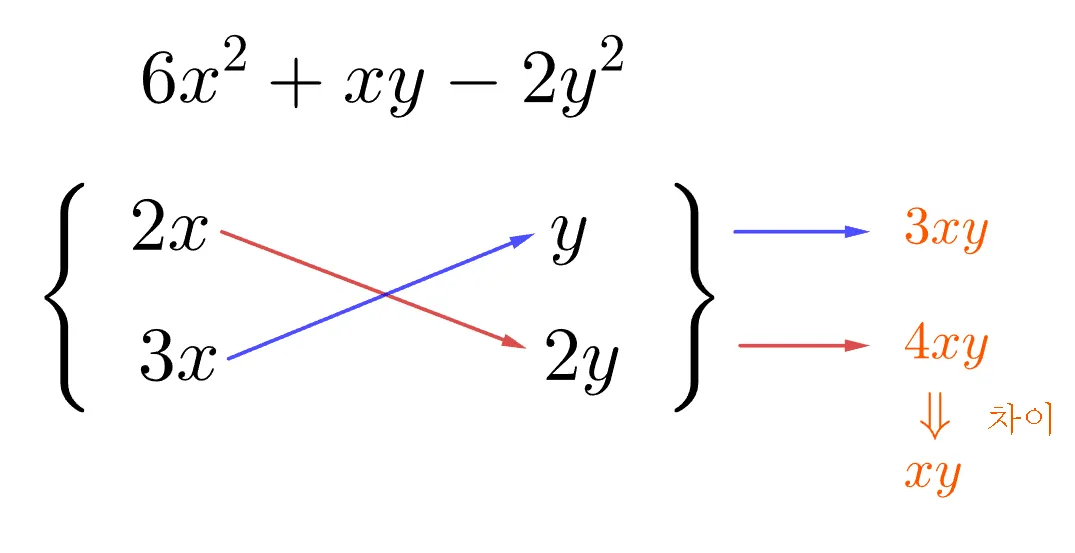
[문제4] $6x^2+xy-2y^2$
[풀이]
이 문제도 3번과 동일하게 x에 대한 이차항 ($6x^2$) 과 상수항 (-2y^2)은 부호가 다르므로 대각곱의 차이가 $xy$가 되는 조합을 동일하게 찾을 수 있다.
이 다음 과정은 $4xy-3xy=xy$를 맞추어 일차항을 맞춰주면 인수분해를 마무리 할 수 있다.
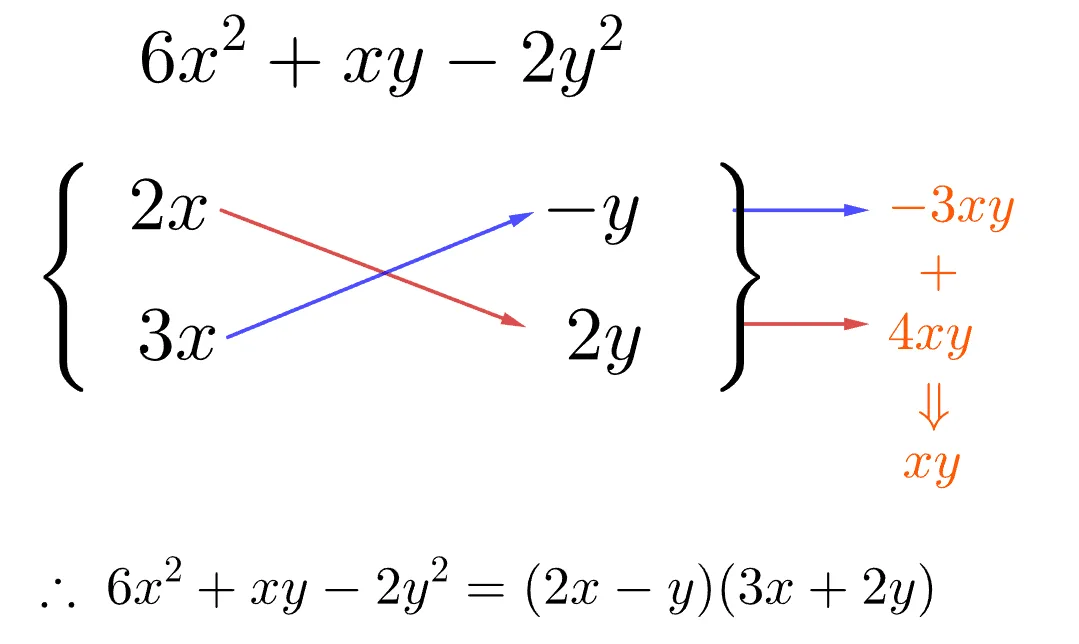
정리
이차식의 인수분해에 대해 다시 한 번 정리하고 학습을 마무리 하자.
이차항과 상수항의 부호를 비교하여
- 부호가 같으면
$\rightarrow$대각합으로 일차항 절댓값 맞추기
$\rightarrow$ 일차항 부호결정 - 부호가 다르면
$\rightarrow$대각차로 일차항 절댓값 맞추기
$\rightarrow$ 일차항 부호결정
