원주각의 개념은 단순하지만 원주각 활용과 관련된 문제는 쉽지 않다. 이번 시간에는 활용 문제에 자주 등장하고, 수학적으로 의미 있는 유형을 정리하여 활용문제에 대한 자신감을 끌어 올려보자.
목차
학습목표
- 원주각의 활용을 유형별로 정리하여 다양한 상황에 응용할 수 있도록 한다.
원주각 기본이론 복습
원 위의 점에 대해 아래와 같은 성질이 항상 성립한다.
- 동일한 호에대한 원주각의 크기가 같다.
- 원에 내접하는 사각형의 한 외각은 내대각의 크기와 같다.
- 접선과 현이 이루는 각은 내부의 호에 대한 원주각과 같다.
이를 토대로 원주각의 문제 유형에 대하여 살펴보자.
복습 링크
원주각에 대한 복습이 필요한 학생은 다음의 링크를 활용하길 바란다.
한 원에서 원주각의 활용 유형

유형1
- $\overparen{CD}$의 원주각 : $\angle{DAC}=\angle{DBC}=a$
- $\overparen{AB}$의 원주각 : $\angle{DAC}=\angle{DBC}=b$
- 삼각형의 닮음 : $\triangle{EAD}\sm\triangle{EBC}$
- 내부 점 $E$ 에서 방멱의 정리 : $ac=bd$
유형2
- $\overparen{AD}$의 원주각 : $\angle{ABD}=\angle{ACD}=c$
- $\overparen{BC}$의 원주각 : $\angle{BAC}=\angle{BDC}=d$
- 삼각형의 닮음 : $\triangle{EAB}\sm\triangle{EDC}$
- 내부 점 $E$ 에서 방멱의 정리 : $ac=bd$


유형3
유형1, 유형2 의 성질을 모두 만족하고 추가로 다음을 만족한다.
- 원에 내접 하는 $\square{ABCD}$ : $x+y+z+w=180^{\circ}$
- 내대각 : $\angle{FAB}=\angle{BCD}=y+w$, $\angle{FBA}=\angle{CDA}=y+z$
- $\triangle{ABC}$에서 $\angle{FBA}=y+z$
$\triangle{ABD}$에서 $\angle{FAB}=y+w$ - $\triangle{FBD}$에서 $\angle{DFB}=x-y$
- 삼각형의 닮음 : $\triangle{FAB}\sm\triangle{FCD}$
- 외부의 점 $F$에서 방멱의 정리 : $ad=bc$
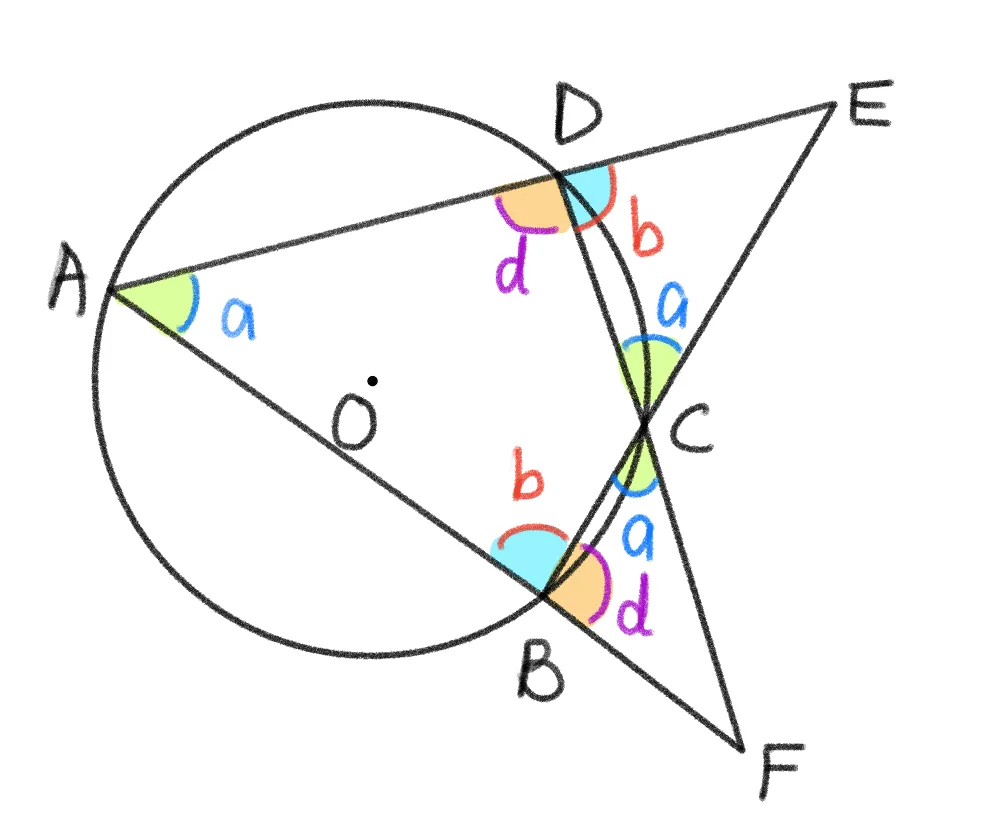
유형4
- 내대각 : $\angle{DAB}=\angle{DCE}=\angle{DAB}=a$ $\angle{ABC}=\angle{CDE}$=b
$\angle{ADC}=\angle{CBF}=d$ - 삼각형의 닮음 : $\triangle{EAB}\sm\triangle{ECD}$ , $\triangle{FAD}\sm\triangle{FCB}$
- 외부의 점 $F$에서 방멱의 정리 : $\overline{ED}\times\overline{EA}=\overline{EC}\times\overline{EB}$
- 외부의 점 $E$에서 방멱의 정리 : $\overline{FB}\times\overline{FA}=\overline{FC}\times\overline{FD}$
한 원에서 원주각을 활용하는 유형에 대하여 살펴보았다 다음으로 두 원에서 원주각을 활용하는 유형에 대해 살펴보자.
두 원에서 원주각의 활용 유형
두 원이 만나면 원주각을 활용하여 다음과 같은 사실을 알 수 있다.
두 원이 한 점에서 만날 때

유형1. $\overline{AB}//\overline{CD}$
- 접현각: $\angle{ABQ}=\angle{AQP}=\angle{CQR}=\angle{QDC}$
- $\angle{ABQ}=\angle{QDC}$ $\;$ $\therefore\overline{AB}//\overline{CD}$
- 추가 정리
$\angle{BAQ}=\angle{BQR}=\angle{PQD}=\angle{QCD}$
닮음 : $\triangle{QAB}\sm\triangle{QCD}$
유형2. $\overline{AB}//\overline{CD}$
- 접현각: $\angle{DQR}=\angle{QCD}=\angle{QAB}$
- $\angle{QCD}=\angle{QAB}$ $\;$ $\therefore\overline{AB}//\overline{CD}$
- 추가 정리
$\angle{CQP}=\angle{CDQ}=\angle{ABQ}$
닮음 : $\triangle{QAB}\sm\triangle{QCD}$

두 원이 두 점에서 만날 때

유형1. $\overline{AB}//\overline{EF}$
- 내대각 : $\angle{BAD}=\angle{DCE}=\angle{DFG}$
- $\angle{BAD}=\angle{DFG}$ $\;$ $\therefore \overline{AB}//\overline{EF}$
- 추가 정리
$\angle{BCD}=\angle{DFE}$
유형2. $\overline{AB}//\overline{EG}$
- 내대각 : $\;$ $\angle{BAD}=\angle{DCF}$
- 접현각: $\angle{DCF}=\angle{DFG}$
- $\angle{BAD}=\angle{DFG}$ $\;$ $\overline{AB}//\overline{EG}$
- 추가 정리
$\angle{ABC}=\angle{CDF}=\angle{CFE}$
$\triangle{FCD}\sm\triangle{FAB}$
원 밖의 한 점 $P$에서 방멱 정리


유형3. $\overline{AB}//\overline{EF}$
- 내대각 : $\angle{BAD}=\angle{DCG}$
- $\overparen{DF}$의 원주각: $\angle{DCG}=\angle{DEF}$
- $\angle{BAG}=\angle{GEF}$ $\;$ $\therefore\overline{AB}//\overline{EF}$
- 추가 정리
$\angle{ABC}=\angle{CDG}=\angle{GEF}$
$\triangle{GAB}\sm\triangle{GCD}\sm\triangle{GEF}$
원 밖의 한 점$G$에서 방멱의 정리
심화유형

심화유형1
두 원의 교점 $B,D$와 할선 $\overline{AE},\overline{AC}, \overline{DG}, \overline{CG}$이 다음과 같을 때 $\overline{AE}//\overline{CG}$이 성립한다.
- $\overparen{BE}$의 원주각: $\angle{BAE}=\angle{BDE}$
- $\overparen{BG}$의 원주각: $\angle{BDG}=\angle{BCG}$
- $\overline{AD}//\overline{FC}$ ($\because\angle{BAE}=\angle{BCG}$)
심화유형2
두 원의 교점 $B,D$와 할선 $\overline{AD}, \overline{BD}\overline{AC}$ 작은 원의 접선 $\overline{DF}$가 다음과 같을 때$\overline{AD}//\overline{FC}$이 성립한다.
- 접현각: $\angle{DAB}=\angle{BDF}$
- $\overparen{BF}$의 원주각: $\angle{BDF}=\angle{BCF}$
- $\angle{DAB}=\angle{BCF}$ $\therefore\overline{AD}//\overline{FC}$

정리
원주각의 뜻은 단순하지만, 원주상의 어떤 점에서도 생각할 수 있기에 활용의 범위가 매우 넓다. 여기서는 자주 등장하는 유형만 다루고 있다. 유형마다 숨겨진 원리를 이해한다면 더 복잡한 문제도 잘 해결할 수 있을 것이라 확신한다.
