이번 시간에는 원주각과 중심각 사이의 관계를 증명하는 과정에 대해 정리해 보기로 하자. 중학교 과정에서 증명은 모든 경우에 대한 증명을 다루고 있지 않는다. 여기서는 모든 경우를 고려하여 수학적으로 좀 더 완벽한 증명을 제시하려고 한다.
목차
학습목표
- $(중심각\;)=\dfrac{1}{2}\times (원주각\;)$ 임을 수학적으로 설명할 수 있다.
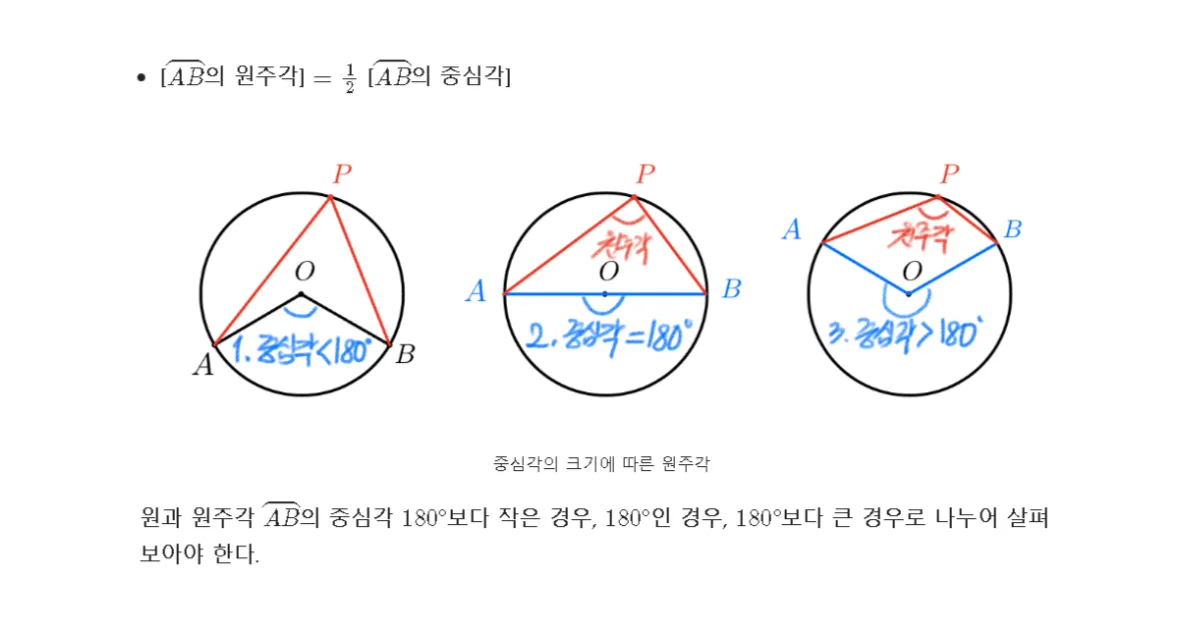
호에 대한 원주각은 중심각의 $\frac{1}{2}$임을 보이는 과정을 논리적으로 빠짐없이 서술하려고 한다. 일반적으로 호의 중심각이 $180^{\circ}$를 넘지 않는 범위에서 증명을 마무리하는 경우가 많은데 중심각이 $180^{\circ}$인 경우와 $180^{\circ}$보다 큰 경우까지 다루어야 완벽한 증명이라 할 수 있다.
원주각의 뜻
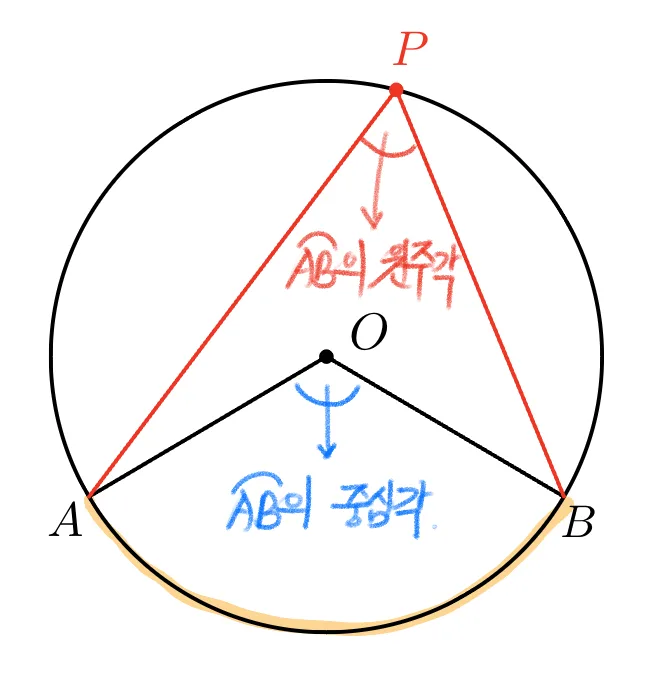
원 $O$와 $\overparen{AB}$위에 있지 않는 점 $P$에 대하여
- 호에 대한 중심각 : 중심에서 호의 양 끝을 바라보는 반직선 사이의 각도
- 호에 대한 원주각 : 주어진 호를 제외한 원주 위에 있는 점에서 호의 양 끝을 바라보는 반직선 사이의 각도
- 예시
$\angle{APB}$ : $\overparen{AB}$의 원주각
$\angle{APB}$ : $\overparen{AB}$의 중심각

원주각과 중심각 사이의 관계
이제 본격적으로 동일한 호에 대한 원주각과 중심각 사이에 다음 관계가 성립한다.
- [$\overparen{AB}$의 원주각] $=$ $\frac{1}{2}$ [$\overparen{AB}$의 중심각]
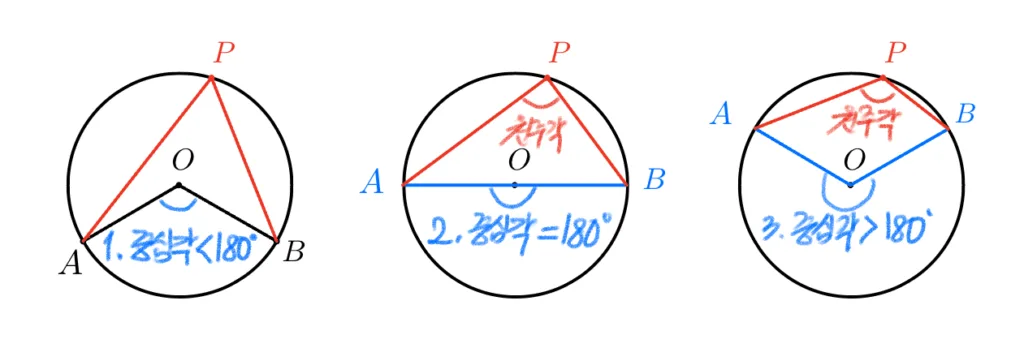
원과 원주각 $\overparen{AB}$의 중심각 $180^{\circ}$보다 작은 경우, $180^{\circ}$인 경우, $180^{\circ}$보다 큰 경우로 나누어 살펴보아야 한다.
증명
[$\overparen{AB}$ 의 중심각]$\,<180^{\circ}$
$\overparen{AB}$의 중심각 크기가 180도 보다 작은 경우에 원주각은 다양한 모양으로 나타나기 때문에 다음과 같은 경우로 나누어 증명 한다.
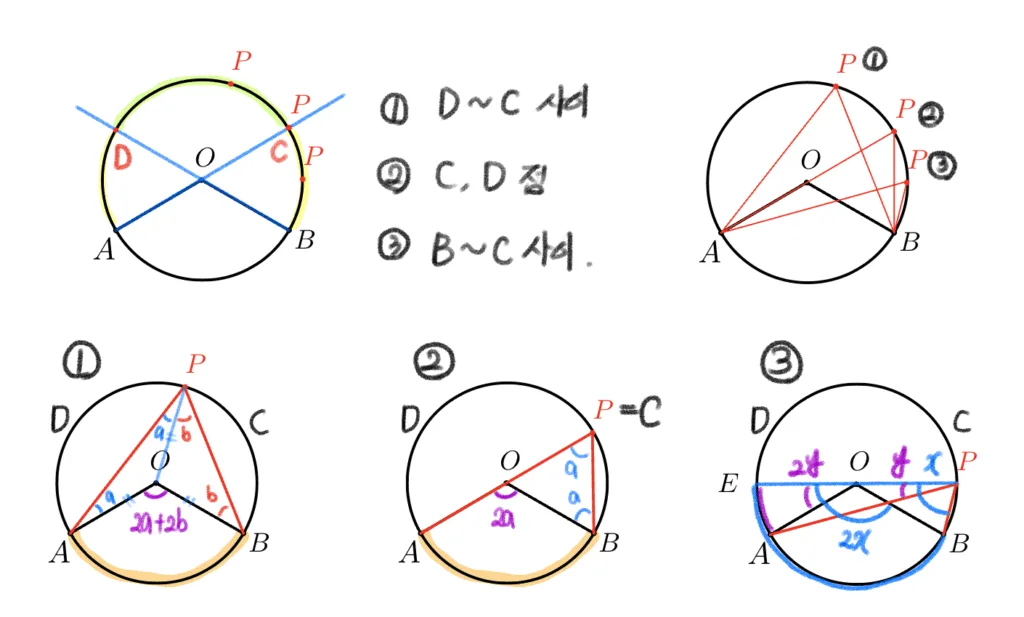
Case1
- $\triangle{OAP},\triangle{OBP}$ 이등변삼각형 : $\angle{OAP}=\angle{OPA}=a\;,\;\angle{OBP}=\angle{OPB}=b$
- $\angle{APB}=a+b$, $\angle{AOB}=2a+2b$
- $\therefore$ [$\overparen{AB}$의 중심각]$=2\times$[$\overparen{AB}$의 원주각]
이 과정은 중학교 2학년 외심의 각에 대한 성질을 보이는 과정과 동일하다.
case2
- $\triangle{OBP}$ 이등변 삼각형 : $\angle{OPB}=\angle{OBP}=a$ , $\angle{AOB}=2a$
- $\therefore$ [$\overparen{AB}$의 중심각]$=2\times$[$\overparen{AB}$의 원주각]
case3
- case2 적용 : $\angle{EPB}=x$ 이면 $\angle{EOB}=2x$
- case2 적용 : $\angle{EPA}=y$ 이면 $\angle{EOA}=2y$
- 두식의 차 : $\angle{APB}=x-y$ , $\angle{AOB}=2x-2y$
- $\therefore$ [$\overparen{AB}$의 중심각]$=2\times$[$\overparen{AB}$의 원주각]
이제 중심각의 크기가 180도 이상인 경우에 대한 원주각과 중심각 사이 관계에 대해 증명을 이어가 보자.
[$\overparen{AB}$ 의 중심각]$\,\geq 180^{\circ}$
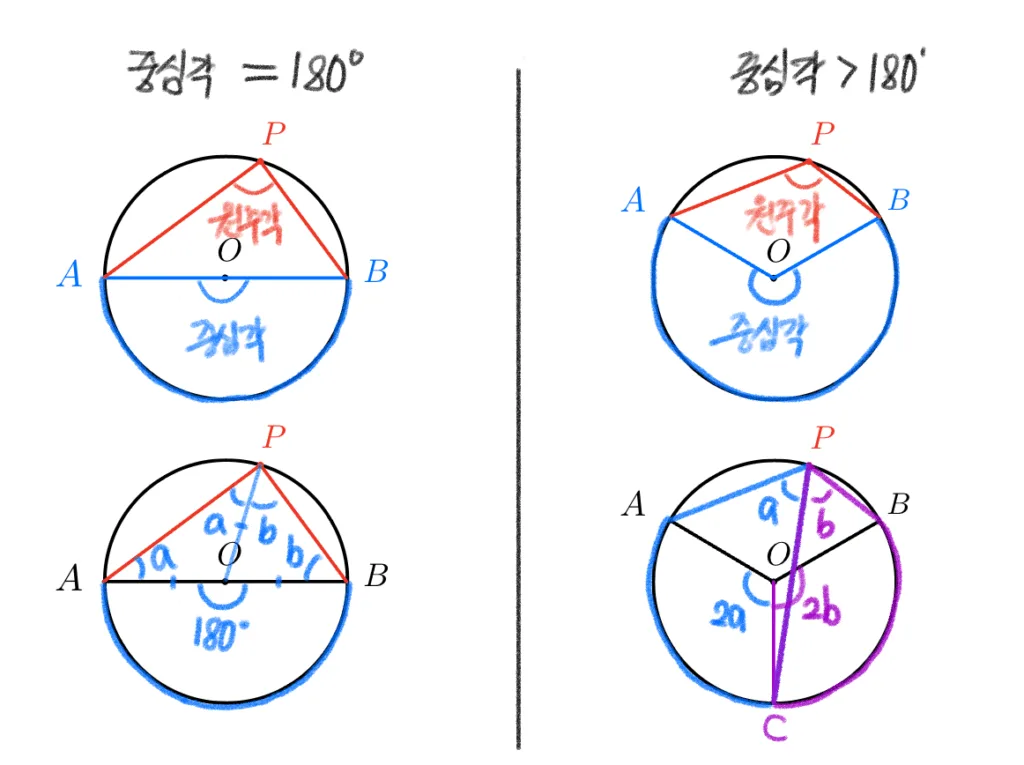
[$\overparen{AB}$ 의 중심각] $=180^{\circ}$ 인 경우
- $\overline{OA}=\overline{OB}=\overline{OP}$
- $\angle{OPA}=\angle{OAP}$ , $\angle{OPB}=\angle{OBP}$
- $\triangle{APB}$ : $2a+2b=180^{\circ}$ , $\therefore a+b=90^{\circ}$
[$\overparen{AB}$ 의 중심각] $<180^{\circ}$ 인 경우
$A,B$로 분할되는 긴 호의 중점 $C$에 대하여
- [$\overparen{AC}$ 의 중심각]$\,<180^{\circ}$ case1 : $\angle{AOC}=2\times\angle{APC}=2a$
- [$\overparen{CB}$ 의 중심각]$\,<180^{\circ}$ case3 : $\angle{BOC}=2\times\angle{BPC}=2b$
- 두 식의 합 : [$\overparen{AB}$ 의 중심각]$=2a+2b$
- $\therefore$[$\overparen{AB}$ 의 중심각]$=2\times[\overparen{AB}$의 원주각]
정리
위와 같은 과정을 통해 우리는 [$\overparen{AB}$의 원주각] $=$ $\frac{1}{2}$ [$\overparen{AB}$의 중심각] 임을 알수 있다. 이를 다른 관점에서 정리하면 원위의 한 점에서 두 반직선을 그을 때 그 각도가 같으면 반직선 으로 잘린 호의 길이가 같다는 것이다. 마지막으로 다음을 정리하고 마무리 하자.
- 원주각이 같으면 중심각이 같고 호의 길이도 같으며 부채꼴의 넓이도 같다.