직사각형, 마름모, 정사각형은 중학교 수학에서 자주 등장하는 기본 도형이지만, 정의와 성질, 그리고 이들 사이의 관계를 완벽히 구분해 기억하는 것은 생각보다 쉽지 않습니다. 특히 ‘평행사변형이 직사각형·마름모·정사각형이 되는 조건’은 단순한 암기가 아니라, 증명 과정을 통해 논리적 사고력을 기를 수 있는 좋은 주제입니다.
이번 글에서는 여러가지 사각형의 성질, 조건을 증명을 통해 체계적으로 정리하고, 각 조건이 왜 성립하는지를 단계별로 살펴보려고 합니다. 글을 끝까지 이해하려고 노력하면 도형 간의 관계와 증명의 흐름이 머릿속에 자연스럽게 자리 잡아 수학적 사고력이 한층 탄탄해질 것입니다.
목차
직사각형
직사각형은 네 각이 모두 직각인 사각형으로, 평행사변형의 성질을 그대로 가지면서도 대각선의 길이가 같다는 특징을 추가로 갖습니다. 직사각형의 정의에서 부터 성질, 그리고 평행사변형이 직사각형이 되는 조건까지 논리적으로 정리해 봅시다.
직사각형의 정의는 다음과 같고 아래와 같은 이유로 평행사변형이 됩니다.
- 직사각형 정의: 네 각의 크기가 모두 같은 사각형(네 각의 크기가 $90^\circ$)
- 직사각형은 두 쌍의 대각의 크기가 같으므로 평행사변형이다. (평행사변형의 조건)
직사각형의 대각선 성질
- 직사각형의 두 대각선은 길이가 같고, 서로 다른 것을 이등분한다.
직사각형은 평행사변형이므로 대각선이 서로 다른 것을 이등분합니다. 따라서 보여야 할 것은 대각선의 길이가 같다는 사실입니다. (평행사변형의 성질 복습)
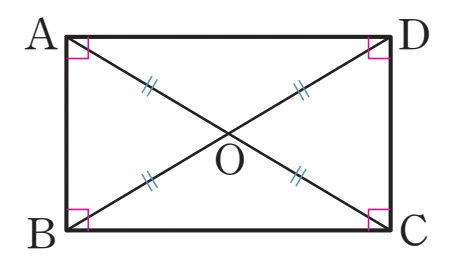
[증명]
직사각형 $\square{ABCD}$에 대하여 $\square{ABCD}$는 평행사변형이고, 다음이 성립합니다.
$\triangle{ABC} \equiv \triangle{DCB}$ (SAS 합동)
- $\overline{AB}=\overline{CD}$, $\overline{BC}$(공통), $\angle{ABC}=\angle{DCB}$
따라서 $\therefore \overline{AC}=\overline{DB}$입니다.
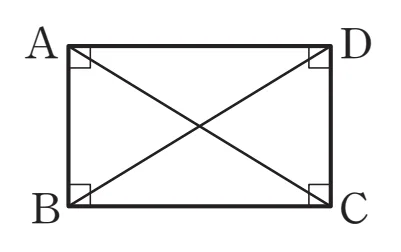
대각선의 길이가 같고 서로 이등분하므로 다음이 성립합니다.
- $\overline{OA}=\overline{OB}=\overline{OC}=\overline{OD}$
평행사변형이 직사각형이 되는 조건
평행사변형이 다음 중 어느 한 조건을 만족 시키면 직사각형이 됩니다.
- 한 내각이 직각이다.
- $\angle {A}=90^\circ$인 평행사변형 $\square{ABCD}$은 직사각형이다.
- 두 대각선의 길이가 같다. (대각선 조건)
- $\overline{AC}=\overline{BD}$인 평행사변형 $\square{ABCD}$은 직사각형이다.
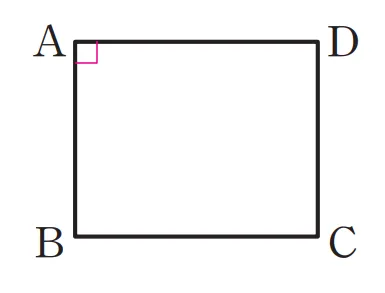
[조건1 증명]
$\angle {A}=90^\circ$인 평행사변형 $\square{ABCD}$는 다음을 만족합니다.
평행사변형의 성질: 두 쌍의 대각의 크기가 각각 같고, 이웃하는 각의 크기 합이 $180^\circ$
따라서 $\angle {A}=90^\circ$이면 $\angle {A}=\angle {B} = \angle {C}=\angle {D}=90^\circ$이고, $\square{ABCD}$ 는 직사각형입니다.
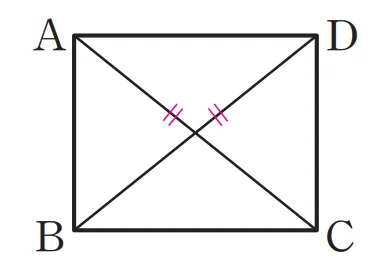
[조건2 증명]
$\overline{AC}=\overline{BD}$인 평행사변형 $\square{ABCD}$은 다음을 만족합니다.
$\overline{AC}=\overline{BD}$(평행사변형의 성질)이고, 대각선의 길이가 같고, $\overline{BC}$가 공통이므로 $\triangle{ABC} \equiv \triangle{DCB}$ (SSS 합동)입니다.
따라서 $\angle{B}=\angle{C}$이고 이웃 하는 내각의 크기의 합이 $180^\circ$(평행사변형의 성질)이므로 한 내각의 크기가 $90^\circ$입니다.
한 내각의 크기가 $90^\circ$인 평행사변형이므로 직사각형이 됩니다. (조건1)
마름모
이제 마름모의 정의와 성질, 조건에 대해 정리해 보도록 합시다. 마름모의 정의는 아래와 같고 정의에 의해 평행사변형이 됨을 알 수 있습니다.
- 마름모: 네 변의 길이가 모두 같은 사각형
- 두 쌍의 대변의 길이가 각각 같으므로 마름모는 평행사변형입니다.
마름모의 대각선 성질
- 마름모의 두 대각선은 서로 다른 것을 수직이등분한다.
- 마름모의 두 대각선에 의해 생기는 4개의 삼각형은 모두 합동이다.
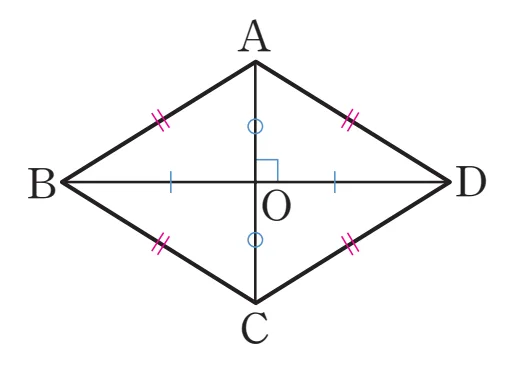
[성질1, 2 증명]
마름모의 두 대각선 $\overline{AC},\ \overline{BD}$의 교점 $O$에 대하여 다음이 성립합니다.
- $\triangle AOB \equiv \triangle AOD$ (SSS 합동)
- $\overline{AB}=\overline{AD}$ (마름모의 정의)
- $\overline{AO}$는 공통
- $\overline{OB}=\overline{OD}$ (평행사변형의 성질)
- $\triangle{AOB} \equiv \triangle{COB} \equiv \triangle{COD} \equiv \triangle{AOD}$ (SSS 합동)
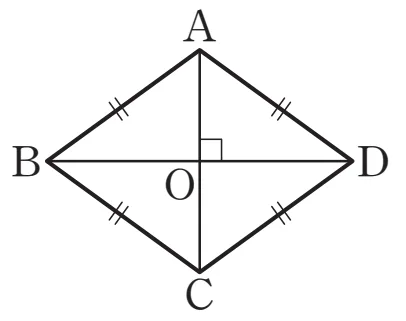
따라서 대응각 $\angle{AOB} = \angle {AOD}=90^\circ$이고, $\overline{AC} \perp \overline{BD}$입니다. 결과적으로 $\overline{AC},\ \overline{BD}$는 서로 수직 이등분함을 알 수 있습니다.
평행사변형이 마름모가 되는 조건
평행사변형이 다음 조건을 만족하면 마름모가 됩니다.
- 이웃하는 두 변의 길이가 같다.
- $\overline{AB}=\overline{BC}$인 평행사변형 $\square{ABCD}$가 마름모이다.
- 두 대각선이 서로 수직이다. (대각선 조건)
- $\overline{AC} \perp \overline{BD}$인 평행사변형 $\square{ABCD}$가 마름모이다.
[조건1 증명]
평행사변형은 대변의 길이가 같고, 이웃하는 두 변의 길이가 같다는 조건이 추가되면, 네 변의 길이가 같게 됩니다. 따라서 마름모가 됩니다.
[조건2 증명]
평행사변형은 두 대각선이 서로를 이등분하고, $\overline{AC} \perp \overline{BD}$를 만족하면 다음이 성립합니다.
- $\triangle{AOB}$와 $\triangle{AOD}$ (SAS 합동)

비슷한 방법으로 $\triangle{AOB} \equiv \triangle{COB} \equiv \triangle{COD} \equiv \triangle{AOD}$ (SAS 합동)이고 따라서 네 변의 길이가 같고 $\square{ABCD}$는 마름모가 됩니다.
정사각형의 정의 성질 조건
정사각형의 성질과 조건에 대한 증명은 위에서 증명한 사실을 토대로 증명할 수 있습니다. 정의 부터 차근차근 정리하면서 어떤 논리를 사용하고 있는지 확실히 이해하시길 바랍니다.
- 정사각형: 네 변의 길이가 모두 같고, 네 내각의 크기가 모두 같은 사각형
- 정사각형은 마름모이면서 직사각형.
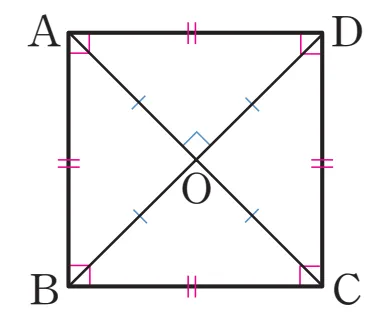
정사각형의 대각선 성질
정사각의 대각선에 대한 성질은 다음과 같습니다.
- 정사각형의 두 대각선은 길이가 같고, 서로를 수직 이등분한다.
$\overline{AC} = \overline{BD}$, $\overline{AC} \perp \overline{BD}$, $\overline{AO} = \overline{BO} = \overline{CO} = \overline{DO}$
[증명]
정사각형은 직사각형이면서 마름모 이므로 다음 성질을 만족합니다.
- 직사각형의 대각선 성질: 두 대각선의 길이가 같고 서로를 이등분 한다.
- 마름모의 대각선 성질: 두 대각선이 서로를 수직이등분 한다.
정사각형이 되는 조건
직사각형이 정사각형이 되는 조건
직사각형이 정사각형이 되려면 마름모의 정의 와 대각선의 성질까지 만족해야 합니다. 따라서 평행사변형이 마름모가 될 조건을 추가하면 됩니다.
- 이웃하는 두 변의 길이가 같다.
- 두 대각선이 서로 수직이다.
마름모가 정사각형이 되는 조건
마름모가 다음 중 어느 한 조건을 만족시키면 정사각형이 됩니다.
- 한 내각이 직각이다.
- 두 대각선의 길이가 같다.
여러가지 사각형의 정의 성질 조건 정리
| 도형 | 정의 | 대각선 성질 |
|---|---|---|
| 평행사변형 | 두 쌍의 대변 평행 | 이등분 |
| 직사각형 | 네 각의 크기 | 길이가 같고 이등분 |
| 마름모 | 네 변의 길이 | 수직 이등분 |
| 정사각형 | 네 변의 길이 네 각의 크기 | 길이가 같고 수직 이등분 |
| 도형 | 조건 $\Rightarrow$ | 도형 |
|---|---|---|
| 평행사변형 | 한 내각이 직각이다. 두 대각선의 길이 같다 | 직사각형 |
| 평행사변형 | 이웃한 두 변의 길이 같다. 두 대각선이 서로 수직 | 마름모 |
| 직사각형 | 이웃한 두 변의 길이가 같다 두 대각선이 서로 수직 | 정사각형 |
| 마름모 | 한 내각이 직각이다. 두 대각선의 길이가 같다. | 정사각형 |
위의 내용을 토대로 아래와 같이 도식화 하여 정리할 수 있습니다.
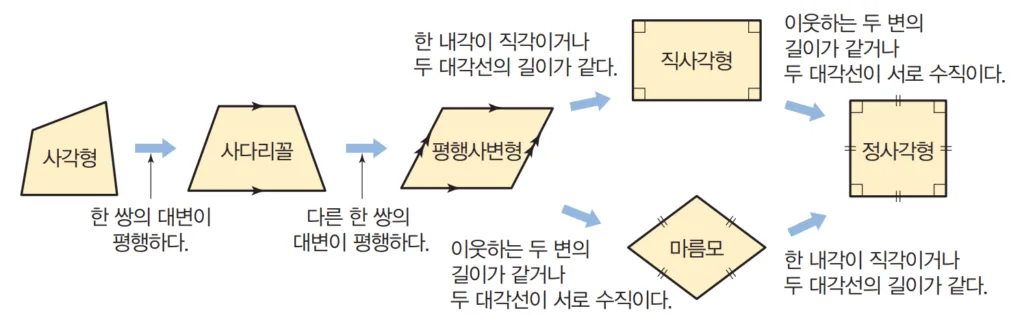
[이미지 출처: 개념원리]
