삼각형의 내각과 외각을 이등분하는 각의 이등분선은 대변의 길이를 일정한 비(두 변의 길이비)로 나눕니다. 이번 글에서는 이등분선이 만들어내는 비례 관계를 평행선과 선분의 길이의 비를 이용해 증명하는 과정을 정리해 보았습니다. 삼각형의 각의 이등분선을 내분점과 외분점으로 생각하면 각의 이등분선을 보는 관점이 완전히 달라질 것입니다. 끝까지 읽고 정리해 보세요!
목차
삼각형의 각의 이등분선 성질
삼각형의 각의 이등분선은 다음과 같은 성질을 가지고 있습니다.
- 삼각형의 내각의 이등분선은 대변을 두 변의 길이 비로 내분
- 삼각형의 외각의 이등분선은 대변의 연장선을 두 변의 길이 비로 외분합니다.
이 성질에 대한 증명에 대해 정리해 봅시다.
삼각형의 내각의 이등분선
삼각형의 내각의 이등분선은 $\color{red}\text{양 쪽 두 변의 길이 비}$로 $\color{blue}\text{대변을 내분}$하는 성질을 증명하는 과정에 대해 정리해 봅시다.
$\triangle ABC$에서 $\angle A$의 이등분선이 $\overline{BC}$와 만나는 점을 D라 하면
- ${\color{red}\overline{AB} : \overline{AC}} ={\color{blue} \overline{BD} : \overline{CD}}$
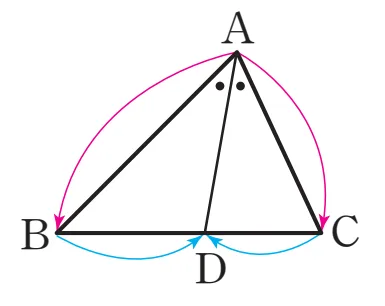
증명1
$\triangle ABC$에서 $\angle A$의 이등분선이 $\overline{BC}$와 만나는 점을 D에 대하여
오른쪽 그림과 같이 점 C를 지나고 $\overline{AD}$에 평행한 직선과 $\overline{BA}$의 연장선과의 교점을 E라 하면
$\angle BAD = \angle AEC$ (동위각), $\angle DAC = \angle ACE$ (엇각)이므로 $\angle AEC = \angle ACE$입니다.
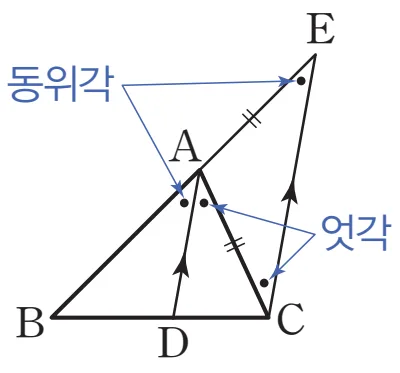
$\overline{AC} \bbox[#ffff00]{=} \overline{AE} \cdots \text{㉠}$ ($\triangle ACE$ 이등변 삼각형)
$\overline{BA} : \bbox[#ffff00]{\overline{AE}} = \overline{BD} : \overline{DC} \cdots \text{㉡}$ (평행선과 선분의 길이의 비)
$\therefore \ \overline{AB} :\bbox[#ffff00]{\overline{AC}} = \overline{BD} : \overline{CD}$ (㉠, ㉡)
따라서 삼각형의 내각의 이등분선은 $\color{red}\text{양 쪽 두 변의 길이 비}$로 $\color{blue}\text{대변을 내분}$합니다.
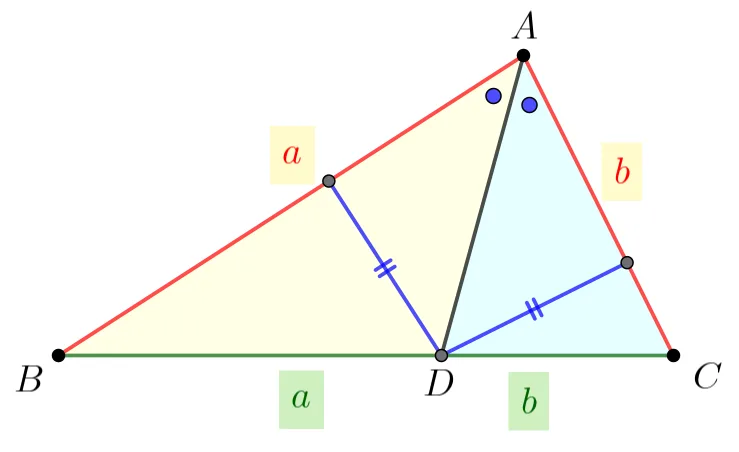
증명2
$\triangle ABC$에서 $\angle A$의 이등분선이 $\overline{BC}$와 만나는 점을 D라 하고, $\overline{AB}:\overline{AC}=a:b$ 일 때
$\triangle ABD : \triangle ADC=a:b$ 이므로
$\overline{BD} : \overline{DC}=a:b$이다.
삼각형의 외각의 이등분선
삼각형의 외각의 이등분선은 $\color{red}\text{양쪽 두 변의 길이의 비}$로 $\color{blue}\text{대변을 외분}$하는 성질에 대해 정리해 봅시다.
$\triangle ABC$에서 $\angle A$의 외각의 이등분선이 $\overline{BC}$의 연장선과 만나는 점을 D라 하면
${\color{red}\overline{AB} : \overline{AC}} = {\color{blue}\overline{BD} : \overline{CD}}$
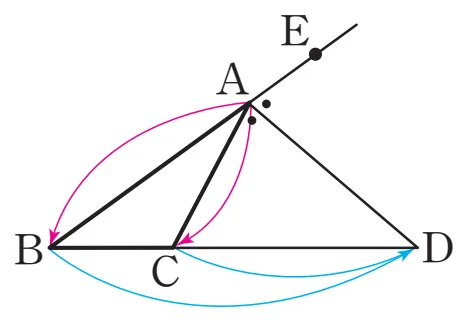
증명
$\triangle ABC$에서 $\angle A$의 외각의 이등분선이 $\overline{BC}$의 연장선과 만나는 점을 D에 대하여, 오른쪽 그림과 같이 점 C를 지나고 $\overline{AD}$에 평행한 직선을 그어 $\overline{AB}$와의 교점을 F라 하면,
$\angle EAD = \angle AFC$ (동위각), $\angle DAC = \angle ACF$ (엇각)이므로 $\angle AFC = \angle ACF$ 입니다.
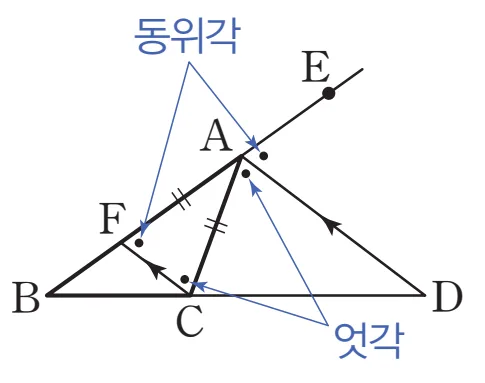
$\overline{AF} \bbox[#ffff00]{=} \overline{AC} \cdots \text{㉠}$ ($\triangle AFC$ 이등변 삼각형)
$\overline{AB} : \bbox[#ffff00]{\overline{AF}} = \overline{DB} : \overline{DC} \cdots \text{㉡}$ (평행선과 선분의 길이의 비)
$\therefore \ \overline{AB} : \bbox[#ffff00]{\overline{AC}} = \overline{BD} : \overline{CD}$ (㉠, ㉡)
따라서 삼각형의 외각의 이등분선은 $\color{red}\text{양쪽 두 변의 길이의 비}$로 $\color{blue}\text{대변을 외분}$함을 알 수 있습니다.
정리: 삼각형의 각의 이등분선
삼각형의 각의 이등분선의 성질은 다음과 같이 간단히 정리할 수 있습니다.
- 내각의 이등분선 : $\color{red}\text{양쪽 두 변의 길이의 비}$로 $\color{blue}\text{대변을 내분}$한다.
- 외각의 이등분선 : $\color{red}\text{양쪽 두 변의 길이의 비}$로 $\color{blue}\text{대변을 외분}$한다.
[출처: 개념원리]
