평행선의 동위각 엇각에 대한 성질 기하를 체계적으로 학습하는데 핵심이 되는 요소입니다. 이번 시간에는 이 성질들이 어떻게 성립할 수 있는지 증명을 통해 다루고 두 직선이 평행할 조건에 대한 증명까지 다루었습니다.
목차
동위각 엇각
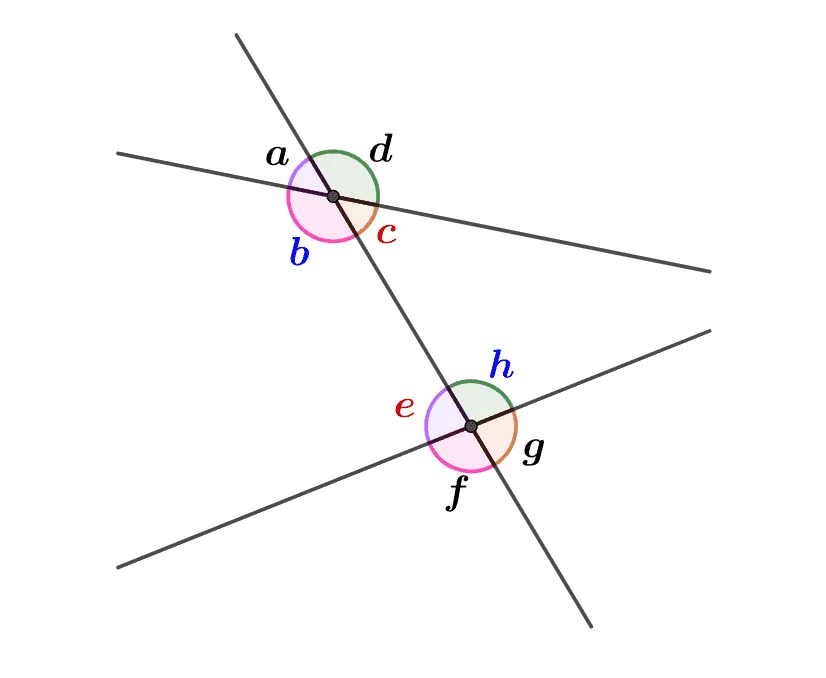
한 평면 위의 세 직선 $l,\;m,\;n$로 만들어진 교점이 2개 이상일 때
- 동위각 : 서로 같은 위치에 있는 두 각
- $(\bbox[#f4ebfe]{\angle{a},\angle{e}})$, $(\bbox[#fee6f4]{\angle{b},\angle{f}})$, $(\bbox[#fbeee6]{\angle{c},\angle{g}})$, $(\bbox[#e6f0e7]{\angle{d},\angle{h}})$
- 엇각 : 서로 엇갈린 위치에 있는 두 각
- $({\color{#0000ff}\angle{b},\angle{h}})$, $({\color{#dc143c}\angle{c},\angle{e}})$
주어진 그림에서 동위각은 4쌍, 엇각은 2쌍이다.
엇각과 동위각 사이의 관계
두 직선 $l,\;m$이 한 직선 $n$과 만날 때
- 엇각의 크기가 같으면 동위각의 크기가 같다.
- 동위각의 크기가 같으면 엇각의 크기가 같다.
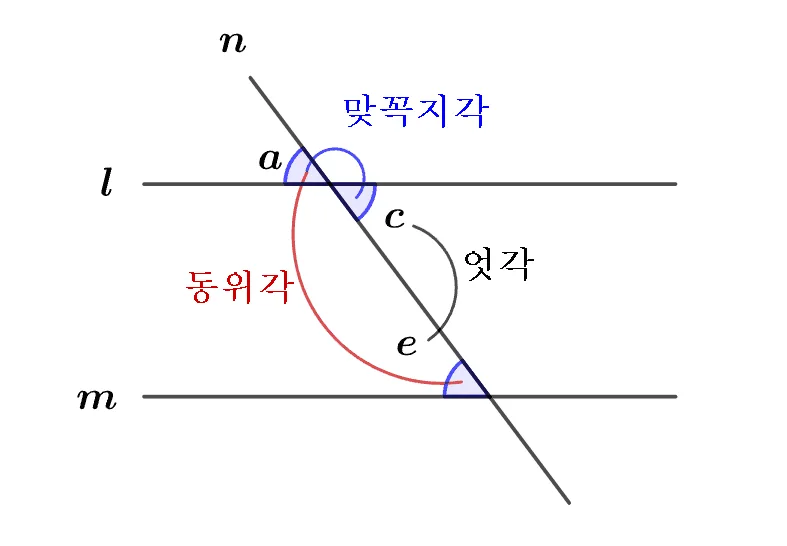
[증명]
- 엇각이 같으면 동위각도 같다.
- $e\overset{\underset{\text{엇각}}{}}{=}c$ 이면 $e=c\overset{\underset{\text{맞꼭지각}}{}}{=}a$
$\therefore\; a=e$(동위각이 같다)
- $e\overset{\underset{\text{엇각}}{}}{=}c$ 이면 $e=c\overset{\underset{\text{맞꼭지각}}{}}{=}a$
- 동위각이 같으면 엇각도 같다.
- $e\overset{\underset{\text{동위각}}{}}{=}a$ 이면 $e=a\overset{\underset{\text{맞꼭지각}}{}}{=}c$
$\therefore\; e=c$(엇각이 같다)
- $e\overset{\underset{\text{동위각}}{}}{=}a$ 이면 $e=a\overset{\underset{\text{맞꼭지각}}{}}{=}c$
위의 사실로 부터 동위각 4쌍과 엇각 2쌍이 같음을 보이는 것은 한쌍의 동위각 또는 엇각에 대해 같음을 보이는 것으로 충분함을 알 수 있다.
평행선의 성질 증명
평행한 두 직선 $l,\;m$과 한 점에서 만나는 직선$n$에 대하여 다음이 성립한다.
- $a+b=180^\circ$ (아래 그림)
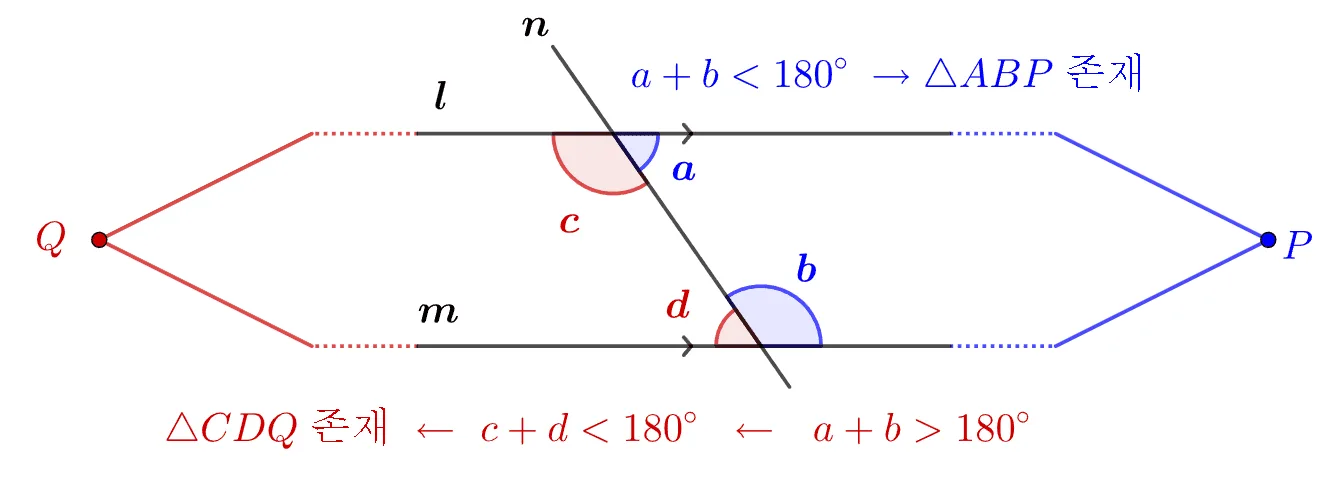
위의 사실을 직접 보이는 것은 쉽지 않다. 따라서 다음과 같은 논리를 이용하기로 하자.
- $a+b\neq180^\circ$이면 말이 안된다.
- 따라서 $a+b=180^\circ$이다.
[증명]$a+b\neq180^\circ$이면 말이 안됨을 보이자.
$a+b\neq180^\circ$인 경우는 다음과 같은 두 가지 상황 뿐이다.
- $a+b<180^\circ$이면
- $\rightarrow \triangle{ABP}$가 만들어진다.
- $a+b>180^\circ$이면
- $\rightarrow c+d<180^\circ$$\rightarrow \triangle{CDQ}$가 만들어진다.
위의 사실은 $l\pam$이라는 사실과 모순된다. 따라서 $a+b=180^\circ$이다.
Q.E.D.
평행선의 동위각 엇각 성질 증명
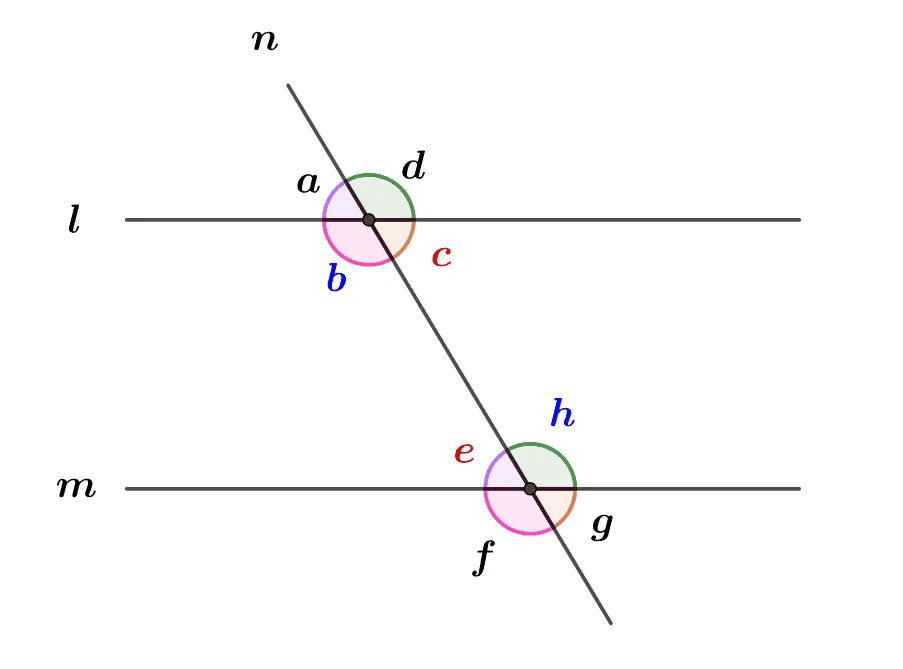
평행한 두 직선 $l,\;m$이 한 직선 $n$과 만날 때
- 동위각의 크기가 같다.
- $(\bbox[#f4ebfe]{\angle{a}=\angle{e}})$, $(\bbox[#fee6f4]{\angle{b}=\angle{f}})$, $(\bbox[#fbeee6]{\angle{c}=\angle{g}})$, $(\bbox[#e6f0e7]{\angle{d}=\angle{h}})$
- 엇각의 크기가 같다.
- $({\color{#0000ff}\angle{b}=\angle{h}})$, $({\color{#dc143c}\angle{c}=\angle{e}})$
[증명]
동위각과 엇각의 기본 성질에 의해 한 쌍의 엇각이 같음을 보이면 충분하다.
- $e+h=180^\circ$ (평각)
- $c+h=180^\circ$ ($l\pam$)
- $e=c$ (엇각이 같다)
Q.E.D.
두 직선이 평행할 조건
서로 다른 두 직선 $l,\;m$이 한 직선과 서로 다른 두 점에서 각 각 만날 때
- 한 쌍의 동위각이 같으면 $\rightarrow\;l\pam$
- 한 쌍의 엇각이 같으면 $\rightarrow\;l\pam$
동위각 조건 증명
한 쌍의 동위각이 같으면 두 직선이 평행함을 다음과 같은 논리로 보이자.
- 한 쌍의 동위각이 같을 때 두 직선이 평행하지 않는다면 말이 안된다. 따라서 평행하다.
[증명]
$\angle{a}=\angle{e}$일 때 $l\pam$임을 보이는 것이 쉽지 않다. 따라서 여기서도 $l,\;m$이 평행하지 않는다면 말이 안됨을 보이기로 하자.
$\angle{a}=\angle{e}=\angle{c}$이고 $l,\;m$이 평행하지 않는다면 한 점에서 만나고 다음과 같은 경우로 나누어 생각할 수 있다.
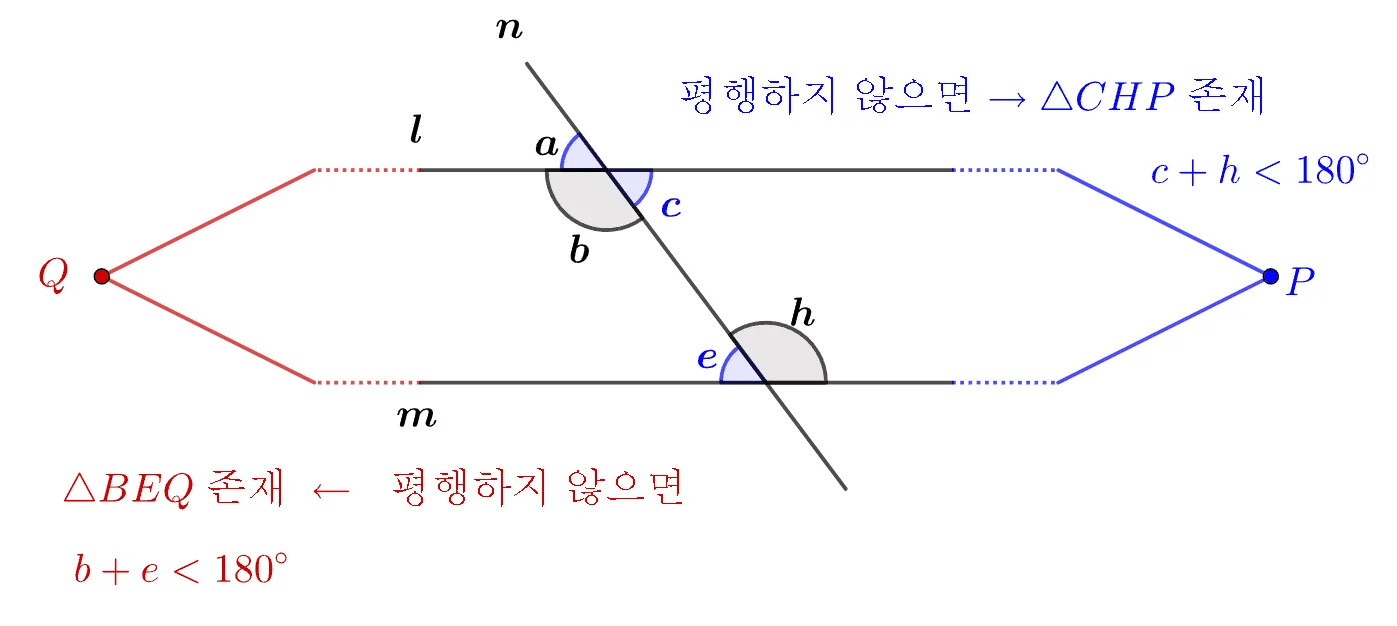
- $l,\;m$이 오른쪽에서 만나는 경우 : 교점 $P$
- $\triangle{CHP}$가 존재
- $c+h<180^\circ,\;e+h=180^\circ$
- $\angle{e}=\angle{c}$이므로 말이 안된다.
- $l,\;m$이 왼쪽에서 만나는 경우 : 교점 $Q$
- 비슷한 방법으로 보일 수 있다.
따라서 $l\pam$일 수 밖에 없다.
QED.
엇각 조건 증명
서로 다른 두 직선 $l,\;m$이 한 직선과 서로 다른 두 점에서 각 각 만날 때 다음의 사실을 보이자.
- 엇각이 같으면 $\rightarrow\;l\pam$
[증명]
$\bbox[#ffff00]{\text{엇각과 동위각 사이의 관계}}$와 $\bbox[#dcff8c]{\text{동위각이 같으면 두 직선이 평행하다}}$는 사실을 이용하면 다음과 같이 증명할 수 있다.
- 엇각이 같다$\xrightarrow[]{\quad}$ 동위각이 같다.$\xrightarrow[]{\quad}$ 두 직선이 평행하다.
따라서 엇각이 같으면 두 직선이 평행하다.
QED.
맺음말
평행선의 동위각과 엇각에 대한 성질은 앞으로 배울 기하학을 정리하는데 매우 중요한 개념입니다. 하지만 이 개념을 논리적으로 증명하는 것은 중학교 학생들에게 있어 쉽지 만은 않은 과정이지만, 이 과정을 극복하지 않고 수학적 사고력을 높일 수 없습니다. 수학을 수학답게 학습하길 바랍니다.
