동위각 엇각 문제 유형 정리 심화 실생활

동위각과 엇각의 성질은 평행선을 이용한 문제에 핵심적인 개념입니다. 다양한 문제해결 능력을 기르기 위해 위해 대표적인 동위각 엇각 문제 유형을 정리하고 심화문제와 실생활 적용문제를 풀어보려고 합니다.

동위각 엇각 문제 유형 정리

유형1

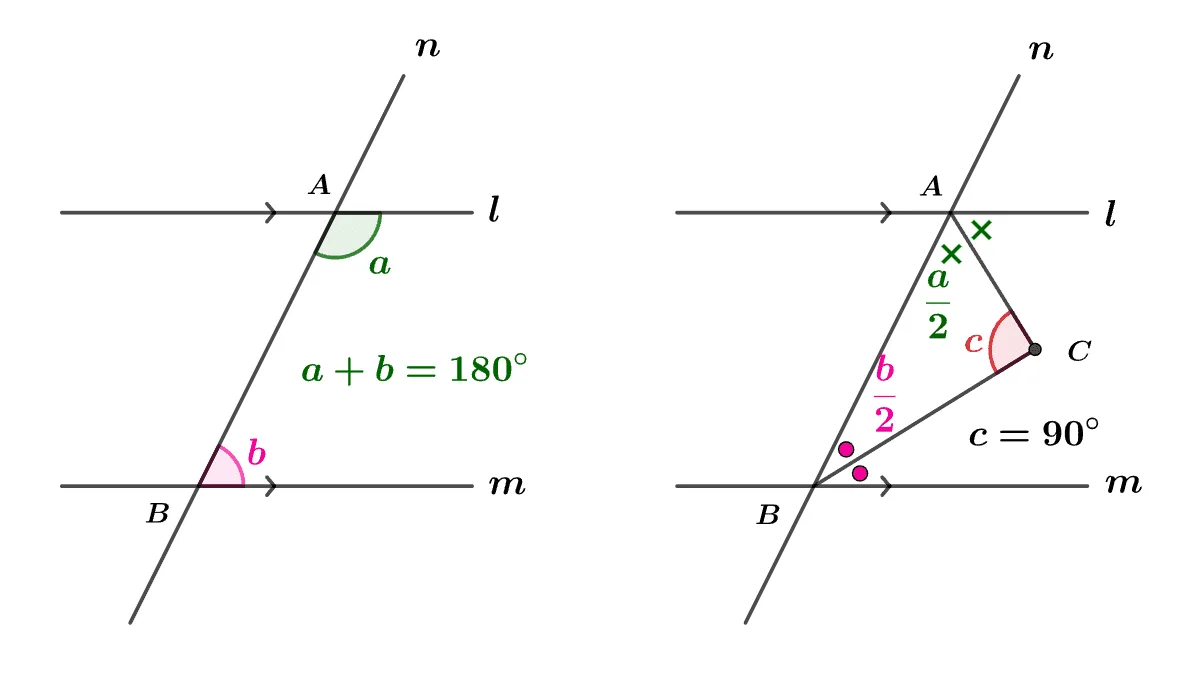
평행한 두 직선 $l,\;m$과 직선 $n$이 한점에서 만날 때 주어진 $\angle{a},\; \angle{b}$와 두 각의 이등분 선의 교점 $C$에 대하여 다음이 성립한다.

• $a+b=180 ^\circ$
  • 평행선의 성질
• $\angle{c}=90^\circ$
  • $\dfrac{a}{2}+\dfrac{b}{2}+c=180^\circ$이고 $\dfrac{a}{2}+\dfrac{b}{2}=90^\circ$이기 때문

유형2

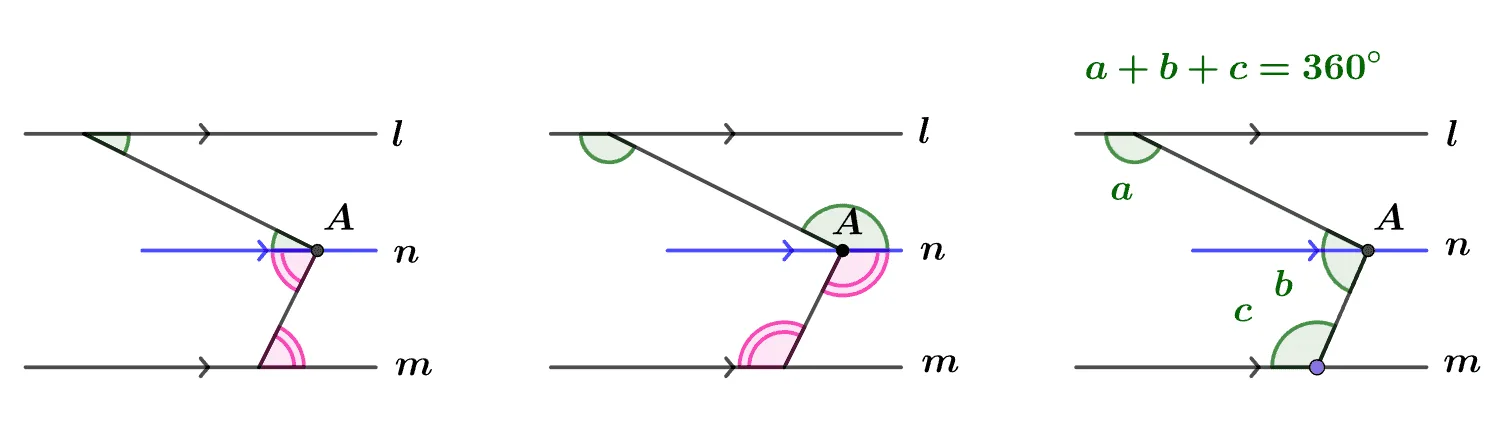
평행한 직선 $l,\;m$에 대하여 다음이 성립한다.

• $A$를 지나고 $l,\;m$에 평행한 직선 $n$을 그릴 수 있다.
• 엇각의 성질을 이용하여 $\angle{A}$의 크기를 구할 수 있다.
• 유형1을 적용하면 $a+b+c=360^\circ$

유형3

앞서 배운 유형을 확장하면 평행한 두 직선 $l,\;m$에 대하여 다음이 성립한다.

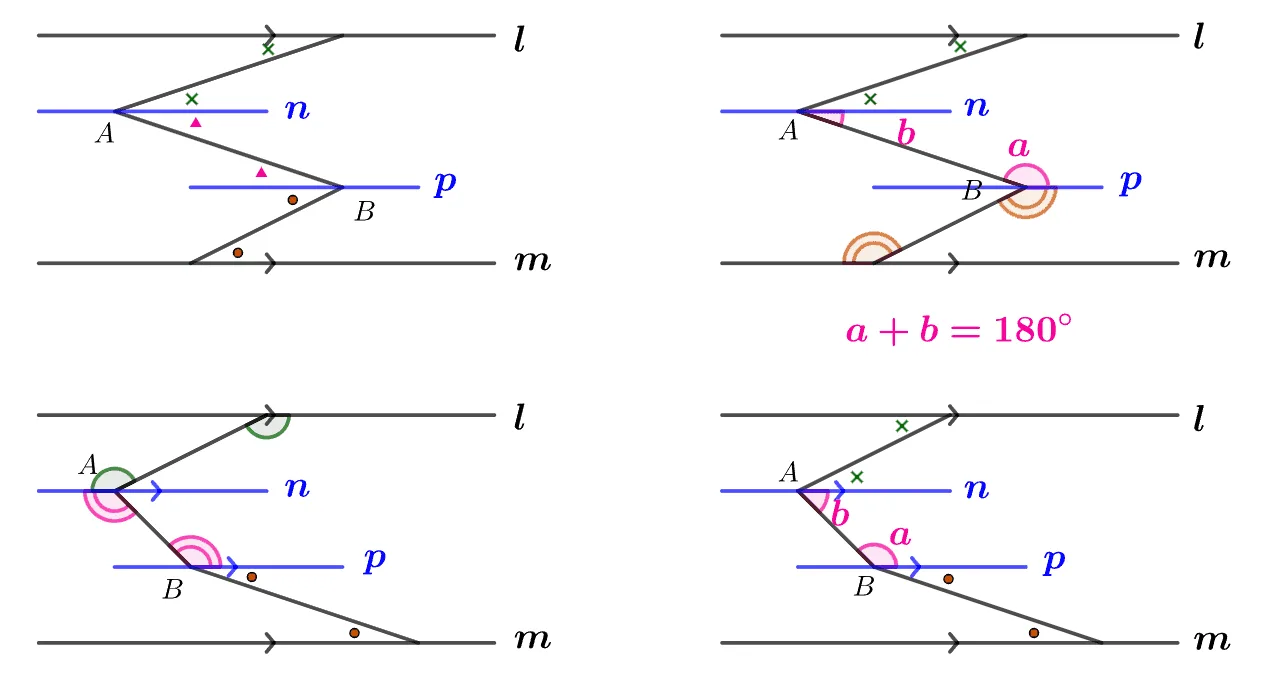
유형4 종이접기

평행선이 포함된 종이접기는 다음과 같은 특징을 갖는다.

• 접힌각은 크기가 같다.
• 동위각, 엇각의 크기가 같다.

위의 성질을 다음 문제를 통해 살펴보자.

직사각형 모양의 종이 $\square{ABCD}$를 접어서 만든 도형에 대하여$\angle{DEG}=a,\;\angle{AEF}=b$라고 할 때 $x,\;y$를 $a,\;b$에 대한 식으로 나타내어라.

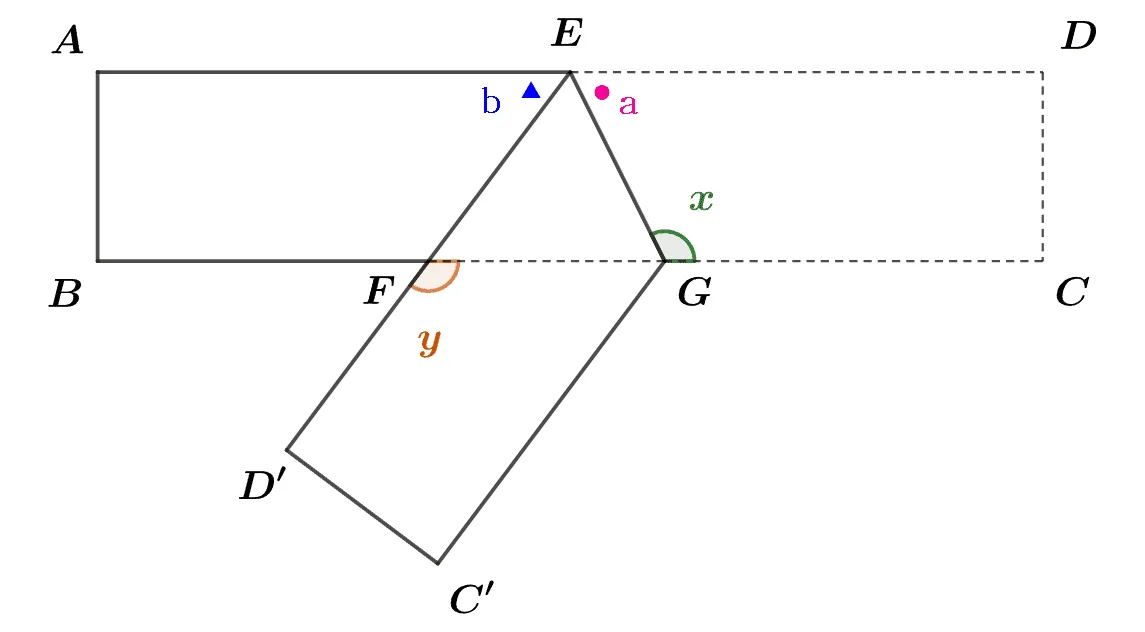
문제와 별개로 종이접기의 수학적 구조를 정확히 이해하기 위해 점 $E,\;F,\;G$의 교각을 모두 $a,\;b$로 나타내면 다음과 같다.

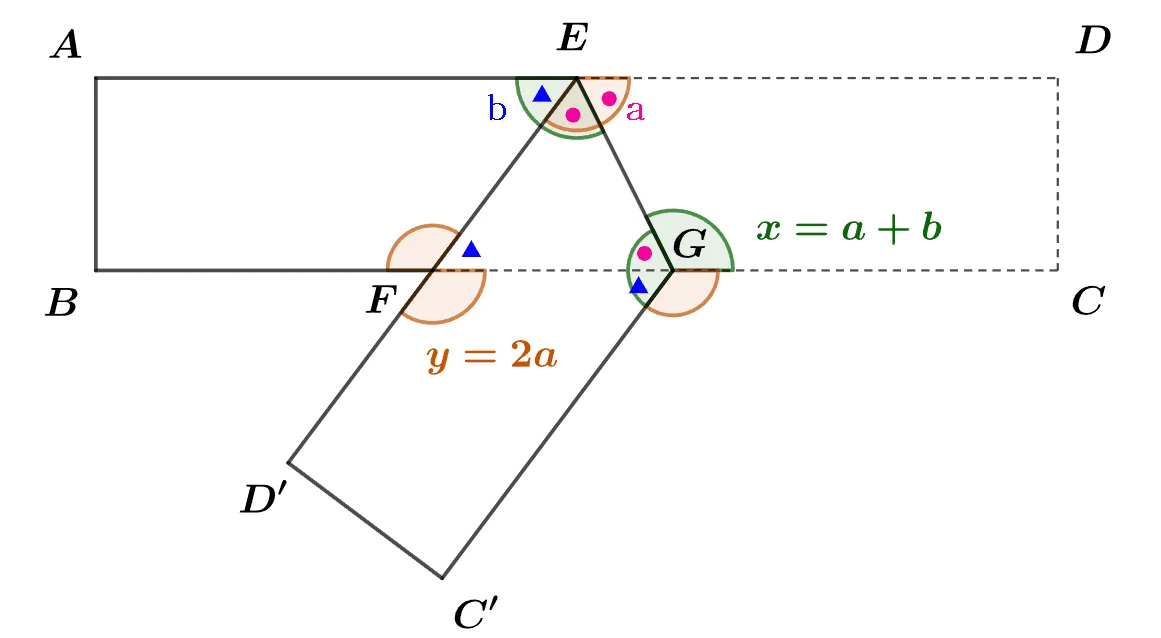
[풀이]

접힌각이 같아야 하므로 $\angle{GED’}=\angle{GED}=\angle{a}$이다.

• $\angle{x}=\angle{AEG}=b+a$ $\because$ 엇각
• $\angle{y}=\angle{DEF}=2a$ $\because$ 동위각

[추가 정리]

[1] 접힌각의 크기가 같다.

• $\angle{GED’}=\angle{GED},\;\angle{EGC’}=\angle{EGC}$

[2] $\triangle{EFG}$는 이등변 삼각형이다.

• $\angle{GEF}=\angle{DEG}\overset{\underset{\text{엇각}}{}}{=}\angle{EGF}$

심화 문제

평행한 두 직선 $l,\;m$에 대하여 $\angle{ABC}=125^\circ$이고 다음을 만족할 때$\angle{ADC}$의 크기를 구하여라.

• $3\angle{DAB}=2\angle{DAP}$
• $3\angle{BCQ}=5\angle{DCQ}$

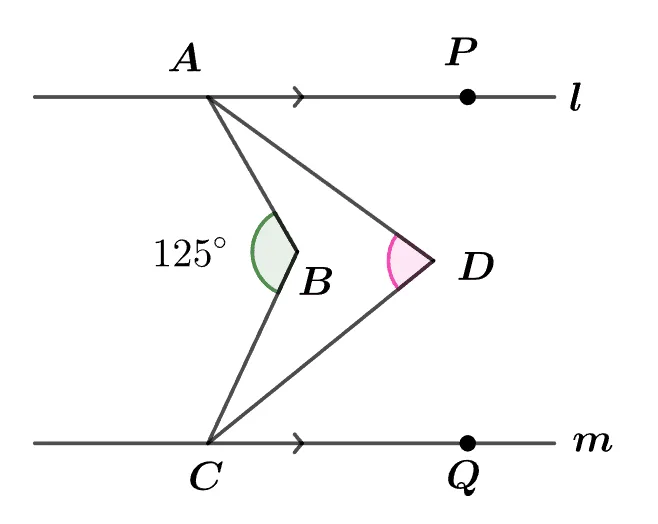
[풀이]

주어진 조건으로 부터 다음이 성립한다.

• $3\angle{DAB}=2\angle{DAP}$

$\angle{DAB}:\angle{DAP}=\dfrac{1}{3}:\dfrac{1}{2}=2:3$
$\angle{DAB}=2x,\;\angle{DAP}=3x$

• $3\angle{BCQ}=5\angle{DCQ}$

$\angle{BCQ}:\angle{DCQ}=\dfrac{1}{3}:\dfrac{1}{5}=5:3$
$\angle{BCQ}=5y,\;\angle{DCQ}=3y,\;\angle{BCD}=2y$

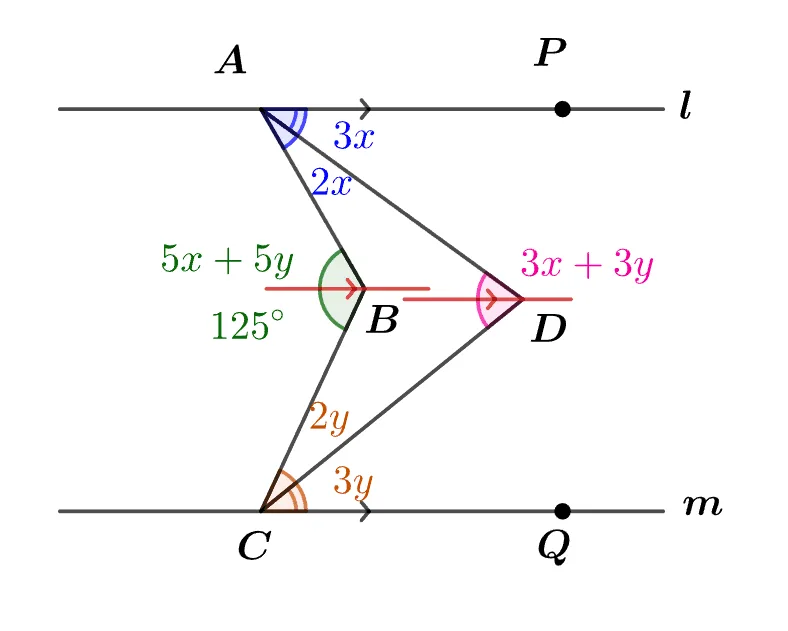
점 $B,\; D$를 지나고 직선 $l,\; m$과 평행한 보조선을 그리면 다음과 같은 결과를 얻을 수 있다.

• $\angle{ABC}=5x+5y=125^\circ$
• $\angle{ADC}=3x+3y$

$\angle{ADC}$는 $\angle{ABC}$의 $\dfrac{3}{5}$이므로 다음과 같이 구할 수 있다.

$\begin{align}\angle{ADC}&=\angle{ABC}\times \dfrac{3}{5}\\[1em]
&=125^\circ\times\dfrac{3}{5}=75^\circ\end{align}$

실생활 문제

카메라의 조리개를 조였을 때 오른쪽과 같이 작은 각들이 모여 점차적으로 $360^\circ$를 이루고 빛의 양을 줄여준다. 여기에는 동위각과 엇각의 원리가 숨어 있다.

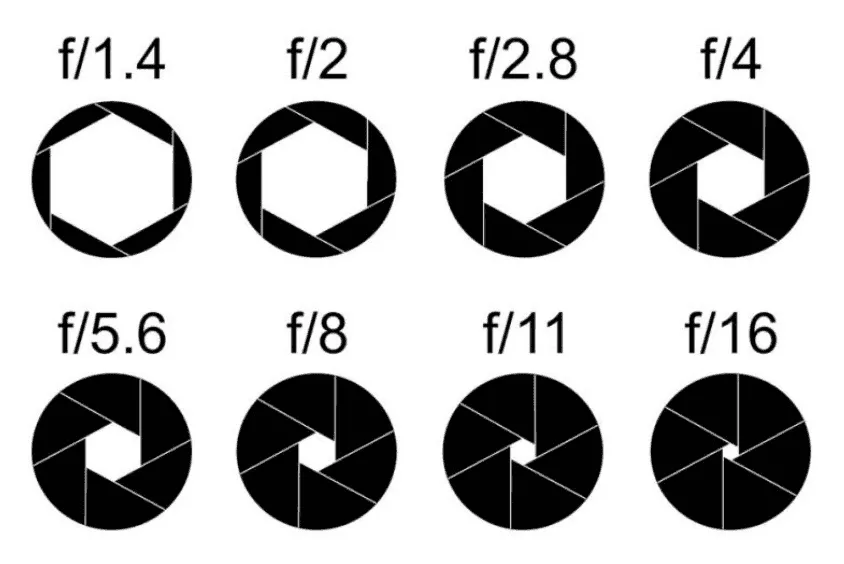
[문제] 평행한 두 직선 $l,\;m$에 대하여 $a+b+c+d+e+f$값을 구하여라.

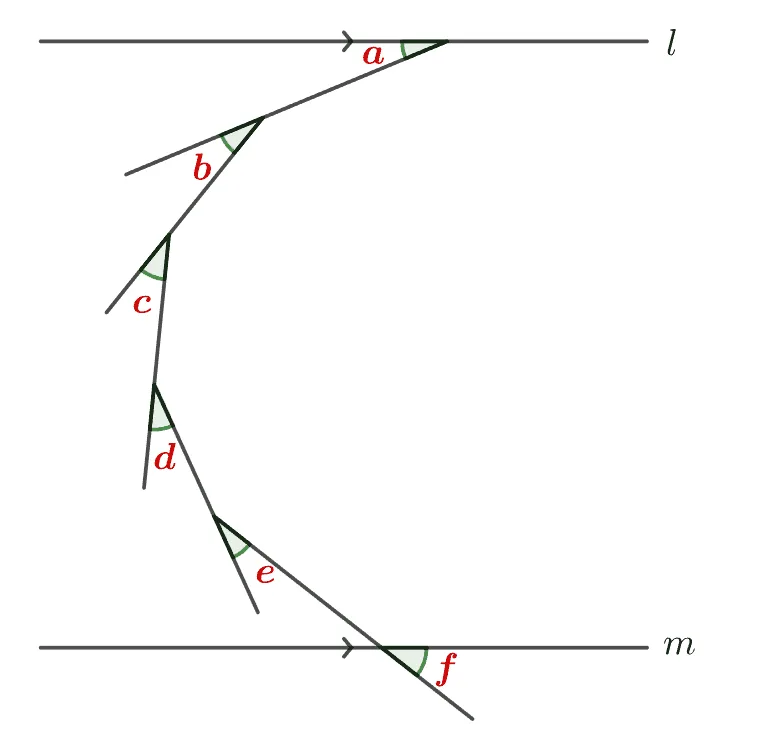
조리개의 구조를 이해하고 있다면 $a+b+c+d+e+f=180^\circ$임을 알 수 있다. 수학적으로 맞는지 확인해 보자.

[풀이]

주어진 각의 꼭짓점을 지나고 $l,\;m$에 평행인 보조선을 그리면 다음과 같이 동위각을 이용해 문제를 풀 수 있다.

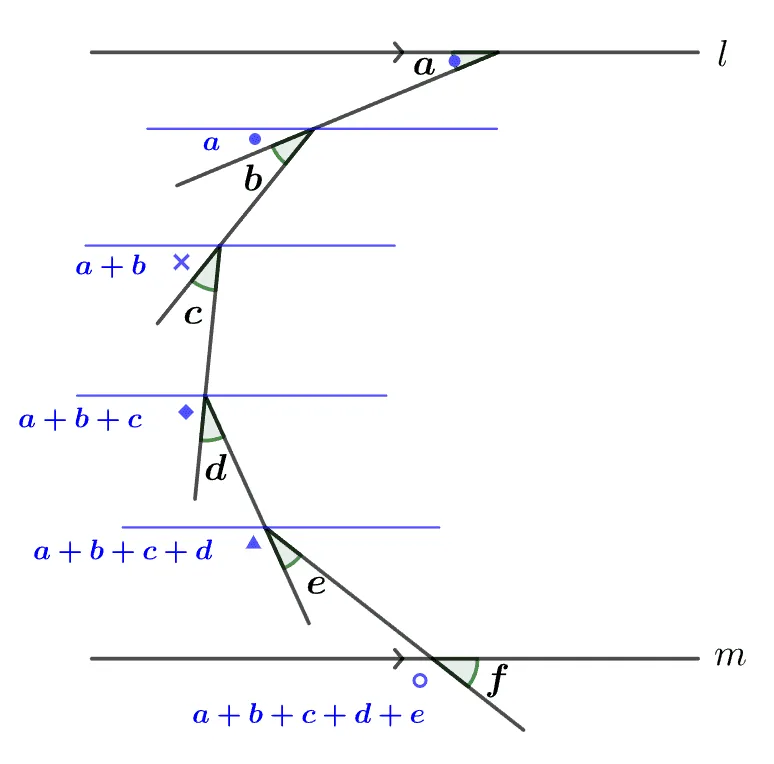
$\therefore \quad a+b+c+d+e+f=180^\circ$

이 사실은 앞으로 배울 정다각형의 외각의 크기 합이 $360^\circ$로 일정하다는 사실을 증명하는 과정의 일부이다.

맺음말

동위각 엇각의 성질을 이용하면 다양한 문제를 해결할 수 있습니다. 정리한 유형을 바탕으로 관련 문제를 찾아 해결해 보고 어떤 유형인지 정리해 보도록 합시다.