이 글에서는 다면체의 정의부터 다양한 종류인 각기둥, 각뿔, 각뿔대에 대해 설명하며, 이를 통해 다면체의 특징을 체계적으로 정리해보겠습니다. 또한, 스위스 수학자 오일러가 발견한 오일러 공식($v-e+f=2$)을 적용해, 각기둥과 각뿔 등의 도형에서 이 공식이 어떻게 성립하는지 살펴보도록 합시다.
목차
다면체 정의
다면체 : 다각형인 면으로만 둘러싸인 입체도형
- 면: 다면체를 둘러 싸고 있는 다각형
- 면의 최소 개수 : 4개 (사면체=삼각뿔)
- 이름: 면의 개수에 따라 $\rightarrow$ 사면체, 오면체, $\cdots$
- 모서리: 다면체를 이루는 다각형의 변
- 꼭짓점: 다면체를 이루는 다각형의 꼭짓점
주의 : 원기둥, 원뿔, 구 는 다면체가 아니다.
보충 설명
정의 적용

간단한 문제를 통해 다면체의 정의를 다시 정리해 보자.
- 다면체가 아닌 것은? 6
- 육면체인 것은? 1,2,3
입체도형의 면의 최소 개수

입체도형을 만들기 위해서 한 꼭짓점에 최소한 면이 3개 있어야하고, 사방이 둘러 싸인 입체를 만들기 위해서는 3개의 면으로 불가능하다. 따라서 최소 4개의 면이 필요하다.
볼록다면체, 오목다면체
다면체의 정의를 가지고 생각하면 위와 같은 입체도형은 모두 다면체 라고 할 수 있다. 하지만 학교 수학에서는 볼록다면체만 다룬다.(첫 번째, 두 번째)
다면체 종류
다면체의 대표인 각기둥, 각뿔, 각뿔대에 대해 살펴보자.
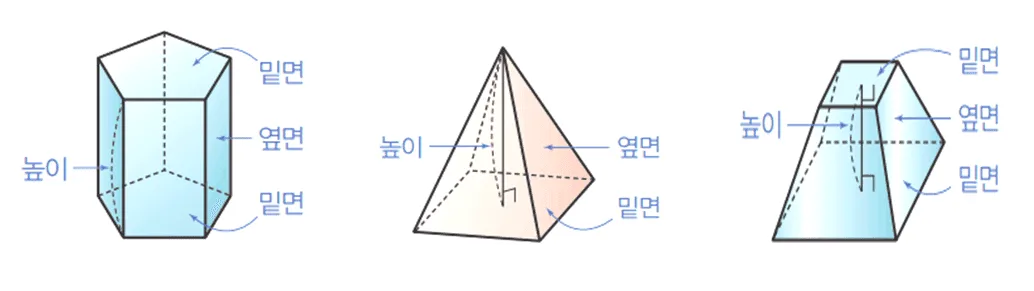
각기둥
- 밑면: 두 개의 합동, 평행인 다각형
- 옆면: 직사각형
- 높이: 평행한 두 밑면 사이의 거리
- 이름: 밑면이 $n$각형 $\rightarrow$ $n$각기둥
각뿔
- 밑면: 다각형 (하나)
- 옆면: 삼각형
- 높이: 각뿔의 꼭짓점에서 밑면까지 거리
- 이름: 밑면이 $n$각형 $\rightarrow$ $n$각뿔
각뿔대
각뿔을 밑면에 평행한 평면으로 자를 때 생기는 입체도형 중 각뿔이 아닌 것
- 밑면: 서로 평행한 다각형
- 옆면: 사다리꼴
- 높이: 평행한 두 밑면 사이의 거리
- 이름: 밑면이 $n$각형 $\rightarrow$ $n$각뿔대
오일러 공식(Leonhard Euler)
1752년 스위스 수학자 오일러는 입체도형에서 꼭짓점($v$), 모서리($e$), 면($f$)을 다음과 같이 계산하면 항상 일정한 수 (2)가 나오는 것을 발견하였다.
$v-e+f=2$
- $v$: vortex 꼭짓점
- $e$: edge 모서리
- $f$: face 면
오일러 공식 적용
각기둥, 각뿔, 각뿔대에 대하여 오일러 공식을 적용해 보자.
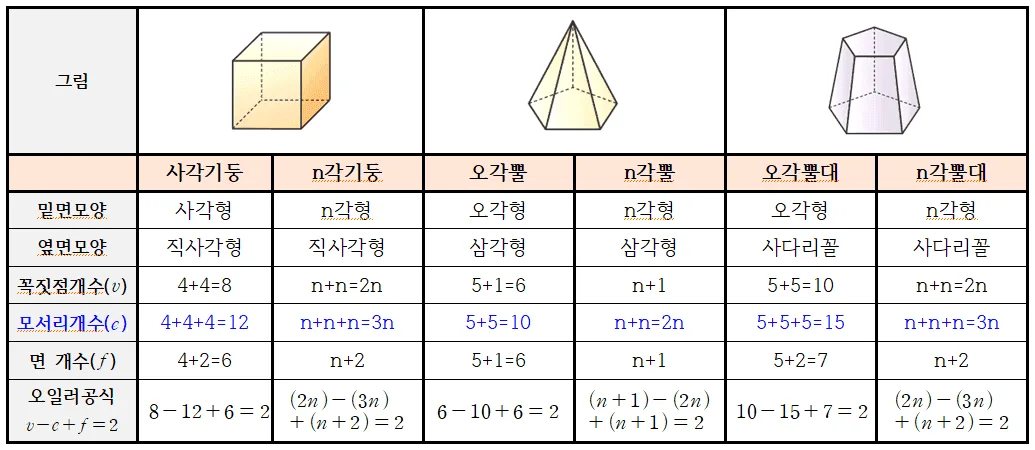
$n$각기둥
- 꼭짓점 개수 : $2n$
- 모서리 개수 : $3n$
- 면의 개수 : $n+2$
오일러 공식 적용 : $v-e+f=(2n)-(3n)+(n+2)=2$
$n$각뿔
- 꼭짓점 개수 : $n+1$
- 모서리 개수 : $2n$
- 면의 개수 : $n+1$
오일러 공식 적용 : $v-e+f=(n+1)-(2n)+(n+1)=2$
$n$각뿔대
- 꼭짓점 개수 : $2n$
- 모서리 개수 : $3n$
- 면의 개수 : $n+2$
오일러 공식 적용 : $v-e+f=(2n)-(3n)+(n+2)=2$
이상으로 다면체와 오일러 정리에 대한 학습을 마무리 하도록 하겠습니다.
