다각형은 평면도형의 가장 기본적인 도형으로 이번시간에는 다각형의 용어정리를 시작으로 대각선의 개수 내각 및 외각의 합에 대하여 알아보려고 합니다. 일반적인 n각형에 대한 공식에 이르기 까지의 과정을 잘 이해하길 바랍니다.
목차
다각형 용어 정리
다음 그림을 이용해 다각형과 관련된 용어에 대해 정리해 보자.
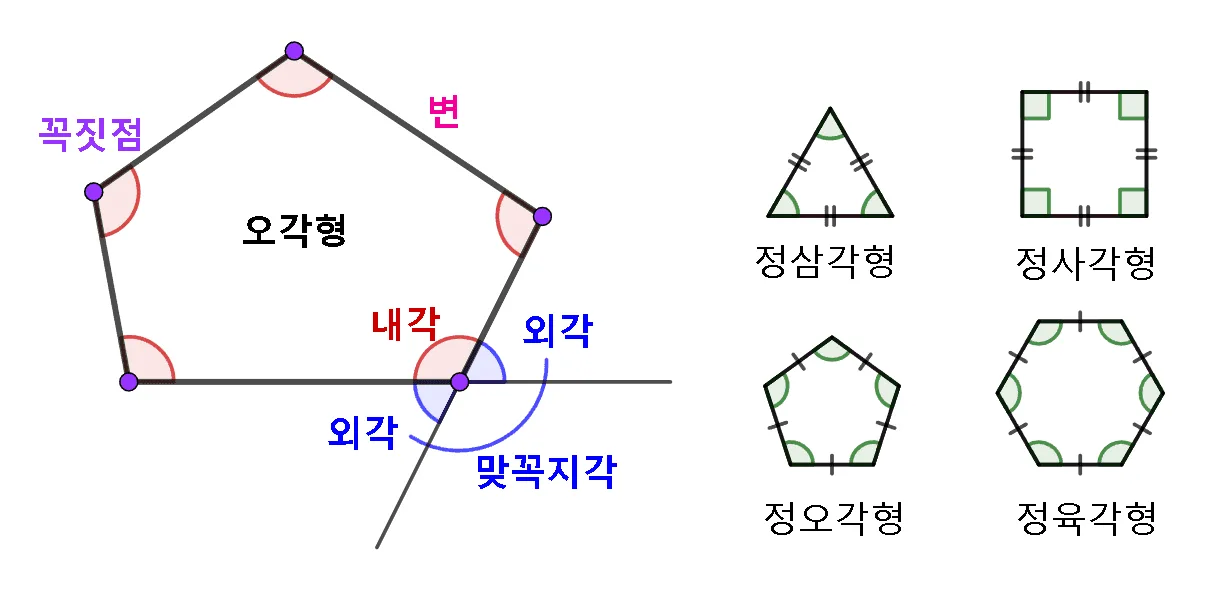
- 다각형: 선분으로 둘러 싸인 평면도형
변의 개수에 따라 삼각형, 사각형, $\cdots$, n각형- 변: 다각형을 이루는 각 선분
- 꼭짓점: 다각형에서 변과 변이 만나는 점
- 내각: 이웃하는 두 변으로 이루어진 내부의 각
- 외각: 각 꼭짓점에서 한 변과 다른 변의 연장선으로 이루어진 각
- 정다각형: $\bbox[#ffff00]{\text{모든 변}}$의 길이가 같고, $\bbox[#ffff00]{\text{모든 내각}}$의 크기가 같은 다각형
변의 개수에 따라 정삼각형, 정사각형 $\cdots$ 정n각형
다각형의 외각은 한 꼭짓점에 두 개 있고 맞꼭지각으로 크기가 동일하므로 하나만 생각한다.
- 내각과 외각 사이의 관계
- 내각$+$외각$=180^\circ$
다각형의 대각선 개수
오각형과 육각형에서 직접 대각선을 그려보고 개수를 세어보면 다음과 같다.
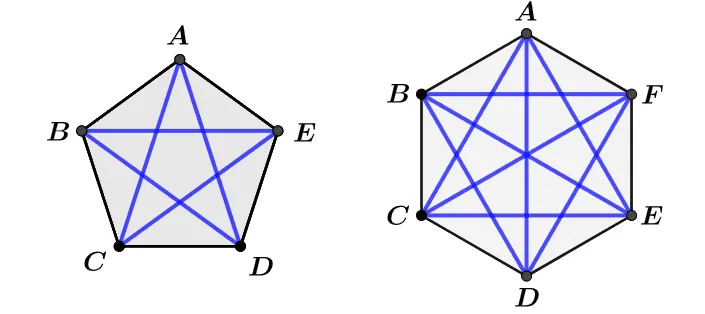
위의 그림을 통해 변의 개수가 많은 다각형일 수록 대각선의 개수를 직접 세기 어려워 짐을 알 수 있다. 7각형, 8각형, $\cdots$ n각형의 대각선의 개수를 쉽게 구할 수 있는 방법에 대해 알아보자.
n각형의 대각선 개수 증명
오각형을 이용해서 일반적인 다각형 (n각형)의 대각선의 개수를 구하는 방법에 대해 정리해보자.

한 꼭짓점에서 대각선 개수
오각형을 기준으로 $\bbox[#ffff00]{\text{한 꼭짓점에서 그릴 수 있는 대각선 개수}}$와 이 때 만들어지는 $\bbox[#dcff8c]{\text{삼각형 개수}}$를 정리하면 다음과 같다.
- 한 꼭짓점(A)에서 그릴 수 있는 대각선 개수
- $\bbox[#ffff00]{\text{대각선 개수}}$ : $5-{\color{red}3}\xrightarrow[]{\text{n 각형}}n-{\color{red}3}$
- ${\color{red}3}$ : A에서 대각선을 그릴 수 없는 꼭짓점 개수
- 자신(A)과 이웃한 꼭짓점(B,E)
- 한 꼭짓점(A)에서 대각선으로 그릴 때 삼각형의 개수
- $\bbox[#dcff8c]{\text{삼각형 개수}}$ : $(\bbox[#ffff00]{\text{대각선 개수}})+{\color{blue}1}$$\xrightarrow[]{\text{n 각형}} (\bbox[#ffff00]{n-3})+{\color{blue}1}=\bbox[#dcff8c]{n-2}$
- ${\color{blue}1}$ : 대각선의 개수 보다 하나 더 생긴다.
n각형의 대각선 개수
오각형에서 각 꼭짓점에서 대각선을 두 개씩 그릴 수 있고, 꼭짓점에서 중복을 허용하여 대각선을 그리면 모두 두 번씩 그려진다. 따라서 다각형의 대각선의 개수는 $\bbox[#ffff00]{\text{한 꼭짓점 대각선 개수}}\times \bbox[#94feff]{\text{꼭짓점 개수}}$를 계산하고 $\bbox[#dcff8c]{\text{중복된 횟수}}$로 나누어 구할 수있다.
$\dfrac{\bbox[#ffff00]{\text{한 꼭짓점 대각선 개수}}\times \bbox[#94feff]{\text{꼭짓점 개수}}}{\bbox[#dcff8c]{2\text{ : 중복}}}$
이를 문자로 정리하면 아래와 같다.
- ($\bbox[#ffc5fd]{\text{n각형의 대각선 개수}}$)$=\dfrac{(\bbox[#ffff00]{n-{\color{red}3}}) \times \bbox[#94feff]{n}}{\bbox[#dcff8c]{2}}\\[1em]$
- $(\bbox[#ffff00]{n-{\color{red}3}})$ : 한 꼭짓점에서 그릴 수 있는 대각선의 개수
- $\bbox[#94feff]{n}$ : 꼭짓점 개수
- $\bbox[#dcff8c]{2}$: 중복
삼각형의 내각과 외각(n=3)
초등학교에서는 다음과 같이 삼각형을 잘라서 세 내각의 합이 $180^\circ$임을 보인다. 이는 실험적 방법으로 수학적인 방법은 아니다.
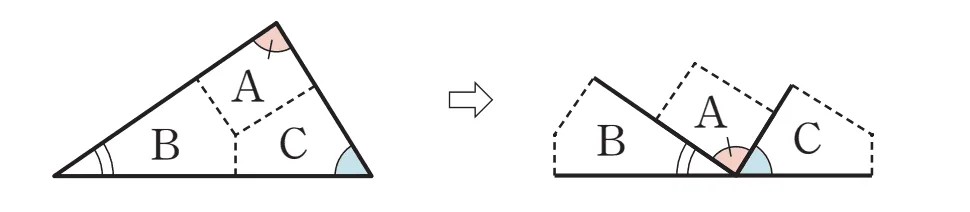
이제 다음의 사실을 수학적으로 증명해 보기로 하자.
- 삼각형의 세 내각의 합은 $180^\circ$이다.
실험적 방법에서 처럼 세 각을 한 곳에 모아서 증명 할 수 있다. 평행선을 이용해 각을 한 곳으로 모으면 아래와 같은 결과를 얻을 수 있다.
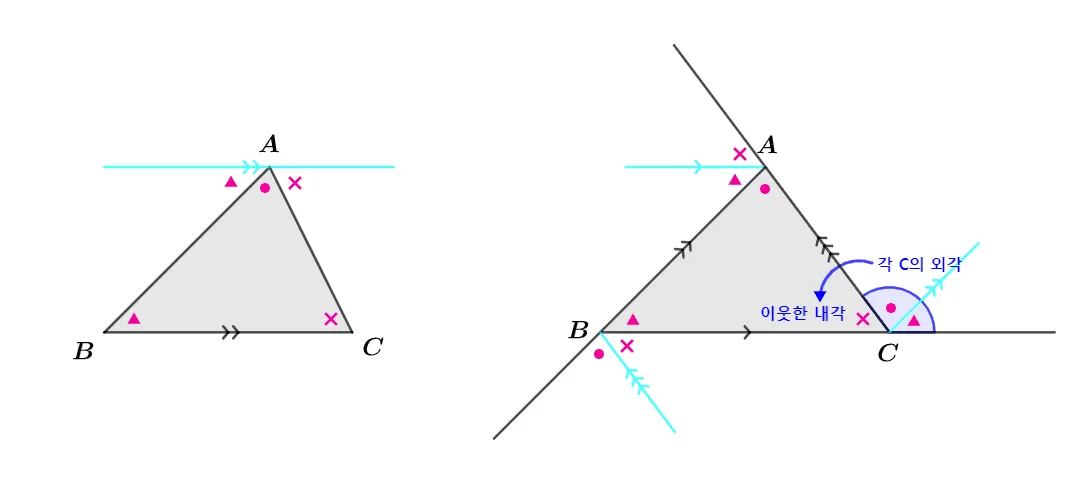
오른쪽의 증명에서는 다음과 같은 $\bbox[#ffff00]{\text{외각의 성질}}$을 추가로 알 수 있다.
- 한 외각의 크기는 이웃하지 않은 두 내각의 합과 같다.
- 세 외각의 크기 합은 $360^\circ$이다.
다각형 (n각형)의 내각과 외각
다각형 (n각형)의 내각의 크기의 합
결과 부터 정리하면 다각형의 내각의 크기의 합은 다음과 같다.
- $180^\circ\times (n – 2)$
위의 사실을 세 가지 방법으로 증명해 보자.
대각선을 이용한 증명
먼저 가장 일반적인 대각선을 이용한 증명부터 살펴보자.
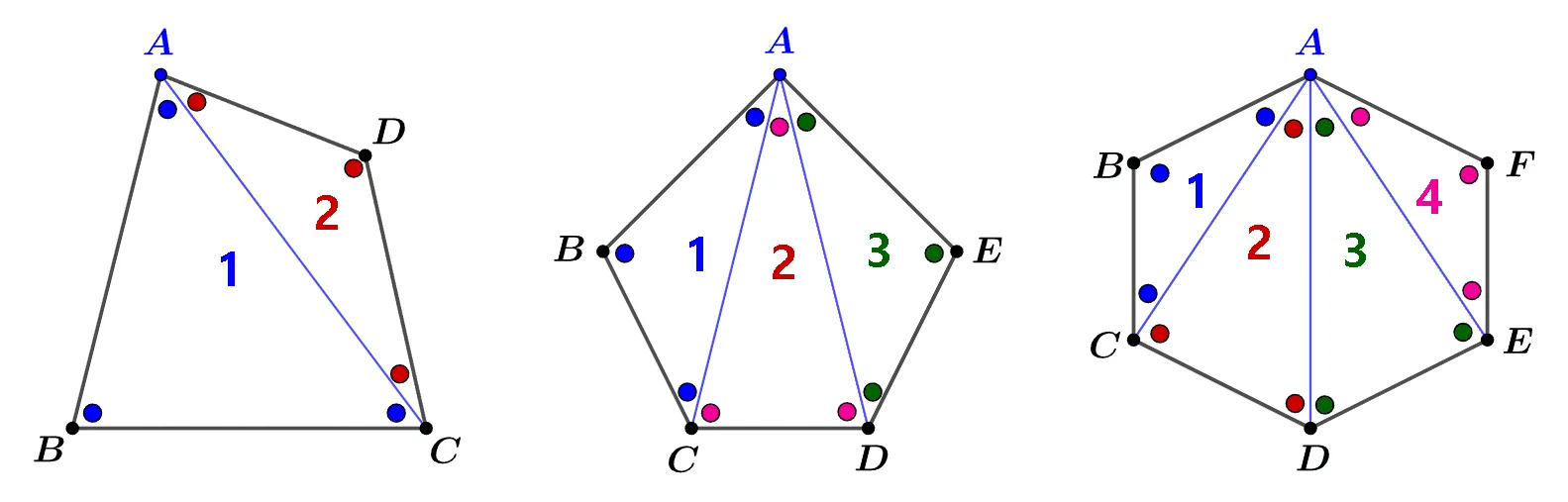
다각형의 한 꼭짓점에서 대각선을 그으면 다각형을 삼각형으로 나눌 수 있고 삼각형의 내각의 크기를 합하면 다각형의 내각의 크기의 합과 일치한다. 따라서 다음과 같이 정리 할 수 있다.
[n각형의 내각의 크기의 합]
$180^\circ \times (\bbox[#ffff00]{\text{삼각형의 개수}})=180^\circ \times (\bbox[#ffff00]{n-2})$
다른 증명 방법
다각형의 내각의 크기의 합을 증명하는 다른 두 가지 방법에 대해 정리해 보자.
- 내부의 점을 이용한 증명
- 변 위의 점을 이용한 증명
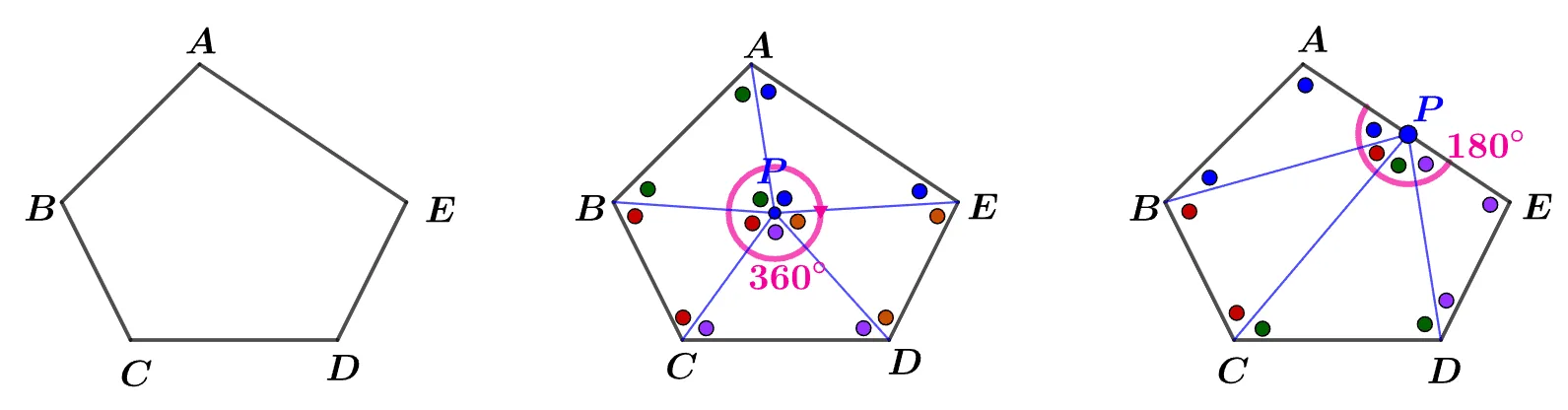
내부의 점을 이용한 증명
두 번째 그림에서 내부의 점 $P$와 각 꼭짓점을 연결한 $\bbox[#dcff8c]{5}$개의 삼각형에 대하여 다음과 같이 오각형의 내각의 합을 계산 할 수 있다.
- $\bbox[#ffff00]{180^\circ}\times \bbox[#dcff8c]{5}-\bbox[#94feff]{360^\circ}$
주어진 식에서 $\bbox[#ffff00]{\text{삼각형의 내각의 합}}$, $\bbox[#dcff8c]{\text{삼각형의 개수}}$, $\bbox[#94feff]{\text{제외할 각의 크기}}$를 n각형으로 확장하여 다음과 같이 내각의 합을 구할 수 있다.
[n각형의 내각의 크기의 합]
- $\bbox[#ffff00]{180^\circ}\times \bbox[#dcff8c]{n}-\bbox[#94feff]{360^\circ}=180^\circ\times (n-2)$
변 위의 점을 이용한 증명
$\overline{AE}$위의 점 $P$에서 각 꼭짓점을 연결하면 $4$개의 삼각형이 만들어 지고 다음과 같이 내각의 합을 계산 할 수 있다.
- $\bbox[#ffff00]{180^\circ}\times \bbox[#dcff8c]{4}-\bbox[#94feff]{180^\circ}$
주어진 식에서 $\bbox[#ffff00]{\text{삼각형의 내각의 합}}$, $\bbox[#dcff8c]{\text{삼각형의 개수}}$, $\bbox[#94feff]{\text{제외할 각의 크기}}$를 n각형으로 확장하여 다음과 같이 내각의 합을 구할 수 있다.
[n각형의 내각의 크기의 합]
- $\bbox[#ffff00]{180^\circ}\times (\bbox[#dcff8c]{n-1})-\bbox[#94feff]{180^\circ}=180^\circ\times (n – 2)$
다각형 (n각형)의 외각의 크기의 합
결과 부터 정리하면 다음과 같다.
- 다각형의 외각의 크기의 합은 $360^\circ$로 일정하다.
위의 사실을 두 가지 방법으로 증명해 보자.
대수적 증명
(내각)$+$(외각)$=180^\circ$이므로
$n$각형에 대하여
- $\bbox[#ffff00]{\text{내각의 합}}+\bbox[#dcff8c]{\text{외각의 합}} =180^\circ \times n$
- $(\because \;\text{내각 + 외각}=180^\circ)$
- $\bbox[#ffff00]{\text{내각의 합}}=180^\circ\times (n-2)^\circ$
$\therefore\;180^\circ\times n-360^\circ$
따라서 외각의 합은 다음과 같다.
- $\bbox[#dcff8c]{\text{외각의 합}} =360^\circ$ (일정)
기하적 증명
다각형의 외각의 크기의 합에 대한 기하적 증명은 오각형에 대해 직관적으로 보여 보자.
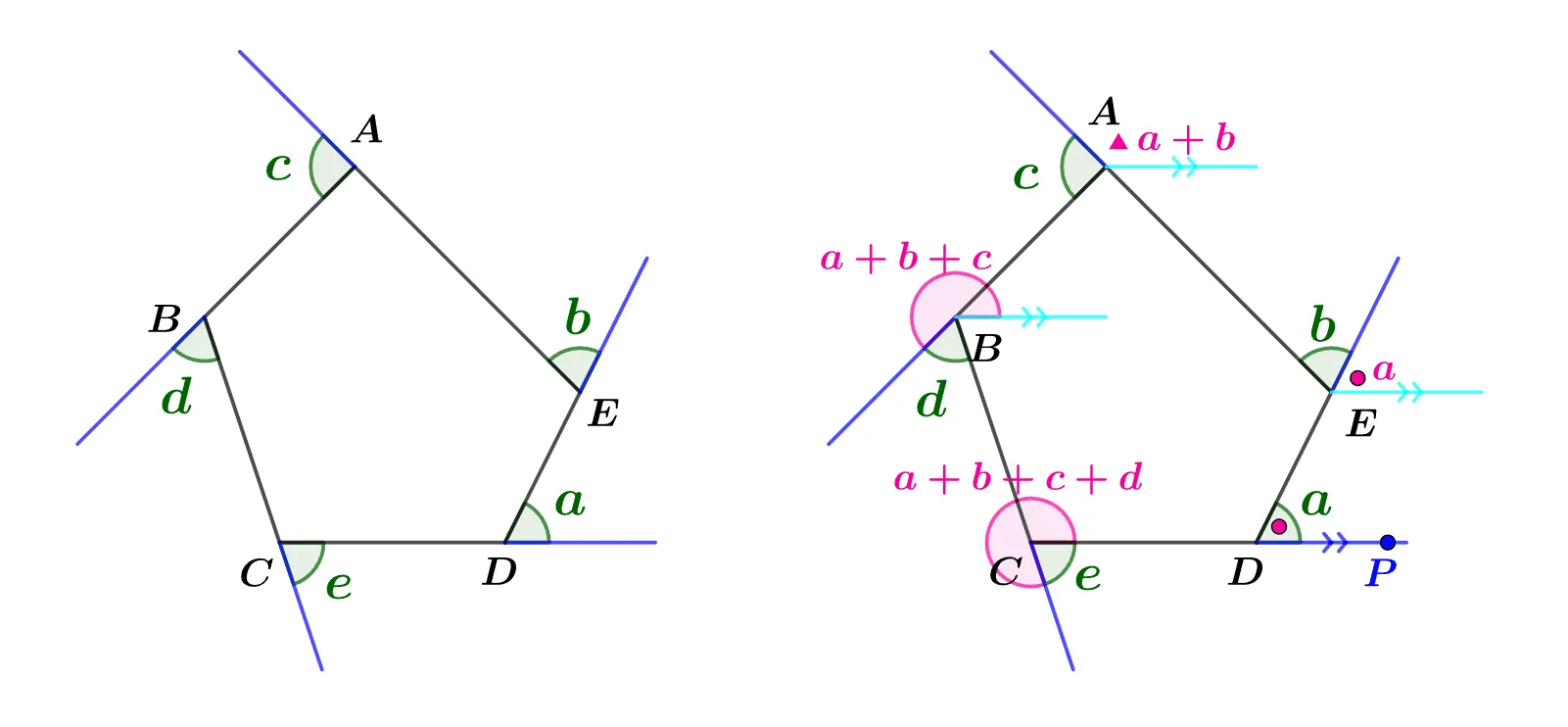
꼭짓점 D의 외각에 대한 연장선 $\overline{DP}$에 평행하고 꼭짓점 $A,\;B,\;E$를 지나는 $\bbox[#94feff]{\text{평행선}}$에 대하여 동위각 엇각의 성질을 적용하면 $a+b+c+d+e=360^\circ$임을 알 수 있다.
정다각형 (정n각형)의 내각과 외각
먼저 다각형의 내각과 외각에 대한 공식을 정리하면 아래와 같다.
- n각형 내각의 크기의 합
- $\bbox[#ffff00]{180^\circ\times (n -2)^\circ}$
- n각형 외각의 크기의 합
- $\bbox[#dcff8c]{360^\circ}$ (일정)
- 정다각형도 다각형이므로 위의 성질을 만족한다.
정다각형 (정n각형)에서 추가적으로 다음과 같은 사실도 성립한다.
- 정n각형의 $\bbox[#ffc5fd]{\text{한}}$ 내각의 크기
- $\dfrac{\bbox[#ffff00]{180^\circ\times (n-2)}}{\bbox[#ffc5fd]{n}}$ ($\bbox[#ffc5fd]{n}$: 꼭짓점 개수)
- 정n각형의 $\bbox[#ffc5fd]{\text{한}}$ 외각의 크기
- $\dfrac{\bbox[#dcff8c]{360^\circ}}{\bbox[#ffc5fd]{n}}$ ($\bbox[#ffc5fd]{n}$: 꼭짓점 개수)
다각형의 내각과 외각 정리
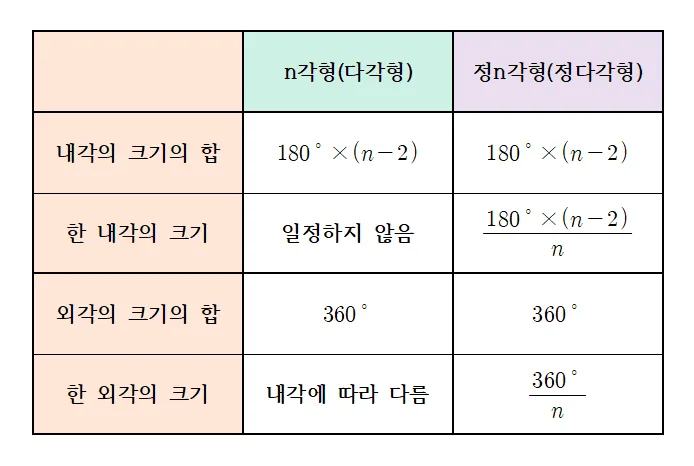
앞서 학습한 내용을 정리하면 다음과 같다.
맺음말
다각형의 내각과 외각, 대각선의 개수를 구하는 공식은 다양한 수학문제를 해결하는데 사용됩니다. 이 공식을 유도하는 과정에 필요한 수학적 사고 또한 여러 수학개념에서 공통적으로 사용되고 있으므로 꼭 먼저 이해하고 암기하길 바랍니다.
