이 글에서는 지도에 사용되는 원통 투영법(cylinder projection)과 중학교 삼각형의 닮음을 이용해 구의 겉넓이를 증명하는 방법에 대해 다루었습니다. 구의 표면을 원기둥의 옆면에 투영하는 과정과, 그로 인해 구의 겉넓이 공식 $4\pi r^2$으로 계산되는 과정에 대해 정리해 봅시다.
목차
원통 투영법 cylinderical projection


원통 투영법(cylinderical projection)을 이용하면 구를 원기둥의 옆면에 투영하여 지도를 만들수 있다. 이 투영법의 성질은 다음과 같다.
- (구 표면의 직사각형)$=$(원기둥 옆면의 직사각형 그림자)
위의 성질을 증명하면 구의 겉넓이를 기둥의 옆넓이로 구할 수 있다.
- (구의 겉넓이)=(기둥의 옆넓이)
$\therefore\; 2\pi r\times 2r=4\pi r^2$
구면 직사각형과 그림자의 넓이
구면을 매우 작은 사각형 모양으로 자르면 노란색 도형은 직사각형에 가까워 진다. 따라서 구면의 직사각형과 그 그림자(원기둥의 직사각형 모양)의 넓이가 같음을 보이면 충분하다.
직사각형 가로 비율(닮음)
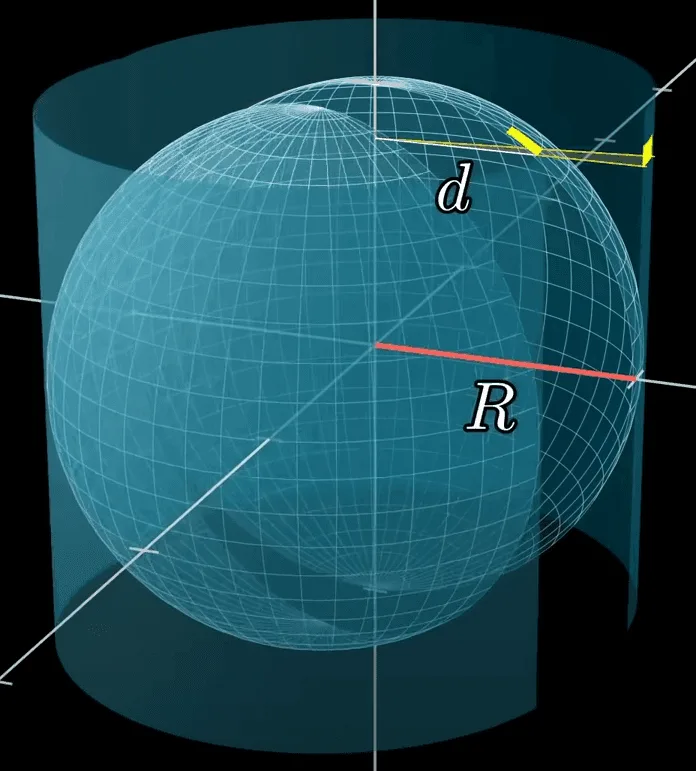
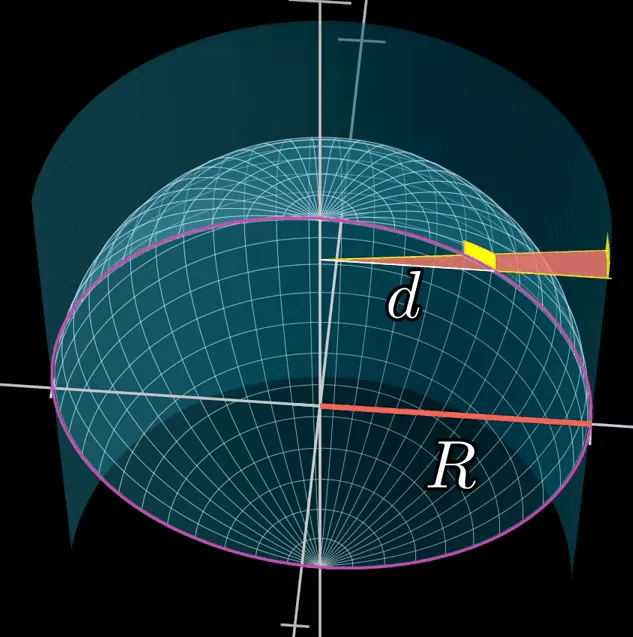
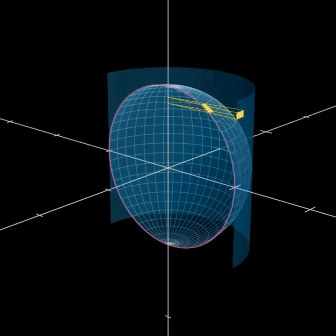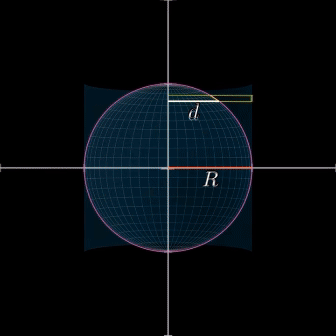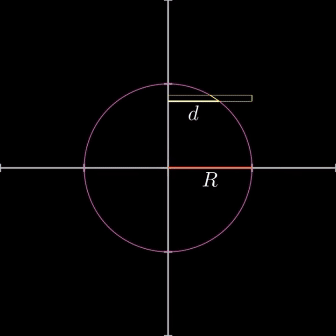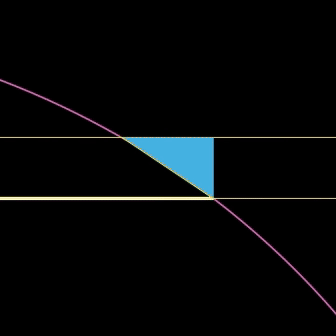
반지름이 $r$인 구면의 직사각형이 광원에서 $d$만큼 떨어져 있다고 할 때 위 쪽에서 내려다 본 모양은 다음과 같다.
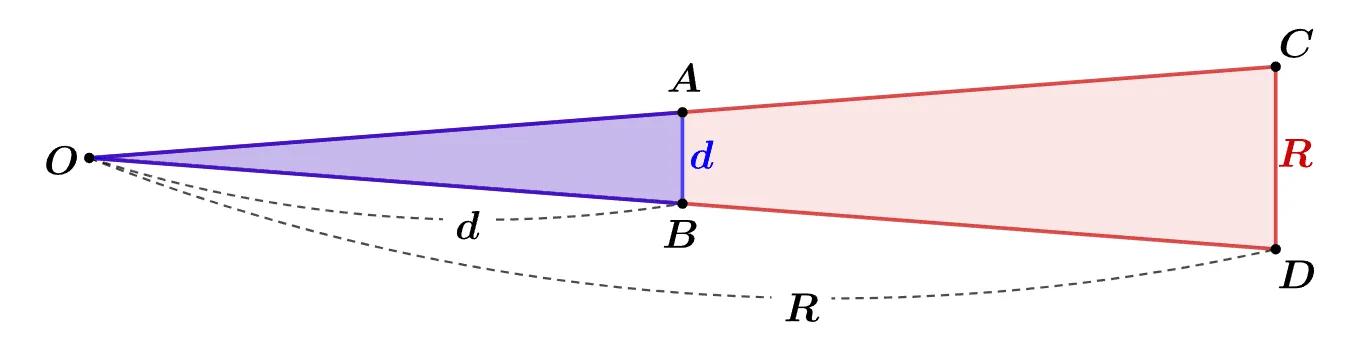
두 직사각형은 서로 확대, 축소 관계에 있다. (닮음 중2) 따라서 다음이 성립한다.
- 닮음비 : 확대 축소 비율
- $\triangle{OAB}∽\triangle{OCD}$
- $\overline{AB}:\overline{CD}=d:R$
직사각형 세로 비율(닮음)
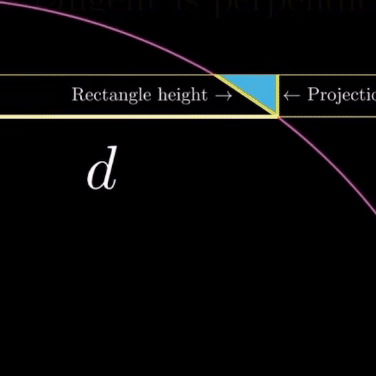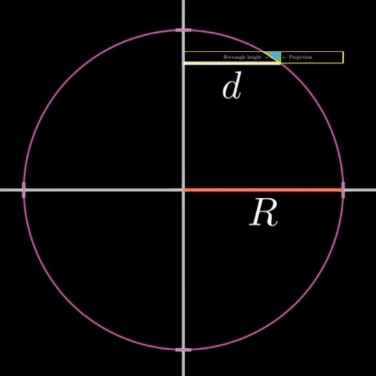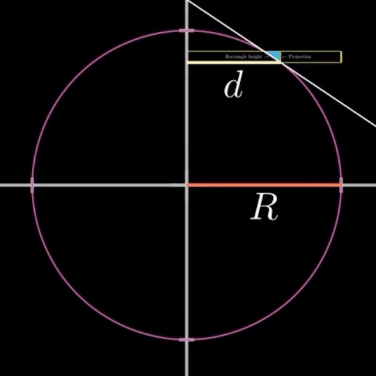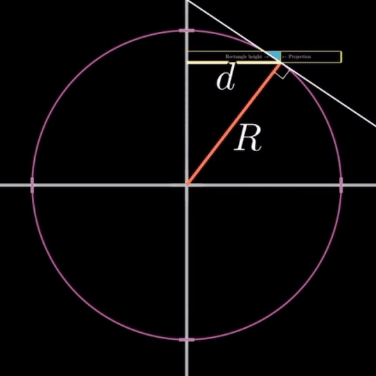
구면 위의 직사각형의 높이와 그림자(Projection)의 높이 사이 관계에 대해 정리해 보자.
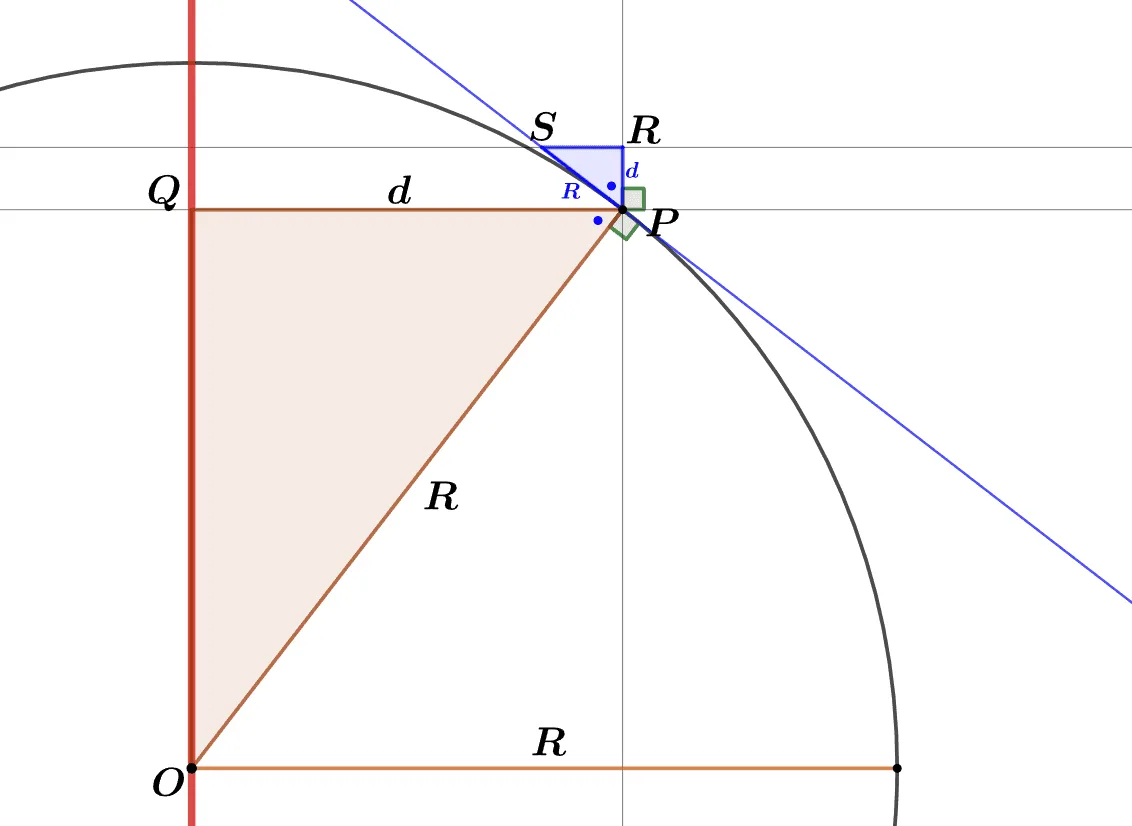
$\triangle{POQ} ∽ \triangle{PSR}$ (AA닮음)
- $\angle{PQO}=\angle{PRS}=90^\circ$
- $\angle{OPQ}=\angle{SPR}=\textcolor{blue}{\bullet}$
- $\angle{SPO}=\angle{QPR}=90^\circ$
- $\angle{SPQ}$: 공통
$\therefore\; \overline{OP}:\overline{PQ}=\overline{SP}:\overline{PR}=R:d$
넓이 비교
위의 결과를 정리하면 다음과 같다.
- ($\colorbox{#ffff00}{구면}$ 직사각형 가로) : ($\colorbox{#dcff8c}{그림자}$ 가로) $=d:R$
- ($\colorbox{#ffff00}{구면}$ 직사각형 세로) : ($\colorbox{#dcff8c}{그림자}$ 세로) $=R:d$
따라서 각 변의 길이를 다음과 같이 둘 수 있고 넓이가 같음을 알 수 있다.
- ($\colorbox{#ffff00}{구면}$ 직사각형 가로), ($\colorbox{#dcff8c}{그림자}$ 가로)를 각각 $\bbox[#ffff00]{dx},\bbox[#dcff8c]{Rx}$
- ($\colorbox{#ffff00}{구면}$ 직사각형 세로), ($\colorbox{#dcff8c}{그림자}$ 세로)를 각각 $\bbox[#ffff00]{Ry},\bbox[#dcff8c]{dy}$
($\colorbox{#ffff00}{구면}$의 사각형 넓이)=(원기둥의 $\colorbox{#dcff8c}{그림자}$ 넓이)$=dxRy$
구의 겉넓이 공식
위의 결과를 구면을 나눈 모든 사각형에 적용하면 구의 겉넓이가 기둥의 옆넓이와 같음을 알 수 있다. 이 사실을 수식으로 정리하면 다음과 같다.

(구의 겉넓이)=(기둥의 옆넓이)
$\therefore\; 2\pi r\times 2r=4\pi r^2$
구의 겉넓이가 구를 둘러싼 원기둥의 옆넓이와 같다는 사실을 이용해 구의 겉넓이를 구하는 공식이 $4\pi r^2$임을 증명하였습니다.
