곱셈공식을 문자로 암기하였다면 잘 못된 방법이므로 곱셈공식과 곱셈공식 암기법을 다시 정리할 필요가 있다. 곱셈공식 안에는 수학의 연산 구조가 들어 있고 이러한 연산 구조가 반영된 말로 설명할 수 있도록 하는 것이 이번 학습의 목표이다. 이번 기회를 통해 수식의 구조를 통찰할 수 있는 능력을 기르길 바란다.
목차
곱셈공식 중학교 3학년
제곱공식
- $(a+b)^2=a^2+2ab+b^2$
- $(a-b)^2=a^2-2ab+b^2$
분배법칙을 적용하면 다음과 같이 전개 할 수 있다.
$(a+b)^2$
$=(a+b)(a+b)$
$\rightarrow a^2+2ab+b^2$
이 식의 구조에 대해 더 자세히 학습해 보자.
$a$ 와 $b$를 $\triangle$, $\square$로 두면
$(\triangle + \square)^2=\triangle^2 +2\triangle \square +\square^2$
이를 말로 표현하면
두 식의 합을 제곱($(\triangle + \square)^2$) 하면
각 식의 제곱 ($\triangle^2,\square^2$)과
각 식을 곱한것의 두 배($2\times \triangle \times \square$)를 합한 것과 같음을 알 수 있다.
첫 번째 식의 $b \rightarrow -b$이면
식의 구조를 $(a-b)^2 \rightarrow \{a+(-b)\}^2$로 변형하면
첫 번째 공식을 이용해 두 번째 식을 유도 할 수 있다.
$\{a+(-b)\}^2$
$=a^2+2(a)(-b)+(-b)^2$
$=a^2-2ab+b^2$
제곱공식 암기법
두 식을 합하여 제곱하면 각 식의 제곱과 각 식의 곱의 두 배를 합한 것과 같다.
별로 달라 보이지 않지만 이렇게 이해하는 것이 구조를 이해하는 것이고 복합한 식을 인수분해 할 때 훨씬 유리하다.
문자로 암기하면 문자가 바뀌거나 숫자와 문자가 복잡한 상황에서 식을 유연하게 다루기 어렵기 때문이다.
합차공식
$(a-b)(a+b)=a^2-b^2$
전개를 하면 오른쪽의 결과를 얻을 수 있으므로 여기서는 암기법만 소개하고 다음으로 넘어가자.
합차공식 암기법
부호 반대인 부분을 $\square, \; \blacksquare$로 구분하여 표현하면 다음과 같다.
$(\triangle+\square)(\triangle+\blacksquare) = \triangle^2-\square^2$
이를 말로 표현하면 다음과 같다.
부호가 일정한 부분과 부호가 반대인 부분이 있는 두 식을 곱하면
$(부호동일)^2-(부호반대)^2$이다.
[예제] $(x^2+x+1)(x^2-x+1)$ 식을 전개하여라.
[풀이]
$(x^2+x+1)(x^2-x+1)$
$=(부호동일)^2-(부호반대)^2\; \because\;합차공식$
부호동일 : $(x^2+1)$
부호반대 : $x$
$(준식)=(x^2+x+1)(x^2-x+1)$
$=(x^2+1)^2-x^2\;\cdots(1)$
$(x^2+1)^2$
$=(x^2)^2+2\times x^2\times 1+1^2$
$=x^4+2x^2+1\;\cdots(2)$
$(2)\rightarrow (1) \; ; \;(준식) = x^4+x^2+1$
이차방정식 공식
$(x+a)(x+b)$
먼저 $(x+a)(x+b)$ 를 분배법칙을 이용해 전개하면 다음 공식을 유도 할 수 있다.
$(x+a)(x+b)=x^2+(a+b)x+ab$
계수로 접근하는 방법
$x$에 관한 일차식의 곱으로 표현된 곱셈공식 결과는
$x$에 대한 이차식 ($ax^2+bx+c ,\; a\neq0$)으로 표현되므로
$a,b,c,$ 계수만 계산하여 정리하면 된다.
$(1\cdot x+a)(1\cdot x+b)$
이차항 계수 : (일차항)$\times$(일차항)$=1\times 1$
일차항 계수 : (일차항)$\times$(상수항)$=1\times b +a\times 1$
상수항 계수 : (상수항)$\times$(상수항)$=a \times b$
$(ax+b)(cx+d)$
다음으로 $(ax+b)(cx+d)$를 분배법칙으로 전개하면 다음과 같다.
- $\begin{align}(ax&+b)(cx+d)\\[1em]
&=acx^2+(ad+bc)x+bd\end{align}$
계수로 접근하는 방법
$(a\cdot x+b)(c\cdot x+d)$
이차항 계수 : (일차항)$\times$(일차항)$=a\times c$
일차항 계수 : (일차항)$\times$(상수항)$=(a\times d) +(b\times c)$
상수항 계수 : (상수항)$\times$(상수항)$=b \times d$
암기방법
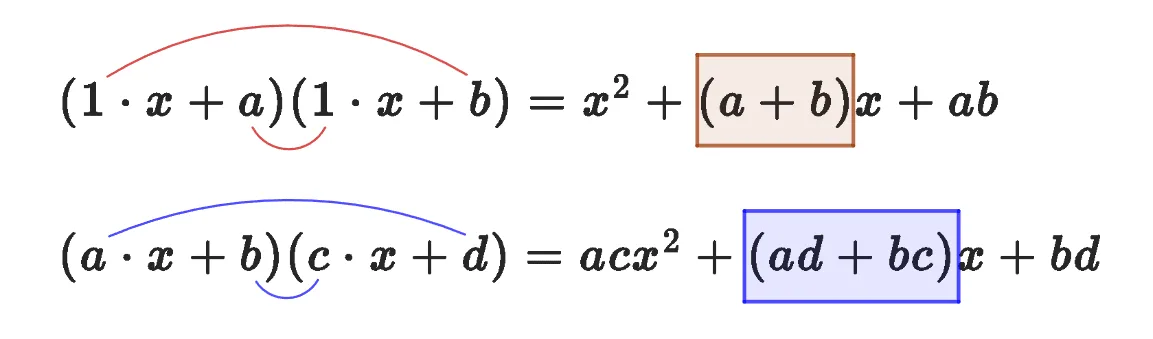
$x$에 대한 일차식이 두 번 곱해진 형태인 경우 암기하는 방법은 다음과 같다.
이차항 : (일차항)$\times$(일차항)
일차항 : (외항곱)$+$(내항곱)
상수항:(상수항)$\times$(상수항)
마무리
곱셈공식을 암기하는 방법은 다양하지만 곱셈공식의 근본적인 구조를 이해하기 위해서는 문자로 암기하는 것보다 언어적인 표현을 익히는 것이 좋다.
문제를 풀면서 곱셈공식을 말로 여러번 반복하여 익숙해 지면 수학의 구조를 통찰할 수 있는 힘이 길러 질 것이다.
이상으로 이번 포스팅을 마무리 하도록 하곘다.
