중학교 곱셈공식에 대한 내용은 간단히 복습하고 고1 곱셈공식에 대한 내용을 학습해 보기로 하자.
목차
[중학교 곱셈공식]
제곱공식
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
합차공식
$(a+b)(a-b)=a^2-b^2$
방정식 공식
$(x+a)(x+b)=x^2+(a+b)x+ab$
$(ax+b)(cx+d)=acx^2+(ad+bc)x+bd$
복습링크
이제 고등학교에서 추가로 배우는 곱셈공식에 대해 학습해 보자.
고1 곱셈공식
중학교에서는 항이 두개이고 제곱식에 관련된 공식을 주로 다룬 반면 고등학교에서는 곱셈공식은 항이 세개이상인 경우와 3차식에 관련된 곱셈공식까지 다룬다.
먼저 곱셈공식 전체를 확인하고 공식에 숨겨진 구조를 하나씩 살펴 보기로 하자.
곱셈공식 정리
중학교 3학년
$(a+b)^2=a^2+2ab+b^2\\[1em]$
$(a-b)^2=a^2-2ab+b^2\\[1em]$
$(a+b)(a-b)=a^2-b^2\\[1em]$
$(x+a)(x+b)=x^2+(a+b)x+ab\\[1.5em]$
$\begin{align}(ax&+b)(cx+d)\\
&=acx^2+(ad+bc)x+bd\end{align}$
고등학교 1학년
$\begin{align}(a+&b+c)^2\\
&=a^2+b^2+c^2+2ab+2bc+2ca\end{align}\\[2em]$
$(a+b)^3=a^3+3a^2b+3ab^2+b^3\\[1em]$
$(a-b)^3=a^3-3a^2b+3ab^2+b^3\\[1em]$
$(a+b)(a^2-ab+b^2)=a^3+b^3\\[1em]$
$(a-b)(a^2+ab+b^2)=a^3-b^3\\[1em]$
$\begin{align}(a+&b+c)(a^2+b^2+c^2-ab-bc-ca)\\
&=a^3+b^3+c^3-3abc\end{align}\\[2em]$
$\begin{align}(a^2&+ab+b^2)(a^2-b+b^2)\\
&=a^4+a^2b^2+b^4\end{align}\\[2em]$
고등학교 곱셈공식 정리
세 항의 제곱공식
$\begin{align}(a+&b+c)^2\\
&=a^2+b^2+c^2+2ab+2bc+2ca\end{align}$
이 공식은 중학교 제곱공식 또는 분배법칙을 이용해 보일 수 있다. 두 방법 모두 수학적으로 중요한 과정이기 때문에 확실히 정리해 두길 바란다.
[제곱공식 이용한 유도]
$\begin{align}(a&+b+c)^2\\[1em]
&=\{(a+b)+c\}^2\\[1em]
&=(a+b)^2+2(a+b)\times c + c^2\\[1em]
&=(a^2+b^2+2ab)+(2ac+2bc)+c^2\\[1em]
&=a^2+b^2+c^2+2ab+2bc+2ca\end{align}$
[분배법칙 이용한 유도]
$\begin{align}(a+b&+c)^2\\[1em]
&=(a+b+c)(a+b+c)\\[1em]
&=\begin{pmatrix}
a^2+ab+ac\\[1em]
+b^2+ba+bc\\[1em]
+c^2+ca+cb
\end{pmatrix}\\[3em]
&=a^2+b^2+c^2+2(ab+bc+ca)\end{align}$
분배법칙을 이용한 풀이는 순열 관련된 아이디어를 포함하고 있다. 다음의 예를 통해 계수를 결정하는 방법에 대해 알아보자.
심화
[다항계수 이용]
주머니 $A, B$ 에 다음과 같이 문자가 하나씩 들어 있을 때
$A=\{a,b,c\},\;B=\{a,b,c\}$ 문자를 하나씩 뽑아 순서대로 배열할 때 나오는 표본을 나열하면 다음과 같고 이를 이용해 계수를 결정할 수 있다. 이는 이항정리와 다항정리를 이해하는 기본적인 아이디어 이다.
$aa, bb, cc$ : $1$개
$ab,ba$: $1$개
$bc,cb$ : $1$개
$ac,ca$ : $1$개
이항정리와 다항정리에 대한 내용은 다음기회에 다루기로 하고 여기서는 다항정리를 적용해 계수만 계산하고 넘어가기로 하자.
다항정리를 이용한 $(a+b+c)^2$의 계수 결정
$a^2 \cdot b^0$ 계수 : $\dfrac{2!}{2! \times 0! \times 0!}=1$
$a^1 \cdot b^1$ 계수 : $\dfrac{2!}{1! \times 1! \times 0!}=2$
암기법
$(a+b+c)^2$을 전개하면 서로 같은 문자끼리 한번씩 곱해지고, 서로 다른 문자$(ab, bc,ca)$는 두번씩 곱해진다.
세제곱 공식
$(a+b)^3=a^3+3a^2b+3ab^2+b^3$
$(a-b)^3=a^3+3a^2b-3ab^2+b^3$
[제곱공식 이용한 유도]
$\begin{align}(a+&b)^3\\[1em]
&=(a+b)^2(a+b)\\[1em]
&=(a^2+2ab+b^2)(a+b)\\[1em]
&=\begin{pmatrix}
a^3+a^2b\\
+2a^2b+2ab^2\\
+ab^2+b^3
\end{pmatrix} \\[1em]
&=a^3+3a^2b+3ab^2+b^3\end{align}$
[$b \rightarrow -b$ 대입]
$(a+b)^3=a^3+3a^2b+3ab^2+b^3$ 식에서 $b \rightarrow -b$를 대입하면 다음 공식을 유도 할 수 있다.
$\begin{align}(a-&b)^3\\[1em]
&=\{a+(-b)\}^3\\[1em]
&=a^3+3a^2(-b)+3a(-b)^2+(-b)^3\\[1em]
&=a^3-3a^2b+3ab^2-b^3\end{align}$
심화과정
[이항정리 이용한 유도]
$(a+b)^3$ 의 전개식의 항별 계수를 구하면 다음과 같고
$a^3 \cdot b^0$ 계수 : $\dfrac{3!}{3! \times 0!}=1$
$a^2b^1$ 계수 : $\dfrac{3!}{2! \times 1!}=3$
$a^1b^2$ 계수 : $\dfrac{3!}{1! \times 2!}=3$
$a^0 \cdot b^3$ 계수 : $\dfrac{3!}{0! \times 3!}=1$
이를 정리하면 $(a+b)^3=a^3+3a^2b+3ab^2+b^3$
을 얻을 수 있다.
암기법
분배법칙을 생각하며 다음과 같이 암기하길 바란다.

세제곱의 합공식, 차공식 $a^3+b^3$
이 공식을 부르는 이름은 따로 존재 하지 않는다. 다만 암기하기 쉽게 하기 위해 제곱의 합차공식과 비슷하므로 세제곱의 합공식, 차공식으로 부르기로 하자.
$(a+b)(a^2-ab+b^2)=a^3+b^3$
$(a-b)(a^2+ab+b^2)=a^3-b^3$
[분배법칙 이용한 유도]
$\begin{align}(a+&b)(a^2-ab+b^2)\\[1em]
&=\begin{pmatrix}
a^3-a^2b+ab^2\\[1em]
+a^2b-ab^2+b^3\\[1em]
\end{pmatrix} \\[2em]
&=a^3+b^3\end{align}$
나머지 식도 동일한 방법으로 보일 수 있다.
$\begin{align}(a-&b)(a^2+ab+b^2)\\[1em]
&=\begin{pmatrix}
\;a^3+a^2b+ab^2\\[1em]
-a^2b-ab^2-b^3\\[1em]
\end{pmatrix} \\[2em]
&=a^3-b^3 \end{align}$
암기법
이 공식은 아래의 그림처럼 도식화 하여 암기하는 것이 효과적이다.

3abc 공식
이 공식도 특징을 따서 3abc공식 이라고 하자. 고등학교 곱셈공식에서 세 항이 곱해진 경우는 이 공식 뿐이므로 문제에서 3abc가 등장한다면 공식을 적용할 생각을 해야 한다.
$\begin{align}(a+&b+c)(a^2+b^2+c^2-ab-bc-ca)\\[1em]
&=a^3+b^3+c^3-3abc\end{align}$
[분배법칙 이용한 유도]
$\begin{align}(a+&b+c)(a^2+b^2+c^2-ab-bc-ca)\\[1em]
&=\begin{pmatrix}
a^3+ab^2+ac^2-a^2b-a^2c-abc\\[1em]
+b^3+a^2b+bc^2-ab^2-b^2c-abc\\[1em]
+c^3+a^2c+b^2c-bc^2-ac^2-abc
\end{pmatrix}\\[3em]
&=a^3+b^3+c^3-3abc\end{align}$
암기법
이 공식을 암기하는 방법은 따로 없다. 단지 계산 과정에서 아래의 파란색 박스 부분이 삭제 됨을 기억하는 것이 암기에 도움이 된다.
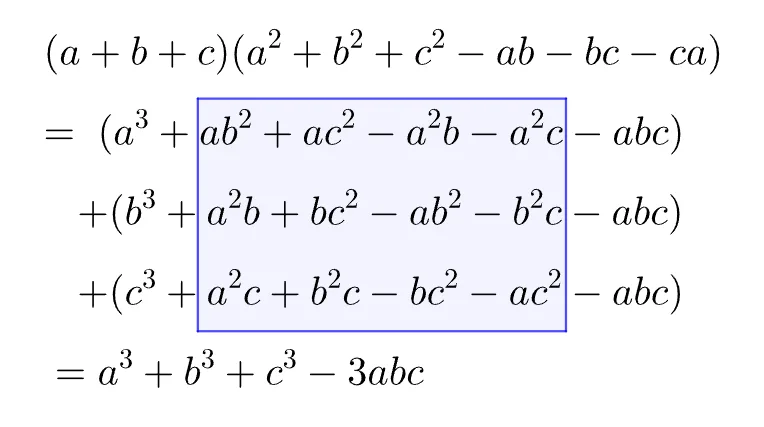
추가공식
곱셈 공식은 아니지만 위의 식과 관련된 식정리 방법에 대해 학습하고 넘어가자.
$\begin{align}a^2&+b^2+c^2-ab-bc-ca\\[1em]
&=\dfrac{1}{2}\{(a-b)^2+(b-c)^2+(c-a)^2\}\end{align}$
$\begin{align}a^2&+b^2+c^2+ab+bc+ca\\[1em]
&=\dfrac{1}{2}\{(a+b)^2+(b+c)^2+(c+a)^2\}\end{align}$
[유도과정]
$\begin{align}a^2&+b^2+c^2-ab-bc-ca\\[1em]
&=\dfrac{1}{2} \times 2(a^2+b^2+c^2-ab-bc-ca)\\[1em]
&=\dfrac{1}{2}(2a^2+2b^2+2c^2-2ab-2bc-2ca)\\[1em]
&=\dfrac{1}{2} \times
\begin{pmatrix}
\; \; a^2+ b^2-2ab\\
+b^2+ c^2-2bc\\
+c^2+ a^2-2ca\\
\end{pmatrix}\\[1em]
&=\dfrac{1}{2}\{(a-b)^2+(b-c)^2+(c-a)^2\}\end{align}\\$
두번 째 식도 비슷하게 보일 수 있다.
$\begin{align}a^2&+b^2+c^2+ab+bc+ca\\[1em]
&=\dfrac{1}{2} \times 2(a^2+b^2+c^2+ab+bc+ca)\\[1em]
&=\dfrac{1}{2}(2a^2+2b^2+2c^2+2ab+2bc+2ca)\\[1em]
&=\dfrac{1}{2} \times
\begin{pmatrix}
a^2+ b^2+2ab\\
+b^2+ c^2+2bc\\
+c^2+ a^2+2ca\\
\end{pmatrix}\\[1em]
&=\dfrac{1}{2}\{(a+b)^2+(b+c)^2+(c+a)^2\}\end{align}$
네제곱의 합차공식
$\begin{align}(a^2&+ab+b^2)(a^2-ab+b^2)\\[1em]
&=a^4+a^2b^2+b^4\end{align}$
[유도과정]
$\begin{align}(a^2&+ab+b^2)(a^2-ab+b^2)\\[1em]
&=\begin{pmatrix}
a^4-a^3b+a^2b^2\\[1em]
+a^3b-a^2b^2+ab^3\\[1em]
+a^2b^2-ab^3+b^4
\end{pmatrix}\\[1em]
&=a^4+a^2b^2+b^4\end{align}$
암기방법
이 공식을 암기하는 방법은 따로 없다. 단지 분배법칙을 이용해 계산과정에서 빨간부분이 삭제 됨을 기억하면 암기에 도움이 된다.
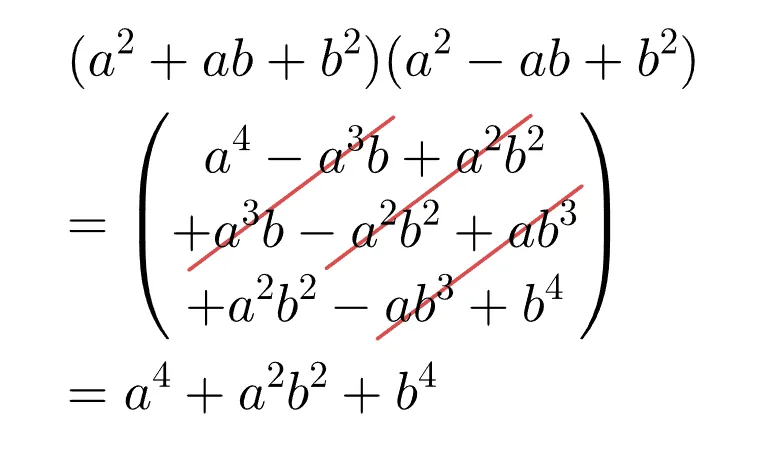
마무리
이번 시간에는 고등학교에서 배우는 곱셈공식을 다양한 관점에서 다루어 보았다. 곱셈공식을 단순히 문자로 암기하는 것 보다 구조에 숨겨진 수학을 발견한다면 더 재미있게 수학을 공부 할 수 있다.
