각 맞꼭지각 수직 거리 정리

각, 맞꼭지각, 수직, 거리의 개념은 도형과 공간의 특징을 이해하는데 중요한 도구이다. 이번 시간에는 이들 용어를 정리하고, 수직과 거리를 체계적으로 정리해 보려고 합니다. 기본 개념을 명확히 이해할 수 있는 시간이 되길 바랍니다.

각 (용어정리)

각 $AOB$

• 각 $AOB$ : $\overrightarrow{OA},\;\overrightarrow{OB}$로 이루어진 도형
• 기호 : $\angle{AOB}$

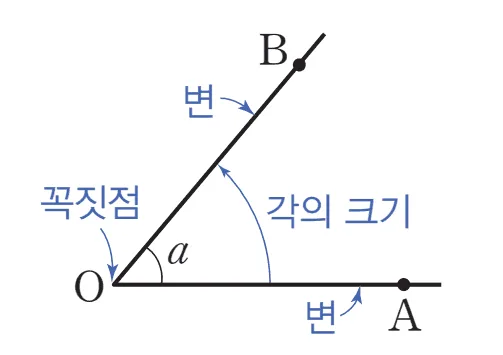
위와 같이 각이 표현된 경우 각은 다음과 같이 다양하게 표현 가능하다.

• $\angle{AOB}=\angle{BOA}=\angle{O}=\angle{a}$

각 $AOB$의 크기

• 각 $AOB$의 크기 : 꼭짓점 $O$를 중심으로 변$OA$가 변 $OB$까지 회전한 양
• 기호 : $\angle{AOB}$
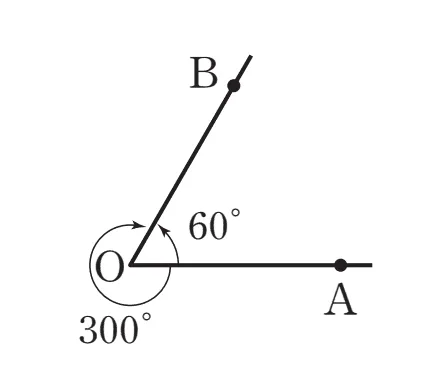
• 오른쪽 그림에서 $\angle{AOB}$의 크기는 $60^\circ$ 또는 $300^\circ$로 생각할 수 있다. 하지만 일반적으로 작은쪽 $60^\circ$를 의미한다.

각의 분류

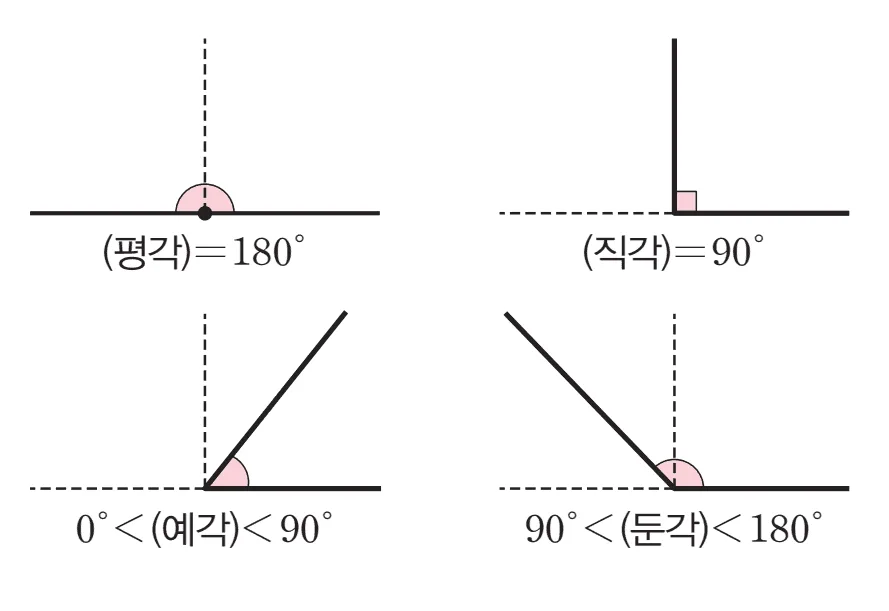
• 평각 : 각의 꼭짓점을 중심으로 정반대로 향하는 두 반직선이 이루는 각.
  • 크기가 $180^\circ$인 각
• 직각 : 평각 크기의 $\dfrac{1}{2}$ 인 각.
  • 크기가 $90^\circ$인 각
• 예각 : $0^\circ<\bbox[#ffff00]{\text{(예각)}}<90^\circ$
• 둔각 : $90^\circ<\bbox[#dcff8c]{\text{(둔각)}}<180^\circ$

교각, 맞꼭지각

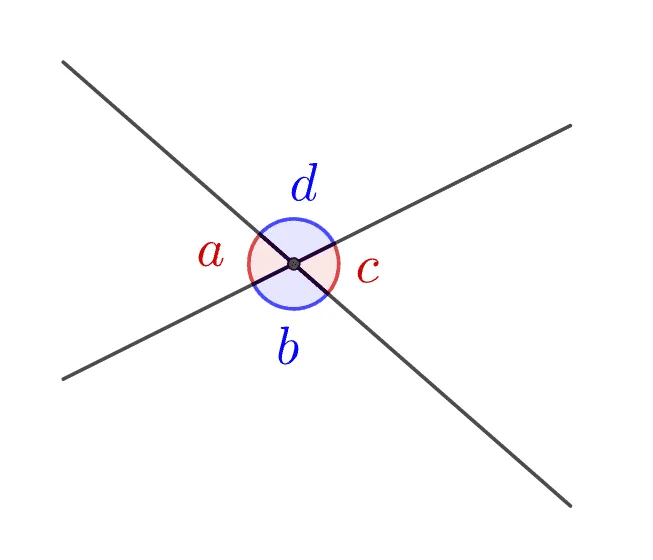
• 교각 : 서로 다른 두 직선이 한 점에서 만날 때 생기는 $\bbox[#ffff00]{\text{네 각}}$
  • $\angle{a},\;\angle{b},\;\angle{c},\;\angle{d}$
• 맞꼭지각 : 교각 중에서 서로 마주 보는 한 쌍의 각
  • $\bbox[#dcff8c]{\angle{a}\text{와 }\angle{c}},\;\bbox[#dcff8c]{\angle{b}\text{와 }\angle{d}}$

맞꼭지각의 성질

• 맞꼭지각의 크기는 서로 같다.
  • $\angle{a}=\angle{c},\; \angle{b}=\angle{d}$

[증명]

$\begin{align}\angle{a}&+\angle{b}=180^\circ,\quad\angle{c}+\angle{b}=180^\circ\\[1em]
\angle{a}&+\angle{b}=\angle{c}+\angle{b}\\[1em]
&\therefore\;\angle{a}=\angle{c}\;\;(\because\;\text{등식의 성질})\end{align}$

비슷한 방법으로 $\angle{b}=\angle{d}$
Q.E.D.

수직

직선과 평면의 수직과 관련된 내용을 다음과 같이 분류하여 체계적으로 정리해 보자.

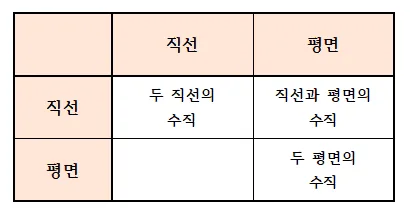
직교 수직 수선

직교의 정의

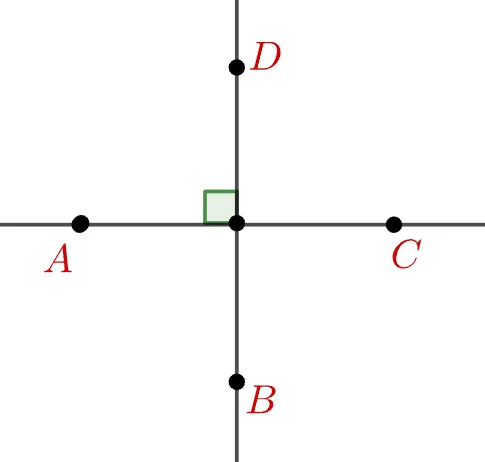
• $\overleftrightarrow{AC},\;\overleftrightarrow{BD}$는 $\bbox[#ffff00]{\text{직교}}$한다 : 두 직선의 교각이 직각($90^\circ$)
  • 기호 : $\overleftrightarrow{AC} \perp \overleftrightarrow{BD}$

선분은 길이가 제한된 직선이기 때문에 만난다는 의미를 포함하는 직교라는 용어대신 수직, 수선이라는 용어를 더 많이 사용한다.

수직의 정의

• $\overleftrightarrow{AC},\;\overleftrightarrow{BD}$ ($\overline{AC},\;\overline{BD}$)에 대하여
  • 두 직선(선분)은 서로 $\bbox[#dcff8c]{\text{수직}}$
    • $\overleftrightarrow{AC} \perp \overleftrightarrow{BD}$ ($\overline{AC} \perp \overline{BD}$)

수선의 정의

• 두 직선이 서로 수직일 때, 한 직선(선분)을 다른 직선(선분)의 $\bbox[#94feff]{\text{수선}}$이라고 한다.

이를 적용하여 위의 그림을 해석하면 다음과 같다.

• $\overleftrightarrow{AC},\;\overleftrightarrow{BD}$는 $\bbox[#ffff00]{\text{직교}}$한다.
• $\overleftrightarrow{AC},\;\overleftrightarrow{BD}$는 $\bbox[#dcff8c]{\text{수직}}$이다.
  • $\overline{AC},\;\overline{BD}$는 $\bbox[#dcff8c]{\text{수직}}$이다.
• $\overleftrightarrow{AC}$는 $\overleftrightarrow{BD}$의 $\bbox[#94feff]{\text{수선}}$이다.
  • $\overline{AC}$는 $\overline{BD}$의 $\bbox[#94feff]{\text{수선}}$이다.

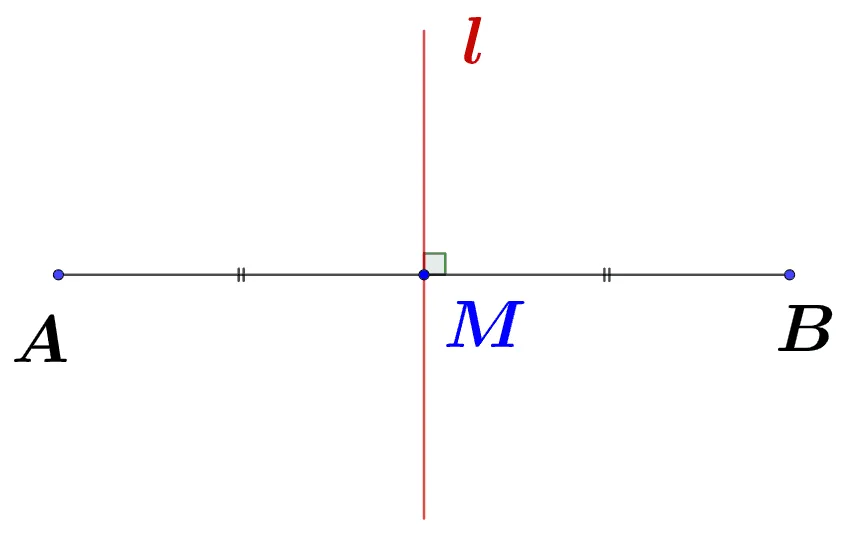
다음으로 수직이등분선에 대해 정리해 보자.

• $l$이 $\overline{AB}$의 수직 이등분선 정의
  • $l$은 $\overline{AB}$의 중점($M$)을 지남
  • $l \perp \overline{AB}$

직선과 평면의 수직

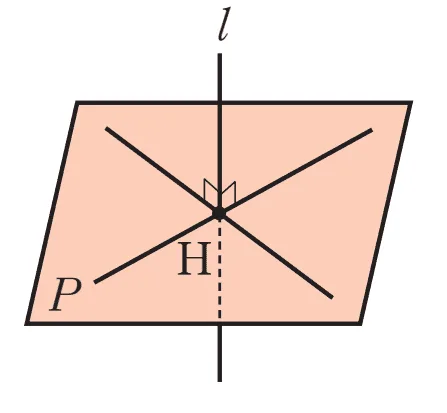
• 직선 $l$과 평면$P$가 수직 : 직선 $l$과 $P$의 교점을 $H$라고 할 때, $H$를 지나는 $P$위의 $\bbox[#ffff00]{\text{모든 직선}}$과 $l$이 수직
  • 기호 : $l\perp P$

위의 조건에서 $\bbox[#ffff00]{\text{모든 직선}}$과 수직임을 확인하기 위한 최소조건은 다음과 같다.

• $H$를 지나는 $P$위의 $\bbox[#ffff00]{\text{모든 직선}}$과 $l$이 수직일 최소 조건
  • $H$를 지나는 $P$위의 $\bbox[#ffff00]{\text{서로 다른 두 직선}}$과 $l$이 수직

위의 사실을 증명하는 과정은 다른 포스팅에서 다루도록 하겠다.

두 평면의 수직

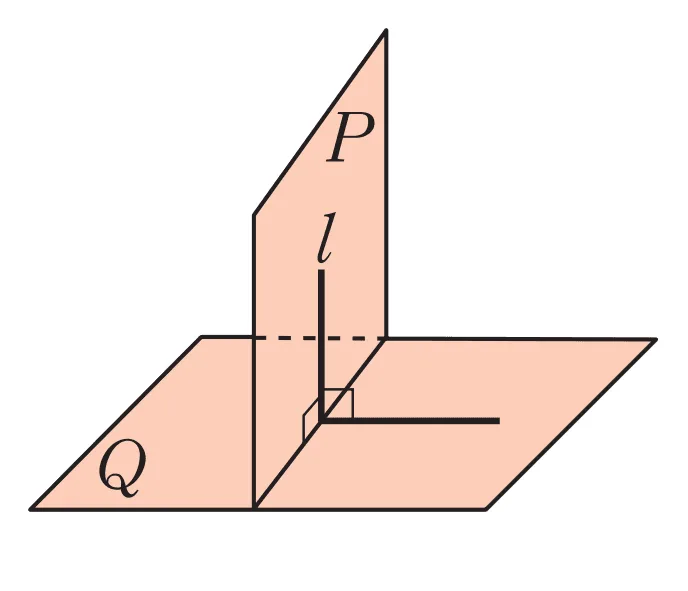
• 평면$P$가 $Q$에 수직 : 평면$P$가 $Q$에 수직인 직선$l$을 포함한다.
  • 기호 : $P\perp Q$

거리

수학에서 거리는 $\bbox[#ffff00]{\text{최단거리}}$를 의미한다. 이 사실을 점과 직선 평면 사이의 거리로 확장해보자.

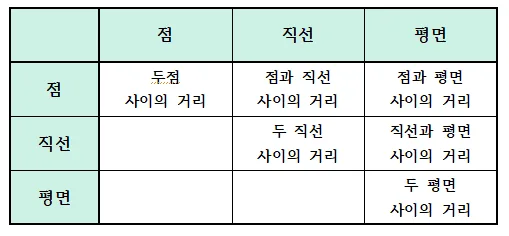
두 점 사이의 거리는 이미 다루었으므로 여기서는 나머지 5가지 경우에 대해 학습해 보자.

점과 직선 사이의 거리

수선의 발

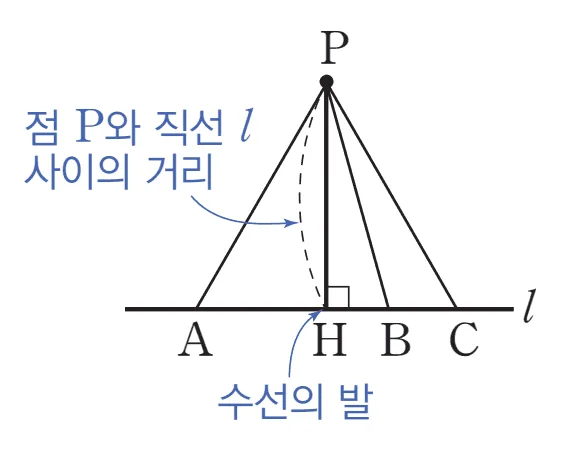
직선 $l$ 위에 있지 않은 점$P$에서 $l$에 수선을 그었을 수선과 $l$의 $\bbox[#dcff8c]{\text{교점(H)}}$을 $\bbox[#dcff8c]{\text{수선의 발}}$ 이라고 한다.

점과 직선 사이의 거리

직선 $l$ 위에 있지 않은 점$P$에서 $l$에 내린 수선의 발$H$에 대하여

• 점 $P$와 직선 $l$ 사이의 거리: $\overline{PH}$

직각 삼각형 $\triangle PAH,\;\triangle PBH,\;\triangle PCH$에서 $\overline{PA},\;\overline{PB},\;\overline{PC}$은 빗변이므로 직각 삼각형의 높이 $\overline{PH}$보다 항상 길다. 따라서 $\overline{PH}$가 $\bbox[#ffff00]{\text{최단거리}}$ 임을 알 수 있다.

점과 평면 사이의 거리

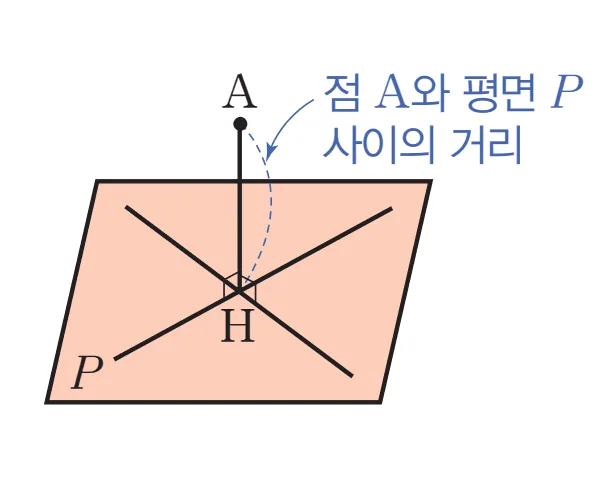
평면 $P$ 위에 있지 않은 점$A$에서 $P$에 수선을 그었을 수선과 $P$의 $\bbox[#dcff8c]{\text{교점(H)}}$을 $\bbox[#dcff8c]{\text{수선의 발}}$ 이라고 한다.

평면 $P$위에 있지 않은 점 $A$에서 $P$에 내린 수선의 발$H$에 대하여

• 점 $A$와 평면 $P$사이의 거리 : $\overline{AH}$

두 직선 사이의 거리 ($l⫽m$)

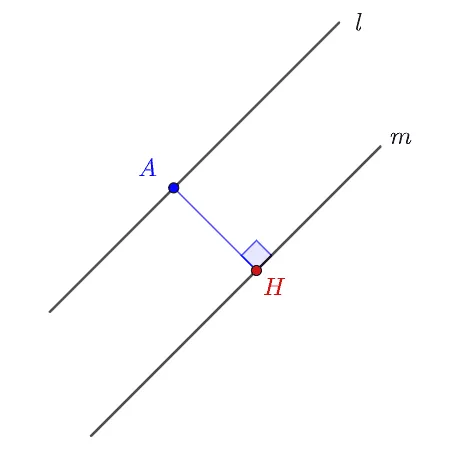
서로 다른 평행한 두 직선 $l,\;m$에 대하여 $l$위의 점 $A$에서 직선 $m$에 내린 수선의 발을 $H$라고 할 때

• 두 직선 $l,\;m$사이의 거리 : $\overline{AH}$

직선과 평면 사이의 거리 ($l⫽P$)

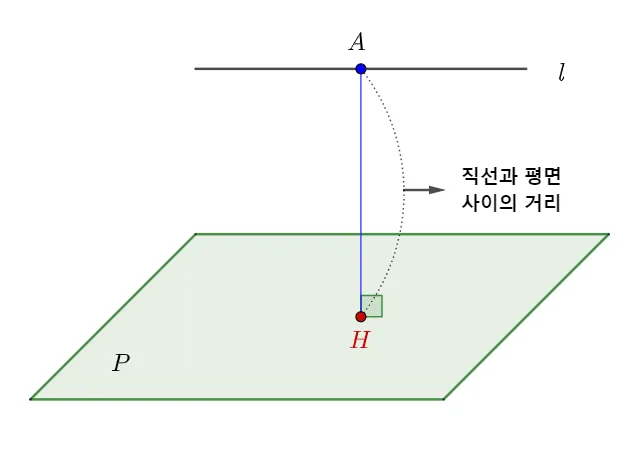
서로 평행한 직선$l$ 과 평면 $P$에 대하여 $l$위의 점 $A$에서 평면 $P$에 내린 수선의 발을 $H$라고 할 때

• 직선 $l$과 평면 $P$사이의 거리 : $\overline{AH}$

두 평면 사이의 거리 ($P⫽Q$)

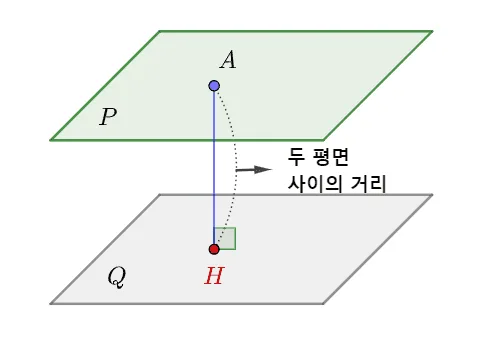
서로 평행한 평면 $P,\;Q$에 대하여 평면 $P$위의 점 $A$에서 평면 $Q$에 내린 수선의 발을 $H$라고 할 때

• 두 평면 $P,\; Q$사이의 거리 : $\overline{AH}$

맺음말

수직과 거리의 개념은 일상에서 사용하는 용어와 달리 수학에서는 명확히 정의하여 엄밀하게 사용된다. 이들 개념을 정확하게 이해하고 기하적 사고의 기초 다지길 바란다.