일차함수의 그래프 추정, 위치관계 판정

일차함수의 그래프는 단 두 가지 정보 기울기와 절편의 부호 만으로도 개형을 빠르게 예측할 수 있습니다. 이 글에서는 일차함수의 그래프를 어떻게 기울기와 절편을 기준으로 추정할 수 있는지, 그리고 두 일차함수의 위치관계를 어떻게 판정하는지를 직관적으로 설명합니다.

일차함수의 그래프, 기울기, 절편(복습)

$y=ax+b$ 그래프

$y=ax+b,\;(a\neq0)$의 그래프는 $y=ax$의 그래프를 위쪽으로 평행이동한 그래프이고, 다음과 같이 학습하였습니다.

• $y=ax\xrightarrow[]{\bbox[#ffff00]{y}\text{축} \bbox[#dcff8c]{b} \text{만큼 평행이동}}y=ax+\bbox[#ffff00]{b}$ ($a\neq0$)

$y=ax+b$ 기울기와 절편

일차함수의 일반형 $y=\bbox[#ffff00]{a}x+\bbox[#dcff8c]{b},\; (a\neq0)$의 기울기와 절편을 다음과 같이 학습 하였습니다.

1. $\bbox[#ffff00]{\text{기울기}}$: $\dfrac{y\text{값의 증가량}}{x\text{값의 증가량}}=\bbox[#ffff00]{a}$
2. 절편
   • $\bbox[#dcff8c]{y \text{ 절편}}$: $\bbox[#dcff8c]{b}$ ($x=0$ 일 때 $y$값)
   • $x$ 절편: $-\dfrac{b}{a}$ ($y=0$ 일 때 $x$값)

기울기 절편으로 그래프 추정

$y=\bbox[#ffff00]{a}x+\bbox[#dcff8c]{b},\;(a\neq0)$의 그래프는 기울기와 절편을 이용해 다음과 같이 추정해 볼 수 있습니다.

1. $\bbox[#ffff00]{a}$: 기울기
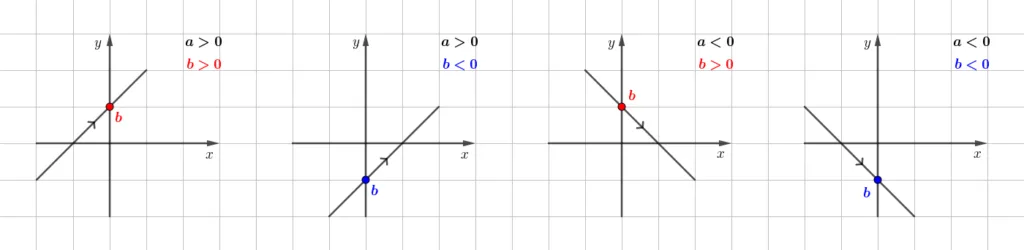
   • $a>0$: $x$가 증가할 때 $y$도 증가 $\rightarrow$오른쪽 위로 향하는 직선
   • $a<0$: $x$가 증가할 때 $y$가 감소 $\rightarrow$오른쪽 아래로 향하는 직선
   • $\left | a\right |$이 클수록 $y$축에 가까워 진다.
   • $\left | a\right |$이 작을 수록 $x$축에 가까워 진다.
2. $\bbox[#dcff8c]{b}$: $y$ 절편
   • $b=0$: 원점을 지난다.(정비례)
   • $b>0$: $y$절편이 양수 $\rightarrow$ $y$축 위쪽에서 만난다.
   • $b<0$: $y$절편이 음수 $\rightarrow$ $y$축 아래쪽에서 만난다.

위의 사실을 종합하면 그래프 개형을 다음과 같이 추측할 수 있습니다.

두 일차함수의 위치관계 판정

일차함수의 그래프는 좌표평면상의 직선이기 때문에 일차함수의 위치관계는 평면에서의 직선의 위치관계와 같습니다. 따라서 다음 세 위치관계로 나누어 살펴 볼 수 있습니다.

1. 한 점에서 만난다.
2. 평행하다.
3. 일치한다.

위치관계 판정법

두 일차함수 $y=ax+b,\;y=a’x+b’$의 위치관계를 관계식을 이용해 판정하는 방법은 다음과 같습니다.

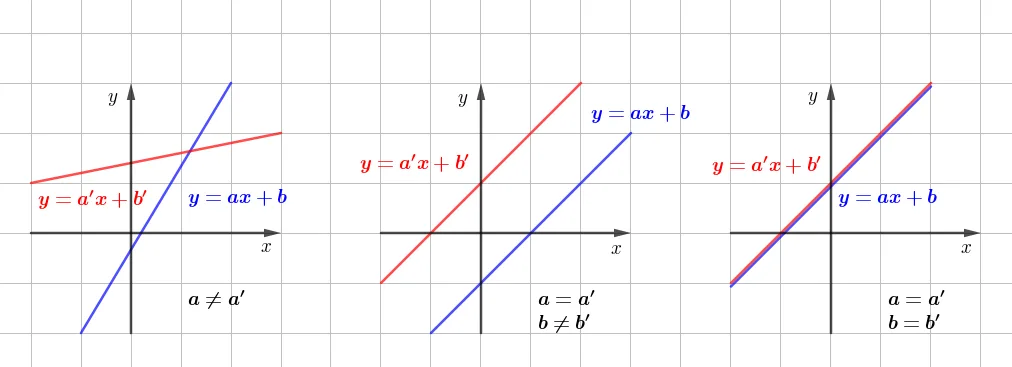
기울기($a$)가 다르면 두 직선은 한 점에서 만나고, 기울기가 같은($a=a’$) 두 직선은 평행하거나 일치한다.

1. 한 점에서 만날 조건: $a \neq a’$ (기울기)
2. 평행한 조건: $a=a’$ (기울기), $b\neq b’$ ($y$절편)
3. 일치할 조건: $a=a’$ (기울기), $b=b’$ ($y$절편)