합의 법칙과 곱의 법칙을 이용해 경우의 수를 계산하는 과정은 수학적 확률을 계산하는데 있어 기본이 된다. 각 용어에 대한 정확한 정의를 토대로 곱의 법칙의 개념을 정확히 이해하길 바란다.
목차
용어정의
- 시행 : 동일한 조건을 가지고 반복가능한 실험
- 표본공간 ($S$) : 시행을 통해 일어날 수 있는 모든 결과
- 사건 : 시행의 결과 일어날 수 있는 event
- 경우의 수 : 시행의 결과 일어날 수 있는 사건의 가짓 수
[예시]
- 시행 : 정육면체 주사위를 던지는 실험
- 표본공간 : $S=\{1,2,3,4,5,6\}$
- 사건 A : 짝수 눈이 나오는 사건
$A=\{2,4,6\}$
사건 B : 3의 배수 눈이 나오는 사건
$B=\{3,6\}$ - 짝수 눈이 나오는 경우의 수 : $n(A)=3$
3의 배수 눈이 나오는 경우의 수 : $n(B)=2$
[정리] 합의 법칙 (경우의 수)
위의 기호를 이용해 합의 법칙을 정리하면 다음과 같다.
어떤 시행을 통해 발생한 사건 $A, B$에 대하여 A 또는 B가 일어날 경우의 수$n(A \cup B )$는 다음과 같다.
- $n(A \cup B )=n(A)+n(B)-n(A \cap B)$
합의 법칙은 포함배제의 원리와 밀접하게 관련되어 있고 다룰 내용이 많다 따로 포스팅 하였으니 추가 학습이 필요하면 아래의 링크를 이용해 학습하길 바란다.
곱의 법칙 예제
곱의 법칙은 중학교 2학년에 처음 등장하는 개념이므로 간단한 예제를 통해 복습하고 학습을 이어가도록 하자.
[예제] 다음은 $A$에서 $C$까지 길을 선으로 연결한 그림이다. $A$에서 $C$로 가는 경우의 수를 구하여라.
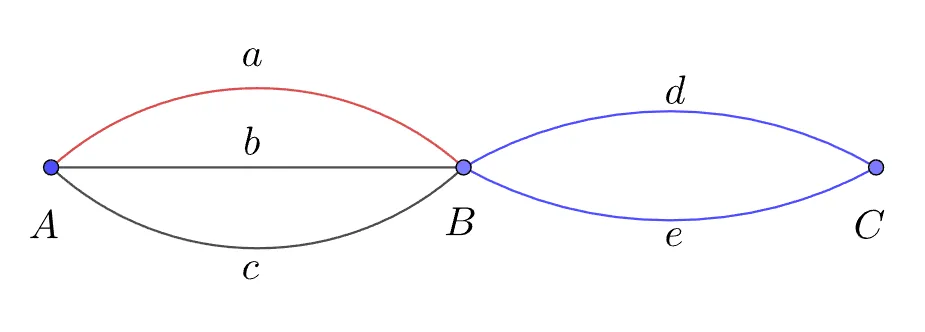
사건$P, Q, R$ 를 각각 $a,b,c$를 통해 C로 가는 사건이라 하자
$P$ : $a\rightarrow d$ 또는 $a\rightarrow e$ 2가지
$Q$ : $b\rightarrow d$ 또는 $b\rightarrow e$ 2가지
$R$ : $c\rightarrow d$ 또는 $c\rightarrow e$ 2가지
$P,Q,R$에 합의 법칙을 적용하면 다음과 같다.
$A \rightarrow C$ 의 경우의 수
$=n(P \cup Q \cup R)\;\;(\because\; 합의 법칙)$
$=n(P)+n(Q)+n(R)\;\;(\because [교집합]=\phi)$
$=3 \times 2$
$=(A \rightarrow B인\;경우의 \;수) \times (B \rightarrow C인 \;경우의 \;수)$
($A \rightarrow C$ 경우의 수)은 ($A \rightarrow B$ 경우의 수)와 ($B \rightarrow C$ 경우의 수)를 곱하여 계산할 수 있음을 알 수 있다.
이처럼 두 사건이 연달아 일어나거나 동시에 일어난 경우의 수를 구할 때 사용할 수 있는 법칙을 곱의 법칙이라고 하고 아래와 같이 정리할 수 있다.
[정리] 곱의 법칙
두 사건 $A, B$가 서로 영향을 주지 않은 채로 동시에 또는 연달아 일어나야 하는 사건의 경우의 수 $n(A \cap B)$는 다음과 같다.
- $n(A \cap B)=n(A) \times n(B)$
$A, B$ : 서로 영향을 주지 않고 발생하는 사건
$A \cap B$ : 동시에 또는 연달아 일어나는 사건
위의 조건을 만족하면 세 사건에 대해서도 다음이 성립한다.
- $n(A \cap B \cap C)=n(A) \times n(B) \times n(C)$
곱의 법칙 확장
곱의 법칙은 순서쌍 집합 $\{(a,b)| a \in A, b \in B \}=A \times B $의 원소의 개수를 구할 때 사용할 수 있다.
- $| A \times B | = |A| \times |B|$
세 집합의 순서쌍의 원소 개수에 대해서도 정리하면 다음과 같다.
- $| A \times B \times C | = |A| \times |B| \times |C|$
$A \times B \times C=\{(a,b,c)| a \in A, b \in B, c \in C \}$
곱의 법칙 문제풀이
중학교 고등학교에서 이용되는 곱의 법칙에 대한 전형적인 문제에 대해 살펴보고 학습을 마무리 하도록 하자.
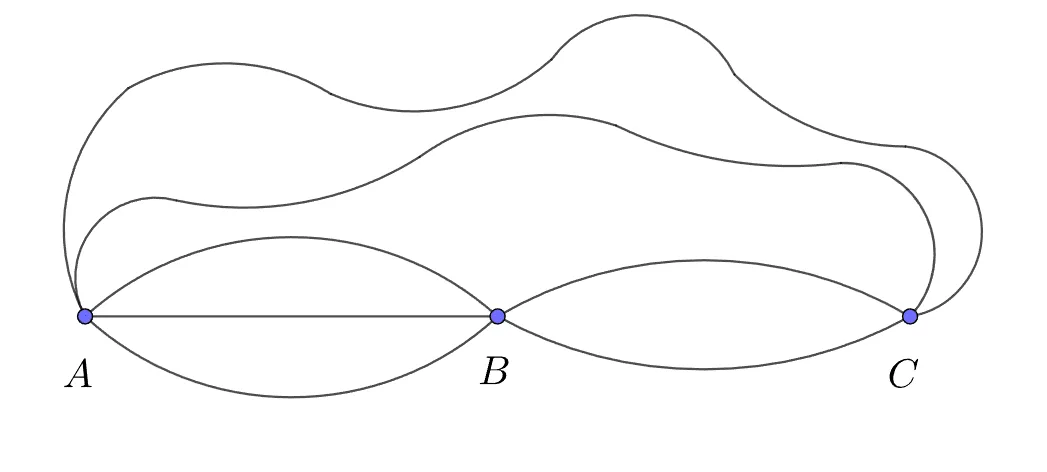
[문제1] $A$ 에서 $C$ 로 가는 길의 경우의 수를 구하여라
[풀이]
사건$P$ : $B$를 거치지 않고 $A \rightarrow C$
$n(P)=2$가지
사건 $Q$ : $A \rightarrow B \rightarrow C$
$n(Q)=3 \times 2=6$가지 $(\because\; 곱의 법칙)$
$\therefore\;[A \rightarrow C\; 경우의 \;수\;]=n(P)+n(Q)$
$=2+6=8\;(\because\;합의\;법칙)$
[문제2] 자연수 $n$이 다음과 같이 소인수 분해 될 때 약수의 개수를 구하여라.
$$n=p^a \times q^b \times r^c\;\;(p,q,r:서로\;다른\;소수)$$
[풀이]
$n$의 약수 집합 : $N=\{p^i q^j r^k | 0 \leq i \leq a,\; 0 \leq j \leq b,\;0 \leq k \leq c\;(i,j,k:정수)\}$
집합N의 원소는 $i,j,k$에 의해 결정 되므로 $i,j,k$에 들어갈 수 있는 정수의 개수에 의해 $N$의 원소의 개수도 결정된다.
$i \rightarrow 0,1,\cdots,a$
$j \rightarrow 0,1,\cdots,b$
$k \rightarrow 0,1,\cdots,c$ 이고,
$i,j,k$는 동시에 한 가지씩 결정되어야 약수가 하나 결정되므로 곱의 법칙을 적용하여 경우의 수를 계산하면 다음과 같다.
$\therefore\;[n의\;약수의\;개수]=(a+1) \times (b+1) \times (c+1)$
[문제3] 집합 $X=\{1,2,3,4\}$ 에서 집합 $Y=\{1,2\}$로 가는 모든 함수의 개수를 구하여라.
[풀이]
$f:X\rightarrow Y$ : $X$의 원소마다 $Y$값에 오직 하나씩 대응 되는 관계
사건 $A,B,C,D$를 각 각 $1,2,3,4$가 가질 수 있는 함숫값이라 하자.
$f(1)=1$ 또는 $f(1)=2$ 이므로 $n(A)=2$ 이고
비슷한 방법으로 $n(B)=2,\;n(C)=2,\; n(D)=2$임을 알 수 있다.
사건 $A,B,C,D$가 동시에 일어나야 함수를 하나 만들수 있으므로 곱의 법칙을 적용해 함수의 개수를 구하면 다음과 같다.
$\therefore\; n(A)\times n(B)\times n(C)\times n(D)=8개$
[문제4] 집합 $A=\{1,2,3,\cdots,n\}$ 의 부분집합의 개수가 $2^n$임을 보여라.
[풀이]
사건 $A_{K}$를 부분집합을 만들때 원소 $k$ 를 사용할 수 있는 방법이라고 하자.
사건 $A_{1}$ : 부분집합을 만들때 원소 1를 사용할 수 있는 방법
- 1 을 부분집합에 포함 시키는 방법
- 1 을 부분집합에 포함 시키지 않는 방법
따라서 사건 $A_{1}$의 경우의 수는 $2$가지 이고 비슷한 방법으로 $A_{2},\cdots ,A_{n}$의 모든 경우의 수는 $2$ 가지이다.
$A$의 각 원소 마다 사건 $A_{k}$를 동시에 고려해야 부분집합을 하나를 만들 수 있다. 따라서 곱의 법칙을 적용하면 집합$A$의 부분집합의 개수는 $2^n$ (개)이다.
마무리
곱의 법칙은 합의 법칙과 함께 수학에서 개수를 헤아리는 가장 기본적인 방법이다. 이 두가지 법칙은 각 단원에서 따로 접하면 너무 당연하고 쉽게 다가오기 때문에 정확히 정리하지 않고 넘어가기 쉽다. 이 문제점은 나중에 고등학교 순열과 조합을 이용해 복잡한 상황의 경우의 수를 헤아리는 과정에서 드러난다.
이번 기회에 합의 법칙과 곱의 법칙을 잘 정리해서 복잡한 상황에서도 규칙을 잘 적용할 수 있기를 바란다.
